Класифікація коригувальних кодів

З деякими коригуючими кодами студенти вже знайомі за матеріалами, наведеними в лабораторній роботі №5. Наведемо основні положення, що стосуються саме циклічних кодів.

Всі коригувальні коди можна розділити на два класи: блокові і безперервні.

Блокові коди - коди, в яких кожному повідомленню (або елементу) ставиться у відповідність блок з n символів (кодовий вектор довжиною n). Операції кодування та декодування в кожному блоці робляться окремо.

Безперервні коди являють собою безперервну послідовність символів, що не підрозділяється на блоки. Такі коди називаються також рекурентними, ланцюговими, зверточними, конволюційними. Процеси кодування і декодування здійснюються безперервно. Передана послідовність утворюється шляхом розміщення в певному порядку перевірочних символів між інформаційними символами вихідної послідовності.

Як блокові, так і безперервні коди діляться на роздільні та нероздільні.

Роздільні коди передбачають можливість чіткого розмежування інформаційних і перевірочних символів.

Нероздільні коди не передбачають такої можливості і до них відносяться, наприклад, коди з постійним вагою (КПВ).

Роздільні коди поділяються, у свою чергу, на систематичні (лінійні або групові) і несистематичні (нелінійні).

Систематичні коди характеризуються тим, що сума за модулем двох дозволених кодових комбінацій кодів цього класу знову дає дозволену кодову комбінацію.

Крім того, в систематичних кодах інформаційні символи, як правило, не змінюються при кодуванні і займають певні наперед задані місця. Перевірочні символи обчислюються як лінійна комбінація інформаційних, звідки і виникла інше найменування цих кодів - лінійні. Для систематичних кодів приймається позначення [n, k] - код, де k - число інформаційних символів в кодової комбінації, n - загальне число символів в коді.

Несистематичні коди не володіють зазначеними вище властивостями і застосовуються значно рідше, ніж систематичні, зокрема, в несиметричних каналах зв'язку.

Циклічні коди складають велику групу найбільш використовуваних на практиці лінійних, систематичних кодів. Їх основна властивість, що дало їм назву, полягає в тому, що кожен вектор, одержуваний з вихідного кодового вектора шляхом циклічної перестановки його символів, також є дозволеним кодовим вектором. Прийнято описувати циклічні коди (ЦК) за допомогою породжують полиномов G (Х) ступеня r = n - k, де r - число перевірочних символів в кодовому слові.

У зв'язку з цим циклічні коди відносяться до різновиду поліноміальних кодів.

Циклічні коди широко застосовуються при побудові пристроїв обчислювальної техніки та обчислювальних мереж.

Визначимо деякі поняття, що зустрічаються при використанні циклічних кодів.

CRC (Cyclic redundancy check) - код циклічного контролю. Термін використовується тільки для завадостійких циклічних кодів, що виявляють помилки. Літерами CRC також вказуються розряди (байти), що відводяться під контрольні (надлишкові) символи, що формуються при передачі (записи). При прийомі (читанні) за допомогою цих символів визначається відсутність або наявність помилки.

EDC (Error Diagnostic Codes) - завадостійкі коди, що виявляють помилки. Термін використовується для всіх завадостійких кодів, що виявляють помилки. Літерами EDC також вказуються розряди (байти), що відводяться у форматі під контрольні символи, що формуються при передачі (запису) інформації. При прийомі (читанні) за допомогою цих символів визначається наявність або відсутність помилки.

ECC (Error Correction Codes) - завадостійкі коди, що виправляють помилки. Літерами ECC вказуються також розряди (байти), що відводяться для контрольних символів, формованих при передачі (запису). При прийомі (читанні) за допомогою цих символів визначається наявність помилки і проводиться виправлення.

При використанні циклічних кодів всі контрольні символи прийнято розміщувати в кінці кодової комбінації після інформаційних символів.

Наведемо деякі приклади застосування циклічних кодів.

У накопичувачах на гнучких магнітних дисках всі операції запису даних супроводжуються формуванням і записом в кінці поля після 512 інформаційних байт (сектор) 2 байт CRC.

У накопичувачах на жорстких магнітних дисках (НЖМД) використовуються циклічні коди, що виправляють помилки (ECC). Фірми-виробники НЖДМ включають схеми формування ECC і виправлення помилок у контролери жорстких дисків. Оскільки в даний час використовуються НЖДМ з вбудованими контролерами, то користувачеві і не повідомляється про конкретний використовуваному коді. Наприклад, у ряді контролерів для сектора довжиною 512 байт формується ECC довжиною 7 байт.

У CD-ROM для забезпечення високої надійності в формат файлової системи за стандартом ISO 9660 (High Sierra) введені поля EDC довжиною 4 байта і ECC довжиною 276 байт для інформаційного поля довжиною 2048 байт. Використовується код Ріда-Соломона з перемеженіем- CIRS-Cross Interleave Reed Solomon. Цей же код використовується в ряді пристроїв архівного зберігання інформації на магнітній стрічці (стримерах).

В універсальній послідовній шині USB-Universal Serial Bus - для виявлення помилок передачі кожен пакет має поля CRC, що дозволяють виявляти всі одноразові і дворазовий бітові помилки.

Операції кодування та декодування ЦК зводяться до відомих процедур множення і ділення поліномів. Для двійкових кодів ці операції легко реалізуються технічно за допомогою лінійних переключательних схем (ЛПС), при цьому виходять відносно прості схеми кодеків, в чому полягає одна з практичних достоїнств ЦК.

Циклічний код передбачає послідовну обробку розрядів кодового слова, що зручно для передачі даних по одній лінії зв'язку. Він легко реалізується технічно за допомогою регістрів зсуву зі зворотними зв'язками й широко застосовується як у системах передачі даних, так і при контролі інформації на внутрішньому запам’ятовуючому пристрої (ВЗП). У циклічному коді для виявлення помилок використовується властивість всіх його кодових слів: при поданні їх у вигляді поліномів ділиться націло на утворюючий поліном, від властивостей якого й залежать характеристики коду. Так, для коду 7,4 можуть застосовуватися утворені поліноми виду х³+ х + 1 або х³+ х² + 1, при цьому D_min = 3. Як надлишкові розряди й ознаки помилки використовується залишок від розподілу кодового полінома на утворюючий. У системах передачі даних найчастіше застосовуються утворюючі поліноми виду х¹⁶ + х¹² + х⁵ + 1, яким відповідають 16 надлишкових розрядів.

Математичний апарат розподілу багаточленів легко реалізується за рахунок використання регістрів зрушення зі зворотними зв'язками. Простота апаратної реалізації і висока коригувальна здатність коду (наприклад, код з перевірочним багаточленом 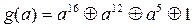забезпечує виявлення 99,999% помилок) визначили надзвичайно високе поширення циклічного коду: він використовується, наприклад, у мережах передачі даних, при записі на магнітні й оптичні диски.

Серед циклічних кодів особливе місце займає клас кодів, запропонованих Боузом і Чоудхурі і незалежно від них Хоквінгемом. Коди Боуза-Чоудхурі-Хоквінгема отримали скорочене найменування БЧХ-коди. БЧХ-коди є узагальненням кодів Хеммінга на випадок виправлення декількох незалежних помилок. Окремими випадками БЧХ-кодів є коди Файра, призначені для виявлення та виправлення серійних помилок ("пачок" помилок), код Голея - код, що виправляє одиночні, подвійні і потрійні помилки (D_min = 7), коди Ріда-Соломона.

Коди Боуза-Чоудхурі-Хоквінгема (БЧХ) - клас циклічних кодів, що виправляють кратні помилки, тобто дві і більше (d₀³ 5).

Теоретично коди БЧХ можуть виправляти довільну кількість помилок, але при цьому істотно збільшується тривалість кодової комбінації, що призводить до зменшення швидкості передачі даних і ускладнення приймально-передавальної апаратури (схем кодерів і декодерів).

Математичний апарат розподілу багаточленів легко реалізується за рахунок использование регістрів зрушення зі зворотнього зв'язку. Простота апаратної реализации и висока коригувальна здатність коду (наприклад, код з перевірочнім багаточленом 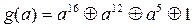забезпечує виявлення 99,999% помилок) визначили надзвичайно високе поширення ціклічного кодом: Він вікорістовується, наприклад, у мережа передачі даних, при запісі на магнітні й оптичні диски.

Коди Ріда-Соломона - недвійкові систематичні лінійні блокові коди, які відносяться до класу циклічних кодів, і які є підмножиною кодів Боуза-Чоудхурі-Хоквінгема. Коригувальні здатності кодів Ріда-Соломона. безпосередньо залежать від кількості контрольних байт.

Додавання r контрольних байт дозволяє виявляти r довільним чином перекручених байт, гарантовано відновлюючи r / 2 байт з них.

Порядок виконання роботи

1. Завантажити програму Sourse (IPK).

2. Ознайомитись з панеллю програми.

3. Виконати кодування циклічним кодом з використанням утворюючого полінома х³ + х + 1 та х³ + х²+ 1.

4. Результати занести в таблицю.

5. Проаналізувати результати.

6. Завантажити програму RSCODEC.

7. Ознайомитись з панеллю програми.

8. Виконати кодування кодом Ріда-Соломона. Результати занести в таблицю.

9. Проаналізувати результати.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Дані для кодування	\|

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.019 сек.