• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Парадокс Рассела

Завдання|задавання| множин|безлічі| характеристичним предикатом може приводити|призводити,наводити| до суперечностей|протиріч|. Наприклад, всі розглянуті|розгледіти| в прикладах|зразках| множини|безліч| не містять|утримують| себе як елемент. Розглянемо|розгледимо| безліч всіх множин|безлічі|, що не містять|утримують| себе як елемент: .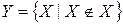

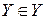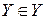Якщо множина|безліч| існує, то ми повинні мати можливість|спроможність| відповісти на наступне|таке| питання: ? Хай |нехай|, тоді . Хай |нехай|, тоді 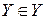. Виходить неусувна логічна суперечність|протиріччя|, яка відома як парадокс Рассела. Існує три способи уникнути цього парадоксу.

1. Обмежити використовувані характеристичні предикати виглядом|видом|

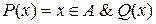
де 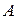– відома, свідомо існуюча множина|безліч| (універсум). Звичайно при цьому використовують позначенн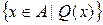я . Для універсум не вказаний, а тому множиною|безліччю| не є|з'являється,являється|.

2. Теорія типів. Об'єкти мають тип 0, множини|безліч| мають тип 1, безліч множин|безлічі| – тип 2 і т.д. не має типу і множиною|безліччю| не є|з'являється,являється|.

3. Характеристичний предикат 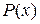заданий у вигляді обчислюваної|обчисляти,вичисляти| функції (алгоритму). Спосіб обчислення|підрахунку| значення предиката 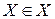не заданий, а тому множиною|безліччю| не є|з'являється,являється|.

Останній з|із| перерахованих способів лежить в основі так званого конструктивізму – напряму|направлення| в математиці, в рамках|у рамках| якого розглядаються|розглядуються| тільки|лише| такі об'єкти, для яких відомі процедури (алгоритми) їх породження. У конструктивній математиці виключаються з|із| розгляду деякі поняття і методи класичної математики, чреваті можливими парадоксами.

3.3. Порівняння множин|безлічі|

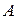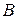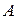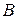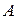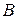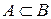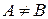Множина|безліч| міститься|утримується| в множині |безлічі|, якщо кожен елемент є елемент . Записується|занотовується| це наступним|слідуючим| способом: . В цьому випадку називається підмножиною . Якщо і , то 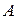називається власною підмножиною .

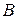Потужність множини|безлічі| 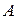позначається|значиться| як 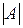. Для кінцевих|скінченних| множин|безлічі| потужність – це число елементів. Наприклад, 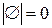, але|та| 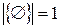. Якщо 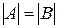, то множини|безліч| 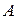і 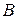називаються рівнопотужними.

Іноді|інколи| в літературі замість потужності множини|безлічі| використовується інший рівнозначний йому термін: кардинальне число множини|безлічі| (від латинського cardinalis – головний). Цей термін був введений|запроваджений| Георгом Кантором.

3.4. Операції над множинами|безліччю|

Звичайно розглядаються|розглядуються| наступні|слідуючі| операції над множинами|безліччю|:

· Об'єднання: .

· Перетин: .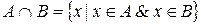

· Різниця: .

· Симетрична різниця:

.

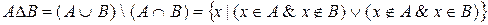· Доповнення: .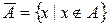

Операція доповнення має на увазі деякий універсум:

.

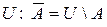· Декартові добич|добуток| множин|безлічі|:

.

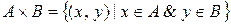Декартові добич|добуток| двох множин|безліч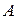і| і 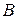є безліч всіх впорядкованих пар (x, у|в,біля|), де і .

Приклад|зразок| 3.2. Хай|нехай| ,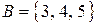. Тоді

, , , .

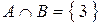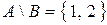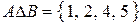На мал. 3.1 приведені діаграми Ейлера, що ілюструють операції над множинами|безліччю|. Самі початкові|вихідні| множини|безліч| зображаються|змальовуються| геометричними фігурами (нескінченна|безконечна| безліч крапок|точок| на площині|плоскості|), результат виділяється за допомогою штрихування.

Мал. 3.1. Діаграми Ейлера

3.5. Властивості операцій над множинами|безліччю|

Хай|нехай| заданий універсум 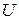. Тоді 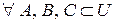виконуються наступні|такі| властивості.

1. Інволютівность:

;

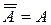2. Ідемпотентність:

, ;

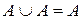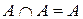3. Комутативність:

, ;

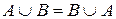4. Асоціативність:

, ;

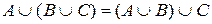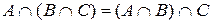5. Дистрибутивність:

, ;

6. Поглинання:

, ;

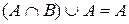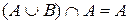7. Властивість нуля:

, ;

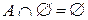8. Властивість одиниці:

, ;

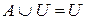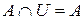9. Закони де| Моргана:

, ;

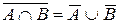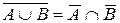10. Властивості доповнення:

, ;

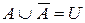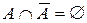11. Вираз|вираження| для різниці:

.

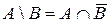Читайте також:

1. Астросоціологічний парадокс
2. Головний «етичний парадокс» психології
3. Ефект доходу та ефект заміщення. Парадокс Гіффена
4. ПАРАДОКС ЗАОЩАДЖЕННЯ.
5. Парадокс заощадження.
6. Парадокс Леонтьєва та його пояснення
7. Парадокс Леонтьєва” та його пояснення.
8. Парадокси і софізми
9. Парадокси теорії множин
10. Турбота як властивість розуму та її гіпотетична роль у ситуації астросоціологічного парадокса

Переглядів: 825