• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Проблема континууму

Булеан

Безліч всіх підмножин множини|безлічі| 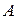називається булеаном|.

Теорема 3.1. Множина|безліч| з|із| n елементів має підмножин.

Доказ: Цю теорему можна довести різними способами (так само, як і багато інших теорем). Ми доведемо її, використовуючи бінарні представлення чисел. Припустимо|передбачимо|, що ми маємо множину|безліч| з|із| трьох елементів 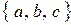. Кожну підмножину цієї множини|безлічі| зашифруємо за допомогою бінарного коду. Цей код складатиметься з трьох біт (по кількості членів початкової|вихідної| множини|безлічі|). Якщо в даній підмножині присутній елемент , першому біту коду привласнюємо значення одиниці, інакше – нуля. Якщо в підмножині присутній елемент 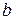, другому біту привласнюємо значення одиниці, інакше – нуля. Якщо в підмножині присутній елемент 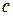, третьому біту привласнюємо значення одиниці, інакше – нуля. Розглядаючи|розглядуючи| всі можливі підмножини початкової|вихідної| множини|безлічі|, включаючи порожню|пусту| множину|безліч|, отримаємо наступний|такий| результат.

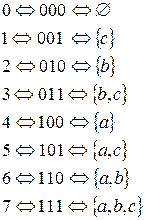
Як можна бачити, підмножини множини|безлічі| 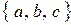відповідають восьми числам: 0, 1, ..., 7. Ми розглянули|розгледіли| всі бінарні комбінації в межах трьох біт. Як відомо, кількість таких комбінацій рівна .

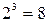Застосовуючи даний метод до множини|безлічі| з|із| чотирьох елементів, одержимо|отримаємо| кількість підмножин: 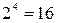. Для множини|безлічі| з|із| п'яти елементів: 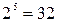. Узагальнюючи ці результати, приходимо до висновку, що множина|безліч| з|із| n елементів має підмножин.

Кантор був першим, хто став розглядати|розглядувати| потужності (кардинальні числа) нескінченних|безконечних| множин|безлічі|. Потужність рахункової множини|безлічі| він позначив староєврейською буквою|літерою| «алеф|» з|із| нульовим індексом: 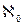. Потужність безлічі дійсних чисел, звану також потужністю континууму, позначив як: 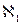. Відомо, що кардинальне число 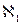більше кардинального числа 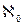. На початку 80-х років 19 століття|віку| Кантор висловив гіпотезу про те, що найближчою наступною|слідуючою| за 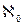потужністю є|з'являється,являється| потужність континууму 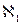. Узагальнена континуум-гіпотеза свідчить, що для будь-якої множини|безлічі| 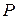перша потужність, що перевершує потужність цієї множини|безлічі|, є потужність безлічі всіх підмножин множини|безлічі| 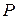. Таким чином , , …

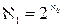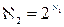Читайте також:

1. IV. Проблема антропогенних змін клімату або «парниковий ефект».
2. Актуальність і завдання курсу безпека життєдіяльності. 1.1. Проблема безпеки людини в сучасних умовах.
3. Альтернативність ресурсів і проблема економічного вибору
4. Близькосхідна проблема на рубежі 60-70-х років.
5. Вибір місця розташування підприємства як проблема прийняття рішень.
6. Виживання людини і людства–нагальна проблема сучасності
7. ВОДА В ЖИТТІ ЛЮДИНИ ТА ПРОБЛЕМА ЇЇ ОЧИЩЕННЯ.
8. Вступ. Здоров’я як проблема. Здоров’я - основне поняття
9. Географія і проблема взаємодії суспільства і природи.
10. Гуманізм епохи Відродження і проблема унікальної індивідуальності. Людина як творець самої себе
11. Демографічні процеси і проблема на українськиї землях к. 17- п. 19 ст. Багаттонаціональність як фактор соціальної історії
12. Діти з проблемами розвитку

Переглядів: 551