• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Типи об’єктів системи MAPLE та операції з ними

МІЖРЕГІОНАЛЬНА АКАДЕМІЯ УПРАВЛІННЯ ПЕРСОНАЛОМ

МУАП

Символьні обчислення в системі MAPLE

Частина 1

Київ 2005

Автори: А.В. Кузьмін, канд. фіз.-мат. наук, Н.М. Кузьміна канд. фіз.-мат. наук, І.К. Рисцов, канд. фіз.-мат. наук.

Рецензенти: кандидат фіз.-мат. наук, професор Рамський Ю.С.

Кандидат техн. наук Вишневський В.В.

Вступ

В останні роки показником інтелектуальних можливостей комп'ютерів стали новітні програмні системи символьної математики комп'ютерної алгебри [1-49]. Створені для проведення символьних перетворень математичних виразів, ці системи були доведені до рівня, що дозволяє значно полегшити, а часом і замінити, працю математиків, причому як теоретиків, так і математиків, що працюють в прикладній галузі. Вже з'явилися математичні відкриття, зроблені за допомогою таких програм. Навряд чи сьогодні є хоча б один серйозний науковий проект, зв'язаний з математичними дослідженнями де б не використовувались системи комп`ютерної математики.

Системи символьної математики довгий час були орієнтовані на великі комп'ютери. З появою персональних комп'ютерів та зростанням їх можливостей ці системи були адаптовані для персональних комп`ютерів і доведені до рівня масового комерційного продукту. Зараз на ринку систем символьної математики (чи комп'ютерної алгебри) пропонується різноманітний асортимент «продукції» — від розрахованої «на всіх» системи Mathcad [29-49], і до великих комп'ютерних програм, до яких можна віднести «велику трійку»: Mathematica [23-28], MATLAB [16-22] і Maple [1-15], що має тисячі вбудованих функцій і гарні можливості графічної візуалізації обчислень.

Усі ці системи працюють на персональних комп'ютерах, оснащених популярними операційними системами класу Windows. Але не тільки на них — є версії під операційні системи Linux, Unix, Mac і ін. Вони також знайомі користувачам великих комп'ютерів і навіть суперкомп'ютерів.

До середнього рівня таких систем відноситься система, що інтенсивно розвивається, Mathcad, яка має (на додаток до прекрасних засобів числових обчислень) придбане по ліцензії у фірми Waterloo Maple Inc. ядро символьних обчислень. Ядро системи Maple використовується й і в іншій системі — MATLAB, додаючи їй незвичайні для неї риси символьної математики.

Система Maple була створена групою вчених, керівництвом Кейта Геддеса (Keith Geddes) і Гастона Гонэ (Gaston Gonnet) у 1980 році в університеті Waterloo, Канада. Спочатку вона була реалізована на великих комп'ютерах і пройшла довгий шлях апробації, увібравши в себе велику частину математичних функцій і правил їхніх перетворень, вироблених математикою за сторіччя розвитку. Є реалізації цієї програми на платформах ПК Macintosh, Unix, Sun, а зовсім недавно спрощена версія Maple для операційної системи Windows СЕ стала використовуватися в мініатюрних комп'ютерах фірми Casio за назвою Cassiopeia.

Цій системі присвячені сотні книг. Відзначимо лише деякі з них [1-15], видані за рубежем. Досить повний список (близько 400 найменувань) книг по системах Maple можна знайти на сайте розроблювача цієї системи — компанії Waterloo Maple Software (www.maplesoft.com). Однак книг російською мовою особливо по останніх версіях цієї програми як і раніше мало.

Особливо ефективним є використання програми Maple при навчанні математики. Найвищий «інтелект» цієї системи сполучається з прекрасними засобами чисельного моделювання і відмінними можливостями графічної візуалізації. Застосування системи Maple, можливо як при викладанні, так і при самоосвіті, причому від самих основ і до вершин математики.

Практика показує, що найважливішим є перший етап освоєння системи. Перше знайомство з програмою багатьох користувачів просто зачаровує, переконавши користувача у безмежних можливостях можливостей системи і відсутності якого –не будь систематизованого опису. В результаті багато користувачів відкладають вивчення системи на потім.

Посібник що пропонується читачеві дозволяє йому швидко ознайомитись з великою кількістю функцій системи Maple, переглянути декілька десятків прикладів розв`язання задач за допомогою системи Maple та закріпити свої знання при виконанні великої кількості завдань для самостійного виконання., яких нараховується в посібнику біля 300. Велика увага в цьому посібнику приділено інтерфейсу користувача, і навчанню основним прийомам ефективної роботи із системою Maple в області математичних розрахунків, що відносяться до класу еквівалентних перетворень з математичними виразами, задач математичного аналізу (диференціальне та інтегральне числення функцій однієї та багатьох змінних), розв`язування рівнянь та систем рівнянь різного класу (алгебраїчних, лінійних систем, трансцендентних, рекурентних, диференціальних). У посібнику практично не розглядаються спеціалізовані пакети прикладних процедур, що призначаються для розв`язання вузькоспеціалізованих задач. Ця дуже потужна частина можливостей системи MAPLE буде розглядатися в наступних частинах посібника.

Maple — система комп'ютерної математики, розрахована на широке коло користувачів. Донедавна її називали системою комп'ютерної алгебри, що вказувало на особливу роль символьних обчислень і перетворень, що здатна здійснювати ця система. Але така назва звужує сферу застосування системи. Насправді, по-перше, вона здатна виконувати швидко й ефективно чисельні розрахунки, причому з необмеженою точністю, а по-друге, її можливості виходять далеко за рамки алгебри і вже покривають, наприклад, велику частину математичного аналізу.

Система Maple має широку сферу застосування від моделювання складних фізичних об'єктів, систем і пристроїв, і до створення художньої графіки (наприклад, фракталів). Заслуженою популярністю система Maple користаються у вузах — понад 300 самих великих університетів світу взяли її на озброєння. А число тільки зареєстрованих користувачів системи вже давно перевищило мільйон .

Maple — одна із самих могутніх інтегрованих систем символьної математики. Лідерство ця система завоювала в гострій конкурентній боротьбі з іншою математичною системою — Mathematica. Кожна з цих двох систем має свої особливості, але в цілому вони практично рівноцінні. Однак треба відзначити, що поява нових версій Maple від 7 до 9 означає черговий виток у змаганні цих систем за місце лідера світового ринку. Причому ривок цього разу зробила система Maple.

Maple — типова інтегрована система. Вона характеризується наступними властивостями:

має вбудоване ядро для перетворення математичних виразів;

потужну довідкову систему з великою кількістю прикладів;

чисельний і символьний процесори;

візуалізація обчислень, наукова та інженерна графіка;

бібліотека вбудованих функцій і додаткових пакетів;

вбудована мова програмування.

Тому Maple може застосовуватися як для проведення як класичних, так і прикладних математичних досліджень майже в усіх галузях науки, які використовують математичні моделі, включаючи економіку, фізику, екологією, біологію, соціологію . Іншими словами Maple це, ефективний , інструмент для математичного моделювання.

Перший розділ
Типи даних та перетворення над ними.

Типи об’єктів системи MAPLE та операції з ними

Система MAPLE може виконувати операції з об’єктами різної математичної природи зокрема

числами, константами, строками, змінними, невідомими величинами, виразами, функціями, списками, множинами, масивами.

Задавання чисел та виконання дій з ними.

У системі MAPLE можна задавати цілі числа. звичайні дроби, радікали, числа з плаваючою точкою, комплексні числа. Перші три типи чисел дозволяють виконувати над ними точні обчислення не використовуючи заокруглення.

Числа з плаваючою точкою є наближеними, у яких число значущих цифр є обмеженим і які використовуються для апроксимації точних чисел, зокрема дійсних.

Комплексні числа можуть бути як точними так і наближеними в залежності від того, точними або наближеними є дійсна і уявна частина цих чисел.

Цілі числа

Цілі числа задаються у вигляді послідовностей цифр від 0 до 9. Від’ємні числа задаються зі знаком (-) перед числом. Максимальне ціле число, яке можна задати у системі MAPLE обмежується величиною 2²⁸. Обчислення з цілими числами обмежуються арифметичними діями: додавання +, віднімання - , множення *, ділення /. та обчислення факторіалу!.

> 17-23;
> 24/6;
> 4*7;
> 15!;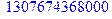

Окрім звичайних арифметичних операцій над цілими числами можна виконувати деякі команди:

розвинення цілих чисел на прості множники: ifactor():

обчислення частки двох чисел iquo(m,n);

обчислення залишку ділення двох чисел irem(m,n);

перевірка, чи є ціле число простим isprime(m)

> ifactor(34276);	.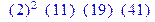
> iquo(49,8);
.> irem(49,8);
> isprime(34277);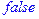
> isprime(347);

Звичайні дроби

Звичайні дроби задаються за допомогою операції ділення двох цілих чисел m/n. У випадку, коли дріб скорочується система MAPLE проводить це скорочення і записує результат. Якщо запис результату у вигляді звичайного дробу не дуже зручний, то його можна перетворити у десятковий дріб за допомогою оператора evalf(m/n,r),де параметр r задає кількість десяткових знаків мантиси. За замовченням ця кількість дорівнює 10 знакам.

> 65/7+2/3;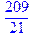
> evalf(%,3);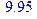

У останньому прикладі символ % у першому аргументі функції evalf вказує нарезультати попереднього обчислення.

Радикали

Радикали задаються як результат піднесення у дробову степінь цілих або дробових чисел, а також обчислення з них квадратного кореня.

> 1/4*3**(2/3)*4**(2/5);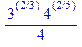

Система MAPLE прагне до виконання дій над радикалами точно, дивись наступний приклад:

> sqrt(3+2*sqrt(2))-sqrt(3-2*sqrt(2));

Дійсні числа с плаваючою точкою.

Дійсні числа з плаваючою точкою задаються у вигляді цілої і дробової частини, що розділені між собою десятковою точкою 24.3456 і перед яким може знаходитись знак + або -.

Часто числа з плаваючою точкою задаються у експоненціальному вигляді наприклад: 24.347 е-4 або 5.357 е 5. Частина числа, що знаходиться перед знаком е називається мантисою числа, яка множиться на 10 у степені значення якої розташоване за знаком е.

Комплексні числа

Комплексні числа задаються в системі MAPLE у вигляді суми дійсної та уявної яка містить спеціальну константу І, наприклад:

> (2/3+3*I); 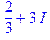Над комплексними числами можна виконувати арифметичні операції: +, -, *,/

> (2/3+2*I)+(1/3-I);
> (2/3+2*I)-(1/3-I);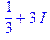
> (2/3+2*I)*(1/3+I);
> (2/3+2*I)/(1/3-I);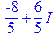

Для отримання з комплексного числа його дійсної та уявної частини можна використовувати функції Re() та Im(). Комплексно спряжене число можна отримати за допомогою функції conjugate(). Модуль і аргумент комплексного числа можна отримати за допомогою функцій abs(), та argument()

> conjugate(-8/5+6/5*I);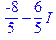
> abs(-8/5+6/5*I);
> argument(-8/5+6/5*I);
> Re(-8/5+6/5*I);Im(9-8/5+6/5*I);	;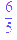

Для обчислення над комплексними числами використовується функція evalc()

> evalc(argument(((1/2)^(1/2)- I*(1/2)^(1/2))^(1/4)))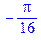

Задавання констант

Система MAPLE використовує набір загально прийнятих констант, таких як:

false “істина”;

true “хиба”;

gamma константа Ейлера;

Pi число p;

I уявна одиниця ;

infinity нескінченість .

Константи Pi та gamma можна обчислювати з певною точністю використовуючи функціюevalf()

> evalf(Pi,7); > evalf(gamma,12);

Задавання стрічок

Система MAPLE дозволяє працювати зі стрічками – довільним набором символів, який записується у подвійні лапках. Кожний символ в стрічці представляє самого себе. Довжина стрічки практично не обмежена і може досягати майже 268 млн. символів. За допомогою функції length() можна обчислити довжину стрічки. MAPLE трактує стрічку як масив символів, тому є можливість звернутися як до окремого символу масиву, так і до частини стрічки.

> S:="FRAZA";

> length(S);

> S[3];

> "FRAZA"[2..4];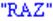

Для об'єднання двох стрічок в єдину використовується операція конкотенації || або функція cat().

> "FRAZA"||"235";

> cat( "FRAZA","235");

Змінні, невідомі, вирази та функції в MAPLE

Змінні в системі MAPLE мають своє ім’я, яке починається з літери. Великі і малі літери в імені змінної відрізняються між собою. Імена змінних не повинні містити пробілів, які можна заміняти знаком підкреслювання. Для іменування змінних не можна використовувати зарезервовані слова MAPLE та назви констант. При використанні цих слів для іменування змінних система MAPLE повідомляє про помилку. Для того щоб дізнатися про список зарезервованих слів можна звернутися до довідки системи MAPLE за допомогою оператора ,? protect.

Вирази у MAPLE представляють собою комбінацію імен змінних, чисел, функцій, що з’єднуються між собою знаками допустимих арифметичних операцій.

Якщо вираз використовує змінну, якій не присвоєно ні якого числового значення, то така змінна вважається невідомою величиною, а такий вираз називається символьним виразом. Саме для таких виразів і розроблялася система MAPLE.

Важливою операцією в MAPLE є операція присвоювання, яка має наступний синтаксис

змінна: = вираз .

За замовченням кожна змінна MAPLE має тип symbol, представляє символьну змінну, а її значення м є її ім’я. При записі виразів система MAPLE дозволяє використовувати дуже багатий набір функцій. Елементарних: експоненціальна, логарифмічна, квадратний корінь, модуль, знак числа, факторіал, тригонометричні функції, гіперболічні функції, обернені тригонометричні функції. Та спеціальних функцій: функцій Бесселя, еліптичних інтегралів, Дірака, гамма та інші. Для знаходження необхідної функції користувач може використати довідникову систему MAPLE за допомогою команди ?inifunction;

Для задавання функції користувача та її багаторазового використання можна використовувати функціональний оператор у вигляді vars->result.

> ff:=x->(sin(x)+cos(x))/x^2;
> evalf(ff(2));
> ff1:=(x,y)->sin(x)*sin(y)/(sin(x)+sin(y));
> evalf(ff(2,3));

 

Для створення функцій, що приймають різні аналітичні вирази у різних областях зміни незалежної змінної, так званих кускових функцій у системі MAPLE використовується спеціальний оператор

piecewise(cont_1, f_1, cont_2, f_2, ….cont_n, f_n, ), де cont_1,cont_2,…cont_n – логічні вирази, f_1,f_2,…f_n,f_other – вирази, що задають функціональні залежності.

 

> piecewise(-infinity <x and x<=0,x^2, 0<x,x);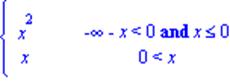
> piecewise(x^2+y^2<=1, x^2+y^2, 1/sqrt(x^2+y^2));

Складні типи виразів системи MAPLE.

Крім перелічених вище простих типів даних, система MAPLE ефективно працює з складними типами даних до яких відносяться :

Послідовності виразів;

Списки виразів;

Множини виразів;

Масиви;

Матриці.

Складні типи даних утворюються з простих типів даних за допомогою спеціальних синтаксичних конструкцій.

Послідовності виразів

Послідовність виразів є самостійним базовим об'єктом MAPLE за допомогою якого будуються інші складні об’єкти. Послідовність виразів , або просто послідовність, - це група виразів, що розділена комами. Базовою властивістю послідовності є збереження порядку слідування виразів. Послідовність може містити вирази, що повторюються, які розташовані у довільному порядку. На послідовність можна дивитися як на послідовність виразів, перенумерованих натуральними числами починаючи з одиниці.

Для послідовності її тип має ім’я exprseq. Для задавання послідовності використовується оператор присвоювання у правій частині якого використовується послідовність виразів, або в лівій частині використовується послідовність змінних.

Для послідовностей є можливість звертатися як до послідовності в цілому, так і до окремих її елементів, вказуючи у квадратних дужках поруч з іменем змінної номер елемента послідовності, або діапазон номерів послідовності, що вказується у квадратних дужках у вигляді [n..m].

В той же час присвоїти нове значення елементу послідовності використовуючи індексну форма елемента послідовності у лівій частині оператора не можна.

Для задавання довгих послідовностей використовується оператор seq зтаким синтаксисом:

seq(f, i= n..m);

seq(f, i= s);

деf -вираз, що залежить від змінної i ;

i -змінна, що визначає порядковий номер елемента послідовності;

n,m –числа, що задають діапазон зміни величини і з кроком 1 ;

s –може бути списком, множиною, послідовністю, стрічкою

 

> s1:=1,x,x^2,x^3;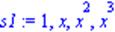
> whattype(s1);
> s1[2..4];
> s1[2]:=y;	invalid assignment (1, x, x^2, x^3)[2]:= y; cannot assign to an expression sequence
> a,b,c,d:=s1;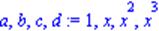
> a;b;c;d;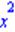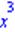
> s2:=seq(1/(j^(3/2)), j=1..10);	s2 := 1, 1/4*2^(1/2), 1/9*3^(1/2), 1/16*4^(1/2), 1/25*5^(1/2), 1/36*6^(1/2), 1/49*7^(1/2), 1/64*8^(1/2), 1/81*9^(1/2), 1/100*10^(1/2)
> s3:=seq(1/i,i=s1);

Списки та множини

Список будемо називати впорядковану послідовність виразів, що записується у квадратні дужки. Множиною будемо називати не впорядковану послідовність елементів, записану у фігурних дужках. Якщо в послідовності присутні елементи, що повторюються, то кожний з них є окремим елементом списку, і одним і тим же елементом у множині. Порядок елементів у списку е важливим і список зберігає порядок слідування елементів. За допомогою індексної форми списку можна звернутися до будь – якого елемента списку, та присвоїти йому нове значення. При задаванні множини елементів порядок елементів є неважливим і може змінюватися системою MAPLE самостійно. Індексну форму можна використовувати і для елемента множини для вибору відповідного елемента множини, але за допомогою індексної форми не можна присвоїти елементу множини нове значення.

Для вибору декількох елементів списку або множини за допомогою індексної форми можна використовувати діапазон, при цьому додатне значення індексу відповідає відліку елементів списку, або множини зліва направо, а від’ємне значення індексу з права наліво. Для задавання усіх елементів списку S можна записати індексний вираз S[1..-1], тобто індекс – 1 відповідає останньому елементу списку, а індекс –2 передостанньому елементу списку або множини.

> sp1:=[1,x,x^2,x^3,x^4];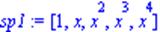
> sp1[2];
> sp1[3..-1];
> sp1[3]:=y^2;
> sp1:=sp1;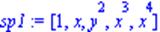
> Mn1:={a,b,c,a,b,c,d,f,a};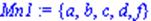
> Mn1[2..4];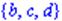
> Mn1[4];
> Mn1[4]:=dd;	cannot reassign the entries in a set

Над множинами можна виконувати теоретико – множинні операції, а саме операції об`єднання множин union, різниці множин minus, перетину множин intersect.

> Mn2:=Mn1 union {e,g};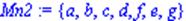
> Mn3:= Mn2 minus {b};
> Mn4:=Mn2 intersect Mn3;

Масиви

Для створення масиву у системі MAPLE необхідно використати оператор array(границі, список).Де параметр границі задає діапазон, або діапазони зміни індексу (індексів) масиву. Для багатовимірних масивів відповідні діапазони повинні задаватися підряд через кому. Параметр список призначений для задавання елементів масиву у вигляді вкладених списків з глибиною вкладання , що дорівнює розмірності масиву. Перший і другий параметри функції arrayє необов’язковими однак або перший або другий повинен бути заданий. Якщо значення елементу масиву не задані функцією array,то ці значення можна присвоїти використовуючи індексну форму елементів масиву в лівій частині оператора присвоювання. При введенні імені масиву MAPLE лише повторює його ім’я, але не зображає його елементи. Для отримання елементів масиву необхідно використати оператор print(ім’я_масиву), який приведе до зображення на лістингу MAPLE елементів масиву. Для двовимірних масивів з індексами , що починаються з одиниці зображення цих масивів здійснюється у вигляді матриць.

 

> MM:=array(1..4,1..4,[[1,2,3,4], [2,3,4,5],[3,4,5,6],[4,5,6,7]]);
> MM1:=array(1..4,1..4,[seq([seq( i+j,i=1..4)],j=1..4)]);
> MM[2,1];MM;
> MM[3,3]:=100;
> print(MM);
MM2:=array(1..2,1..2,1..2,[[[a,b],[c,d]],[[a1,b1],[c1,d1]]]);	MM2 := ARRAY([1 .. 2, 1 .. 2, 1 .. 2], [(1, 1, 1) = a, (1, 1, 2) = b, (1, 2, 1) = c, (1, 2, 2) = d, (2, 1, 1) = a1, (2, 1, 2) = b1, (2, 2, 1) = c1, (2, 2, 2) = d1])

 

> SM:=[seq([seq(m[i,j],j=1..3)], i=1..3)];

 

 

>SM:=[seq([seq(m[i,j],j=1..3)],i=1..3)]: > MMM:=array(SM);

---

Читайте також:

1. I. Органи і системи, що забезпечують функцію виділення
2. I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
3. II. Анатомічний склад лімфатичної системи
4. IV. Розподіл нервової системи
5. IV. Система зв’язків всередині центральної нервової системи
6. IV. Філогенез кровоносної системи
7. Pancakes with Maple Syrup
8. POS-системи
9. T. Сутність, етіологія та патогенез порушень опорно-рухової системи
10. VI. Філогенез нервової системи
11. А) Заробітна плата її форми та системи.
12. А) Заробітна плата, її форми та системи.

---

Переглядів: 2994

<== попередня сторінка	|	наступна сторінка ==>
Знайти координати центра мас однорідної фігури Ф, обмеженої вказаними лініями	|	Команди перетворення виразів

Не знайшли потрібну інформацію? Скористайтесь пошуком google: