
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Команда спрощення виразів simplify()
Ця команда призначена для здійснення операції спрощення виразів, які включають в себе раціональні функції, тригонометричні функції, логарифмічні та експоненціальні функції.
Команда має декілька форм використання : simplify (вираз); У дужках задається вираз, який повинен бути спрощений. Для спрощення окремих типів виразів раціонально використовувати додаткові параметри команди simplify (вираз, n1,n2,…). Тут n1,n2,… є імена процедур спрощення виразів, а саме:
exp- для спрощення функцій з експоненціальними виразами;
ln - для спрощення виразів з логарифмами;
sqrt - для спрощення виразів з квадратними коренями;
trig- для спрощення тригонометричних виразів;
radical- для спрощення виразів з дробовими степенями;
power - для спрощення виразів з степенями, експонентами, логарифмами.
Крім того в якості параметра процедури simplify можна використовувати параметр виду assume = властивість. Де парметр властивість може приймати одне з наступних значень:
complex - комплексна область;
real - дійсна область;
positive - додатні дійсні числа;
integer - цілі числа;
RealRange(a,b) - інтервал (a,b) дійсних чисел.
Команда спрощення дозволяє задавати правила спрощення користувача, які користувач пропонує використати при виконанні спрощення відповідного виразу.
Ці правила задаються у команді simplify()другим параметром і мають наступний вигляд { рівність 1, рівність 2,…}.
Розглянемо приклади використання оператору спрощення виразів:
| > simplify(((x-a)^2+x*(x-a)+x^2)/((x-a)^2-x*(x-a)+x^2)-19/7); | 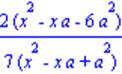
| |
| > R1:=((x-a)*sqrt(x-a)+(x-b)*sqrt(x-b))/(sqrt(x-a)+sqrt(x-b))+a+b; | 
| |
| > simplify(R1,sqrt,symbolic); | 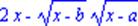
| |
| >R2:=log[a](sqrt(a^2-1))* (log[1/a](sqrt(a^2-1)))^2/ (log[a^2](a^2-1)*log[a^(1/3)]((a^2-1)^(1/6))): > simplify(R2); | 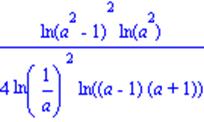
| |
| >simplify(%,{ln(1/a)=-ln(a), ln(a^2)=2*ln(a)}); | 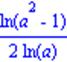
| |
| > r4:= (1-2*(cos(v))^2)/ (sin(v)* cos(v))+ 2*tan(2*v)+ cot(4*v)-3; | 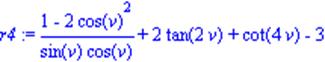
| |
| >simplify(r4,trig); | 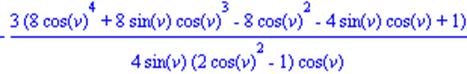
|
Команди розкриття дужок у виразах expand()
Команда expand()виконує розкриття дужок і перетворює добутки у суми у будь – яких алгебраїчних виразах. Ця команда виконується для будь – яких поліномів та для частки двох поліномів. У випадку частки двох поліномів ця команда розкриває дужки у чисельнику і ділить кожний член отриманого виразу на знаменник, який вона не змінює. Крім того команда expand()вміє розкривати дужки для більшості математичних функцій: sin(x), cos(x), tg(x), ln(x),exp(x), sh(x), ch(x) та інших.
> expand(sin(x+y)*sin(y+z));


> expand((a*x^2+b*x^3)*(b*x^3+3*a*x*2));

Команда приведення декількох членів виразу до одного, команда combine
Команда combine() приводить декілька членів, представлених сумою, добутком, або степенями до одного члена, використовуючи різноманітні правила, які є фактично оберненими правилам перетворення команди expand().
| >d1:=sin(x)*cos(y)+cos(x)*sin(y); > combine(d1); | 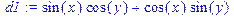

|
| > assume(x>0);assume(y>0); > d2:=2*ln(x)+3*ln(y); > combine(d2); > d1:=exp(2*x)*exp(y)/exp(z); > combine(d1); | 
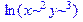


|
Розвинення полінома на прості множники, функція factor()
Призначення функції factor() провести розвинення на множники поліному від декількох змінних.
Під поліномом у системі MAPLE розуміють вирази, що містять невідомі величини, у яких кожний член має вигляд добутку цілих невід’ємних степенів невідомих величин з числовими або алгебраїчними коефіцієнтами. Невідома величина у поліномі може бути представлена викликом деякої функції, аргумент якої є невідома величина. Команди розвинення поліному має вигляд factor( exp,K) де exp – вираз, що підлягає розвиненню на множники, а K – необов’язковий параметр, який уточнює над яким полем числових коефіцієнтів здійснюється розвинення на множники. Цей параметр може приймати значення real complex, мати значення одного радикалу, або списку радикалів.
| > factor(x^3+3,3^(1/3)); | 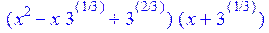
|
| >factor(x^3+3,real); | 
|
| > factor(x^3+3,complex); | 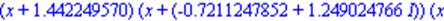 
|
| > factor(x^3-y^3); | 
|
| >factor(x^3-y^3,(-3)^ (1/2)); | 
|
| >factor(x^3-3,complex); | |
| >x^2+x*3^(1/3)+3^(2/3); | 
|
| > evalf(%); | 
|
> factor(%,complex);
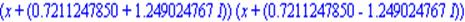
|
Скорочення алгебраїчного дробу команда normal().
Призначення команди normal() полягає у приведенні виразів, що містять алгебраїчні дроби до спільного знаменника і спрощення отриманого алгебраїчного дробу шляхом скорочення чисельника і знаменника. Команд normal() має наступний вигляд normal(f, expanded). Де f – алгебраїчний дріб, а необов’язковий параметр expanded вказує на те, що після скорочення дробу у чисельнику і знаменнику розкриваються дужки.
> gg1:= 1/(x+1)^2 +3/(x-1)^2+ 4/((x-1)*(x+1));
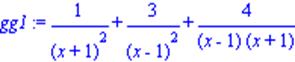
> normal(gg1); > normal(gg1,expanded);


Команда приведення подібних членів collect()
Команда collect()працює з узагальненими поліномами декількох змінних – поліномами, в яких в якості невідомих можуть виступати функції з аргументами, що є невідомими величинами в MAPLE. Синтаксис цієї команди має три форми:
collect(exp,x) ; collect(exp,x,form,func) ; collect(exp,x,func)
exp -вираз, у якому необхідно провести комплектування виразу по степеням невідомих;
x -ім’я невідомої величини, список, множина невідомих величин у випадку поліному декількох змінних, або ім’я функції з аргументом – невідомим.
form -має два значення recursive або distributed має зміст для многочленів декількох змінних і впливає на алгоритм приведення подібних членів відносно обраного списку змінних.
func -параметр що визначає ім’я команди, яка використовується по відношенню до отриманих коефіцієнтів, зазвичай simplify()абоfactor().
| > s:= 2*x^3*a^2*y^2+ 3*x^3*y^2*b+2*x^2*y^3*a^2+4*a*x^2*y^3; | 
|
| > collect(s,[y,x]); | 
|
| > collect(s,[x,y], factor); | 
|
| >s1:=2*a*(sin(x))^2+3*b^2*(sin(x))^2*x^2+15*x^2*sin(x)+2*c*sin(x); | 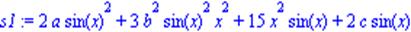
|
| > collect(s1,sin(x)); | 
|
Структура виразів та робота з ними
Дуже часто для виконання певних дій з виразами з’являється необхідність виділити з виразу його частину та провести з нею певні перетворення , або замінити її на деякий інший вираз. В таких випадках треба знати структуру виразу і вміти з нею працювати шляхом звернення до будь - якої частини. Будь – який вираз у системі MAPLE представляється у вигляді ієрархічної структури в якій кожний об’єкт розділяється на підоб’єкти першого рівня, які у свою чергу діляться на підоб’єкти другого рівня і так далі. Процес виділення підоб’єктів продовжується до тих пір , поки не будуть виділені базові прості елементи MAPLE, такі як цілі числа, дійсні числа, дроби, змінні величини символьного типу, функції списки, послідовності, множини, масиви та інші.
Для роботи з виразами корисним будуть функції:
lhs(egn)виділяє ліву частину рівності egn;
rhs(egn)виділяє праву частину рівності egn;
numer(exp)виділяє чисельник дробу exp;
denom(exp)виділяє знаменник дробу exp.
| >eq1:=(a*x^2+b*x+c)/tan(x)=x*sin(x); | 
|
| > rhs(eq1); > lhs(eq1); | 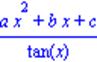

|
| > numer(rhs(eq1)); > denom(rhs(eq1)); | 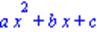

|
Для більш детального вивчення структури виразу використовуються наступні функції MAPLE.
whattype(exp) повертає тип виразу exp
op(exp) повертає список об’єктів першого рівня виразу exp
op(k..n,exp) (op(k,exp)) повертає список від к –го до n –го об’єкту (k –й об’єкт) першого рівня виразу exp, при к = 0 повертається тип виразу exp.
nops(exp) повертає число об’єктів першого рівня в виразі exp.
| > op(0..nops(eq1),eq1); | 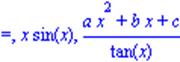
|
| > eq11:=op(1,eq1); > eq12:=op(2,eq1); | 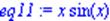
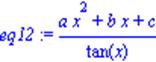
|
| > op(0..nops(eq11),eq11); > op(0..nops(eq12),eq12); | 

|
| > eq121:=op(1,eq12); | 
|
| > op(0..nops(eq121),eq121); | 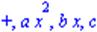
|
| > op(1,eq121); | 
|
| > op(2,eq12); | 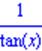
|
| > op(op(2,eq12)); | 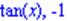
|
| > op(1,op(2,eq12)); | 
|
Обчислення виразів
У програмі символьних обчислень MAPLE користувач зустрічається з поняттям обчислення символьних імен. Подібна функція відсутня для систем численних обчислень. Здебільшого система MAPLE використовує алгоритм повного обчислення символьної змінної. Тобто, у випадку, коли необхідно обчислити значення символьної змінної перевіряється, чи присвоювались цій змінній які - небудь значення, якщо да , то воно підставляється замість імені змінної і перевіряється, чи містять підставлені значення невідомі змінні. Якщо містять, то перевіряється, чи були присвоювання цим змінним певних значень, якщо були то вони підставляються замість значень змінних. Цей процес продовжується рекурсивно поки замість усіх імен не будуть підставлені присвоєні їм значення, або якщо деяким змінним нічого не присвоювалось, то такі змінні залишаться в виразі як невідомі величини.
Для повного обчислення значення будь – якої змінної можна просто вказати її ім’я і в результаті система MAPLE виконає повне обчислення значення цієї змінної, або можна використати команда eval(x) де x ім’я відповідної змінної, яку необхідно обчислити.
Правило повного обчислення значення змінних при задаванні імені змінної діє для змінних усіх типів за винятком змінних, які містять масиви, матриці таблиці та процедури. Для цих змінних діє правило обчислення до значення останнього присвоєного символьного імені. Для виконання повного обчислення такої змінної необхідно явно ініціювати команду eval(Y).
У випадку, коли необхідно просто обчислити ім’я змінної не використовуючи алгоритм повного обчислення значення цієї змінної можна використати оператор evaln(x); або той же самий результат зможемо отримати за допомогою запису імені відповідної змінної у одинарних кавичках ‘x’. Вказаний оператор можна використовувати для того, щоб анулювати усі попередні присвоювання здійснені по відношенню до цієї змінної, що дозволить використовувати її просто як невідому величини з значенням, що дорівнює імені змінної.
| > x:=a*c; c:=b^2+2; a:=(d+e)^3; |  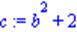 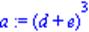
|
| > x; > eval(x); | 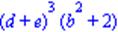 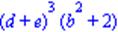
|
| > y:=d+e; | 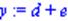
|
| > x*y; > eval(x*y); | 

|
| > x/y; | 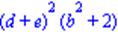
|
| > evaln(x); > evaln(y); | 

|
| > x:=evaln(x); | 
|
| > x; | 
|
| > y:='y'; > y; | 

|
На практиці в математичних дослідженнях дуже часто виникає задача обчислення значення математичного виразу або функції при конкретному значені змінних величин, що входять до відповідного виразу. Для того, щоб зберегти сам вираз і в той же час обчислити його значення при вказаних значення параметрів можна скористатися оператором eval(expr, [eq1,eq2,…eqn]); Де expr – математичний вираз, що містить змінні величини, Параметри eq1,eq2,…eqn – рівності, що задають значення змінним величинам, при яких повинен бути обчисленим відповідний вираз expr.
| > g:=2*x^3*y+3*x*y^3+5*x*y; | 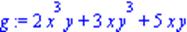
|
| > gg:=eval(g,x=1); | 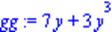
|
| > gg1:=eval(gg,y=1); | 
|
| > eval(g,[x=1,y=1]); | 
|
Система MAPLE прагне провести обчислення будь – якої величини точно і використовує арифметику дробових чисел та радикалів там де це можливо. Якщо при проведені обчислень результат можна отримати лише у вигляді ірраціонального числа, або більш доцільно отримувати числа у вигляді звичайних десяткових дробів з заданою кількістю знаків після коми, то для обчислення значення виразу можна використовувати оператор evalf(f,n),де f вираз що необхідно обчислити , а n – число значущих цифр, які використовуються при обчисленнях(за замовченням n=10).
Зверніть увагу на різницю між значеннями однакових виразів, що обчислені за допомогою операторів evalта evalf
| > f:=x->sin(x)/x; | 
|
| > eval(f(Pi/4)); | 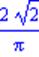
|
| > evalf(f(Pi/4),20); | 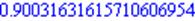
|
| > evalf(1/3*x^2+sin(Pi/4)*x+sqrt(3),6); | 
|
| > eval(1/3*x^2+ sin(Pi/4)*x+sqrt(3)); | 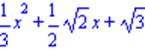
|
Система MAPLE використовує ще цілий ряд функцій призначених для проведення обчислень виразі:
evalc для обчислення виразів, що приймають комплексні значення;
evalb для обчислення виразів, що приймають булєві значення;
evalm для обчислення матричних виразів;
evalr для обчислення інтервальних виразів.
З цими функціями можна ознайомитись за допомогою довідникової служби системи MAPLE.
Перетворення виразів за допомогою підстановок
Для аналітичного перетворення виразів і зокрема для їх спрощення в математиці використовуються операція підстановок де замість одних змінних та виразів здійснюється підстановка інших змінних та виразів. В системі MAPLE існують декілька команд, які виконують відповідні функції. До цих команд відносяться:
subs(x = a, exp)–у виразі exp заміняє x на a.
subs(s1,s2…sn, exp)-у виразі exp заміняє одні підвирази на інші обираючи їх зі списку s1,s2…sn, кожний елемент списку має вигляд x=a. Підстановки виконуються послідовно.
subsop(N1=a1,…,Nk =ak, exp) –у виразі exp заміняє підвираз з номером N1 на підвираз a1…з номером Nk на підвираз ak, де номер підвиразу визначається за допомогою аналізу структури оператором op(n, exp).Усі підстановки виконуються послідовно.
algsubs(x=a,exp) -у виразі exp заміняє підвираз x на підвираз a.
Між командами subs іalgsubsнезважаючи на їх схожість є суттєва різниця, яка полягає у наступному. Процедура subsздійснює заміну підвиразу x на підвираз a лише у випадку, коли підвираз х входить, як синтаксичний елемент структури виразу exp. Процедура algsubsздійснює заміну підвиразу x на підвираз a, у випадку, коли підвираз x входить як алгебраїчний підвираз виразу exp.
| >2*x^3+3*x^2*z+sqrt(x); | 
|
| >algsubs(x^2=y,2*x^3*y+3*x^2*z+sqrt(x)); | 
|
| >subs(x^2=y,2*x^3+3*x^2*z+sqrt(x)); | 
|
| >subs(u/v=z,3*u^3/(2*v^2)+u/v); | 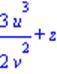
|
| >algsubs(u/v=z,3*u^3/(2*v)+u/v); | 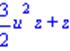
|
| >subsop(2=z,3*u^3/(2*v)+u/v); | 
|
| >subsop(1=x,2=z,3*u^3/(2*v)+u/v); | 
|
| >eqq1:=2*(sin(x))^(1/2)*cos(x)+cos(x)/sin(x); | 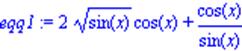
|
| >subs(sin(x)=sqrt(1-(cos(x))^2), eqq1); | 
|
| >algsubs(sin(x)=sqrt(1-(cos(x))^2), eqq1); | 
|
| >algsubs(1/sin(x)=1/sqrt(1-(cos(x))^2) , eqq1); | 
|
| >subs(x^2=y,z=x^2,sqrt(x)=r,2*x^3+3*x^2*z+sqrt(x)); | 
|
Обмеження на невідомі
Для проведення різноманітних математичних обчислень і перетворень дуже часто необхідно накладати на відповідні змінні певні обмеження, робити відносно невідомих певні припущення. У системі MAPLE існує декілька команд, які дозволяють вводити і перевіряти обмеження, накладені на змінні або цілі вирази.
Команда assume(x,властивість) накладає на змінну х відповідну властивість. Тут х представляє собою змінну, або вираз який включає таку змінну. Властивістьможе приймати такі найбільш широковживані значення
| Властивість | Опис властивості |
| negative | від’ємні дійсні числа |
| nonnegative | Невід’ємні дійсні числа |
| positive | Додатні дійсні числа |
| natural | Натуральні числа (0,1,2,3…) |
| posint | Цілі, строго більше 0 |
| odd | Непарні числа |
| even | Парні числа |
| complex | Комплексні числа |
| real | Дійсні числа |
| rational | Раціональні числа |
| integer | Цілі числа |
Пару параметрів (x,властивість)можна замінити математичним відношенням, наприклад: assume(x>0); assume (x>=0).Якщо на змінну накладені обмеження , то у результатах перетворень з цією змінною ця змінна виводиться за замовченням зі знаком (~).
Команда assume може отримувати декілька пар (x,властивість)або математичних відношень, наприклад assume(x>1, x<=2).
Нове обмеження, що накладається новою командою assume()на змінну відміняє усі попередні обмеження
Для послідовного додавання додаткових обмеженьпо ходу розв’язування задач можна використовувати команду additionally ()з параметрами аналогічними параметрам команди assume, наприклад assume (x>=0), additionally(x<=100). Таким чином обмеження накладені двома останніми операторами накладають на змінну х обмеження 0 <=x<=100.
За допомогою функції is(), яка вертає значення true або false в залежності від того задовольняє змінна відповідній властивості або ні.
| >assume(x>5, y<-10); > is(x*y < 50); | 
|
| >assume(x>y,y>0); is(x<0); | 
|
| >assume((2*i+2)/2,integer); is(i,integer); | 
|
Перетворення виразів в тотожні форми, команда convert()
Більшість математичних виразів мають різноманітні математичні форми запису. Здебільшого перетворення виразу з однієї форми в іншу дозволяє отримати вираз більш зручний для подальшого використання. Крім того різні функції Maple працюють з різними формами виразів і різними типами даних. Тому велике значення має цілеспрямоване перетворення виразів та даних.
Основною функцією для таких перетворень є функція convert:
convert(expr, form, аrgЗ. ...)
Тут ехрr — довільний вираз, form — найменування форми, аrg3, ... — необов’язкові додаткові аргументи.
convert — досить проста і разом з тим потужна функція.. ЇЇ потужність полягає у можливості множину параметрів. Їх повний перелік нараховує (76 штук!) можна знайти в довідці по функції convert.
| > convert( [2,3,4,26], `+`); | 
|
| > ff := seq( (f[i]^i)/i, i=1..6 ); > convert([ff], `*`); | 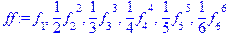

|
| >d1:=convert(x^4/(x^5+1),parfrac,x); | 
|
| >convert(op(1,d1),parfrac,x,real); | 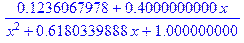 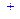

|
| > f := sin(2*x)*cos(x); | 
|
| > convert(f, tan,x); | 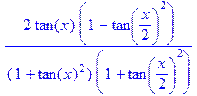
|
| > d:=tan(x)/(1-(tan(x))^3); > d:=convert(d,sincos,x); > normal(d); | 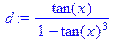
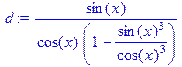
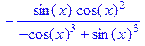

|
Завдання для самостійного виконання до першого розділу
1. Для заданих цілих чисел m, n і k:
· Визначити, які з них є простими;
· Непрості цілі числа розкласти на прості множники;
· Знайти цілу частину від операції ділення m на k;
· Знайти залишок від операції ділення m на k;
· Для одного з непростих чисел знайти суму його простих множників;
· Утворити дроби m/n n/k та знайти суму та різницю цих дробів.
1.1 m =3647, n = 24567, k =347 ;
1.2 m= 459, n= 4591, k = 34567;
1.3 m= 4153, n= 45683, k= 23798; .
1.4 m= 574 , n= 35671, k= 76452 .
1.5 m= 341, n= 4573, k=56737 .
2. Для заданих комплексних чисел z1 і z2 :
· Знайти їх суму та різницю;
· Знайти їх добуток та частку;
· Знайти модуль та аргумент числа z1;
· Записати комплексно спряжене число до z2
· Знайти модуль та аргумент комплексних чисел z1 і z2

2.1 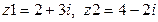
2.2 
2.3 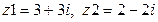
2.4 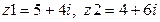
2.5 
3. Задайте три стрічкові константи: Ваше прізвище, ім’я, по батькові, записаних латинськими літерами
Визначте кількість символів у кожній стрічковій константі.
Створіть стрічкову константу яка представляє собою стрічку, що містить Ваше ім’я, по батькові та прізвище.
Створіть з попередньої стрічки нову стрічку, яка об’єднує літери попередньої стрічки починаючи з третьої по шосту та три передостанні літери.
Створіть стрічкову константу яка містить Ваші ініціали ПІБ.
4. Задати функцію.
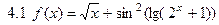




5. Задати функцію
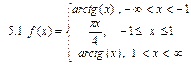


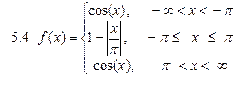

6. Утворити послідовність елементів (виразів):

6.1 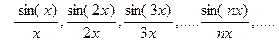 6.2
6.2 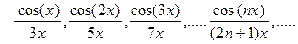
6.3 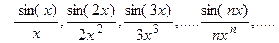 6.4
6.4 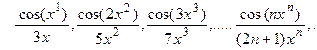
6.5 
7. На базі послідовностей пункту 6 утворити список з 12 елементі починаючи з номера, що відповідає номеру Вашого варіанту. Обчислити суму другого, сьомого та дев’ятого елементів списку. Знайти відношення п’ятого та дев’ятого елементів списку. Останнє значення добавити у кінець списку.
8. Утворити множини елементів. Побудувати множини, які є об’єднанням, перетином та різницею першої та другої множини.

8.1 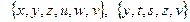 8.2
8.2 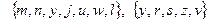
8.3 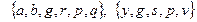 8.4
8.4 
8.5 
9. Задати матрицю 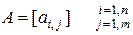 розмірністю m*n:
розмірністю m*n:

9.1 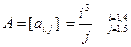 9.2
9.2 
9.3 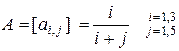 9.4
9.4 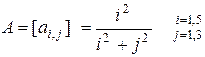
9.5 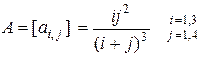
10. Задати символьну матрицю M=[m i,j] i=1,n j=1,m розмірність, якої співпадає з розмірністю матриці в попередньому завданні. Присвоїти елементу другого стовпця та третьої стрічки цієї матриці значення цього елементу з попереднього завдання 
11. Використовуючи операції перетворення виразів довести наступні алгебраїчні тотожності.
11.1  ;
;
 11.2
11.2 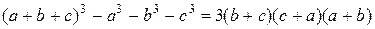 ;
;
 11.3
11.3 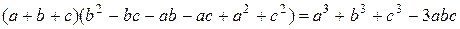 ;
;

 11.4
11.4 
 11.5
11.5 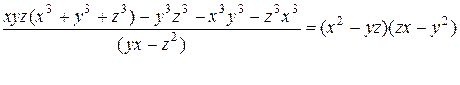
12. Спростити наступні вирази:
12.1 
 12.2
12.2  12.3
12.3 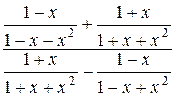
12.4  12.5
12.5 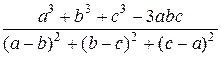
13. Довести умовні тотожності:
13.1 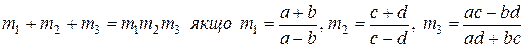
13.2 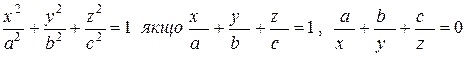
13.3 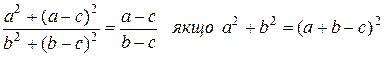
13.4 
13.5 
14. За допомогою аналізу структури виразів присвоїти змінній struct значення виділеного у фігурних дужках виразу.
14.1 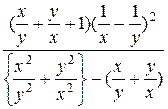 14.2
14.2 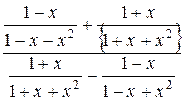
14.3 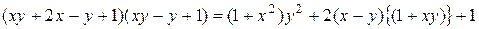
14.4 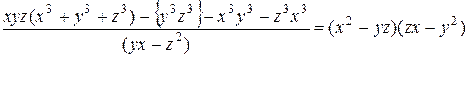
14.5 
15. Враховуючи область визначення функцій провести спрощення наступних виразів:
15.1 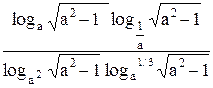
15.2 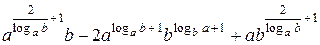
15.3 
15.4 
15.5 
16. Довести тригонометричні тотожності.
16.1 
16.2 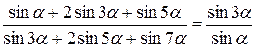
16.3 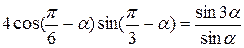
16.4 
16.5 
Другий розділ
Розв`язування задач математичного аналізу за допомогою системи MAPLE
Система аналітичних обчислень MAPLE має багатий набір вбудованих функцій призначених для розв`язування класичних задач математичного аналізу а саме:
обчислення границь послідовностей;
обчислення границь функцій однієї змінної та декількох змінних;
обчислення похідних та диференціалів функцій однієї змінної та багатьох змінних;
розвинення функцій за формулою Тейлора та за формулою Лорана, знаходження розкладів у узагальнені степеневі ряди;
знаходження невизначених інтегралів;
обчислення визначених інтегралів;
обчислення сум та добутків;
обчислення сумі рядів;
виконання заміни змінних в диференціальних та інтегральних виразах;
обчислення багатовимірних інтегралів;
обчислення криволінійних інтегралів;
обчислення поверхневих інтегралів та інші
Обчислення границь послідовностей та функцій
Для обчислення границь функцій використовується стандартна функція limit або Limit, друга функція представляє собою пасивну форму функції. загальна форма функції limit або Limitмає вигляд: , limit (f(x),x=a,dir), Limit(f(x),x=a), Limit (f(x),x=a,dir), де f(x) – алгебраїчний вираз, що залежить від x, x – ім`я змінної, a – точка в якій обчислюється значення границі, dir – параметр, який вказує на напрямок пошуку границі він приймає значення (left – пошук односторонньої границі зліва, right – пошук односторонньої границі справа, real – пошук границі в дійсній області, complex – пошук границі в комплексній області. Обчислення границі послідовностей здійснюється за допомогою функції limit(f(n),n=infinity),для змінної nможна використати функцію assume(n, integer).
| > assume(n,integer); | |
| > limit((1/n-sin(1/n))*(n^3),n=infinity); | 
|
| > limit((1+1/n)^(7*n),n=infinity); | 
|
| > Limit((1+1/n)^(7*n),n=infinity); | 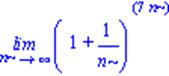
|
| > limit(tan(x),x=Pi/2,left); | 
|
| > Limit(tan(x),x=Pi/2,right); | 
|
| > value(%); | 
|
| > limit(((5-x)/(6-x))^(x+2),x=infinity); | 
|
Обчислення похідних функцій.
Для диференціювання функцій в системі MAPLE використовуються стандартні функції diff(f,x1,x2…xn), Diff(f,x1,x2…xn), деf– алгебраїчний вираз, який диференціюється , зокрема функція змінних x1,x2,….xn. Друга функція Diff представляє собою пасивну форму функції.
Слід зауважити, що при використанні функції diffабо Diffрезультатом обчислення є алгебраїчний вираз, який безпосередньо не може бути обчислений для фіксованих значень аргументів. Для обчислення похідних старших порядків при використанні функцій diff(f,x1,x2…xn), Diff(f,x1,x2…xn)можна використовувати однакові значення аргументів, або використовувати конструкцію x$k, де x – змінна по якій проводиться диференціювання, k – порядок похідної по змінній x, $ - спеціальний символ повтору елементу x k разів.
Другий спосіб обчислення похідних функцій пов`язаний з використанням диференціального оператора D,який має наступний вигляд D(f) або D[i](f), де f – вираз або функція, i - додатне ціле число, вираз, який має ціле значення, або послідовність цілих чисел, яка вказує номери аргументів по яким здійснюється диференціювання функції. На відміну від функції diff(f,x1,x2…xn)операторD[i](f)після обчислення результату диференціювання зразу продукує функцію відповідної кількості аргументів, що дозволяє провести безпосереднє обчислення відповідної похідної для будь – якого значення аргументів.
| >Diff(sin(x)/x,x)=diff(sin(x)/x,x); | 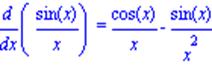
|
| > diff(sin(x)/x,x$3); | 
|
| > diff(sin(x)/x,x,x,x); | 
|
| > g:=sin(x)/x+tan(x); | 
|
| > diff(g,x); | 
|
| >diff(x*y/sqrt(1+x^2+y^2),x,x)+ diff(x*y/sqrt(1+x^2+y^2),y,y); | 
|
| >f:=(x,y,z)->sin(x*y*z); | 
|
| >g1:=D[1,2,2](f); | 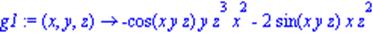
|
| > g1(1,1,Pi); | 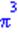
|
| > D(D(D(arctan))); | 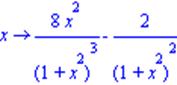
|
Обчислення похідних для функцій заданих параметрично та неявно заданих функцій.
Нехай функція однієї змінної задана параметрично тобто у вигляді  , де змінна t єпараметром. Сама похідна функції, заданої параметрично також задається параметрично і визначається з системи рівнянь:
, де змінна t єпараметром. Сама похідна функції, заданої параметрично також задається параметрично і визначається з системи рівнянь: 
Для знаходження першої похідної параметрично заданої функції зручно створити процедуру користувача Pdiff.
| Pdiff:=proc(y,x) local t; t-> diff(y(t),t)/diff(x(t),t) end proc; | Pdiff := proc (y, x) local t; proc (t) options operator, arrow; diff(y(t), t)/diff(x(t), t) end proc end proc |
Описати параметрично задану функцію
| > x:=t->2*t-t^2; | 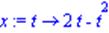
|
| > y:=t->3*t-t^3; | 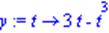
|
Застосувати процедуру Pdiff для обчислення першої похідної
| > f:=Pdiff(y,x)(t); | 
|
Для обчислення похідної більш високого порядку застосувати функцію декілька разів.
| > simplify(Pdiff(Pdiff(y,x),x)(t)); | 
|
| > simplify(Pdiff(unapply(f,t),x)(t)); | 
|
Обчислення похідних від неявно заданих функцій.
Дуже часто виникає необхідність обчислювати похідні від неявно заданих функцій, тобто таких функцій, які задаються у вигляді одного або декількох рівнянь, які містятять як незалежні змінні, так і саму функцію. При заданні неявної функції слід обов`язково визначити які змінні є незалежними, а які є функціями. Для обчислення похідних від неявно заданих функцій використьвується функція implicitdiff( ).Яка може мати один з можливих форматиів:
Читайте також:
- V. СПРОЩЕННЯ ЗОБРАЖЕНЬ
- Використання виразів у запитах
- Додаток 4. Спрощення в групах приголосних
- Імпорт графічних об'єктів і команда Об'єкт WordArt
- Інтегрування виразів, що містять тригонометричні функції
- Команда ERASE (Стерти)
- Команда MIRROR(Дзеркало)
- Команда Автофільтр виконує відбір записів за критеріями одного поля.
- Команда із ОЗП
- Команда із ОЗП
- Команда проекту
- КОМАНДА ПРОЕКТУ
| <== попередня сторінка | | | наступна сторінка ==> |
| Команди перетворення виразів | | |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |