Внутрішні сили при плоскому згині.

При плоскому поперечному згині у загальному випадку в довільних точках перерізів балки виникають нормальні ( 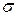) та дотичні ( 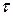) складові напруження, які зводяться до двох внутрішніх силових факторів (зусиль): згинаючого моменту і поперечної сили .

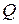Поперечна сила ( 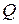) є рівнодійною усіх дотичних складових внутрішніх сил у поперечному перерізі балки. Поперечна сила вважається додатною, якщо вона намагається повернути розглядувану частину балки за ходом годинникової стрілки, і від‘ємною, якщо намагається повернути розглядувану частину балки проти ходу годинникової стрілки (рис. 4.2,а).

Згинаючий момент ( ) є моментом усіх нормальних складових внутрішніх сил у поперечному перерізі балки відносно нейтральної лінії (осі 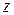). Згинаючий момент вважається додатним, якщо він спричинює розтягання нижніх волокон розглядуваної частини балки, і від’ємним, якщо спричинює розтягання верхніх волокон (рис. 4.2,б).

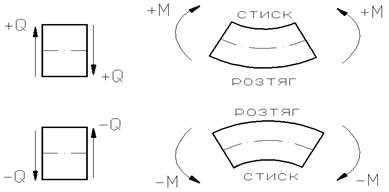
а) б)

Рис. 4.2.

У загальному випадку плоского згину в перерізах балки виникають як згинаючі моменти, так і поперечні сили. Такий згин називають плоским поперечним.

Якщо на якійсь частині балки поперечні сили відсутні ( 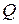=0), то згинаючий момент не цій частині буде постійним ( 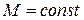). Такий згин називають чистим плоским.

Для визначення поперечних сил і згинаючих моментів, як і для визначення любих внутрішніх сил, застосовується метод перерізів. На основі цього методу маємо такі правила для визначення 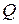і :

1. Поперечна сила ( 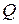) у поперечному перерізі балки дорівнює алгебраїчній сумі проекцій на нормаль до осі балки усіх зовнішніх сил, розташованих по один бік від розглядуваного перерізу. При цьому у виразі для визначення 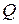додатними вважаються ті зовнішні сили, які намагаються повернути розглядувану частину балки відносно перерізу за ходом годинникової стрілки.

2. Згинаючий момент у поперечному перерізі балки дорівнює алгебраїчній сумі моментів від усіх зовнішніх сил, розташованих по один бік від розглядуваного перерізу, взятих відносно головної центральної осі 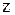(нейтральної лінії). При цьому додатними у виразі для вважаються моменти від зовнішніх сил, які викликають розтягання нижніх волокон балки.

Між згинаючим моментом ( ), поперечною силою ( 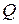) та інтенсивністю розподіленого навантаження ( ) існують наступні диференціальні залежності (теореми Д.І. Журавського):

теорема 1: ;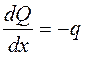

теорема 2: 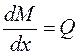; (4.1)

теорема 3: .

Розподілене навантаження інтенсивності вважається додатним при дії зверху вниз.

Для визначення положення небезпечних перерізів балки будують епюри згинаючих моментів і поперечних сил.

Епюрами 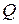і називаються графіки, що зображують закони змінювання 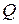і уздовж балки.

Порядок побудови епюр Q і М

1. Визначають опорні реакції балки (для консолі їх можна аналітично не визначати, складаючи вирази для Q і М, як це вже відмічалося раніше, з боку вільного кінця консолі).

2. Балку розділяють на ділянки. Межами ділянок є кінцеві та опорні перерізи балки, а також перерізи, в яких прикладені зовнішні активні зосереджені сили та моменти, або починаються чи закінчуються розподілені навантаження.

3. Для кожної ділянки балки складають аналітичні вирази для визначення Q і М.

4. На основі аналітичних виразів отримують значення Q і М в характерних перерізах балки (межі ділянок, екстремальні значення М, а при необхідності й інші перерізи).

5. Від базових ліній, які паралельні осі балки, відкладають отримані значення Q і М (ординати епюр) у характерних перерізах і орієнтуючись на аналітичні вирази для Q, М будують епюри.

Додатні значення ординат Q відкладаються вверх від базової лінії, а від’ємні – вниз. На епюрах Q завжди необхідно ставити знаки.

Додатні значення ординат М відкладаються вниз, а від’ємні – вверх від базової лінії, тобто епюра М будується з боку розтягнутих волокон. На епюрах М знаки можна не ставити.

Правила контролю правильності побудови епюр Q і М

Правила контролю витікають з теорем Д.І. Журавського (4.1).

1). Якщо на ділянці балки немає розподіленого навантаження (інтенсивність q = 0), то на цій ділянці поперечна сила стала (Q = const), а згинаючий момент М змінюється за законом прямої лінії (епюра Q обмежена прямою лінією, паралельною базовій лінії, а епюра М обмежена похилою прямою).

2). Якщо на ділянці балки діє рівномірно розподілене навантаження (інтенсивність q=const), то на цій ділянці Q змінюється за законом прямої лінії (епюра Q обмежена похилою прямою), а М змінюється за законом квадратної параболи, опуклість якої звернена в бік діючого навантаження.

3). Якщо на ділянці балки діє розподілене навантаження, то в перерізі балки, де Q=0, згинаючий момент М має екстремальне значення. Причому, якщо Q (розглядаючи епюру зліва направо) плавно змінює знак з “+” на “–“, то в згаданому перерізі реалізується в алгебраїчному розумінні М_max, якщо ж Q змінює знак з “–“ на “+”, то реалізується - М_min.

4). Початок та кінець розподіленого навантаження на епюрі Q реалізується у вигляді зламу, а на епюрі М – у вигляді плавного переходу від прямої до кривої лінії або від кривої лінії до кривої.

Наступні правила (5-7) дійсні при розгляді епюр Q і M зліва направо.

5). Якщо на ділянці балки Q має додатне значення (Q > 0), то М зростає (в алгебраїчному розумінні), якщо ж Q < 0, то М зменшується.

6). У точці, яка відповідає прикладанню зосередженої сили, на епюрі Q буде стрибок на величину та в напрямі дії сили, а на епюрі М буде перелом, вістря якого направлене в бік діючої сили.

7). У точці, яка відповідає прикладанню зосередженого моменту, на епюрі М буде стрибок на величину прикладеного моменту, згідно з його напрямком, а на епюрі Q ніяких змін не буде.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
РОЗРАХУНОК СТАТИЧНО ВИЗНАЧЕНИХ БАЛОК НА МІЦНІСТЬ ПРИ ПЛОСКОМУ ЗГИНІ	\|	Небезпечні перерізи балки

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.01 сек.