
МАРК РЕГНЕРУС ДОСЛІДЖЕННЯ: Наскільки відрізняються діти, які виросли в одностатевих союзах
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
Контакти
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Напруженість як градієнт потенціалу
Розглянемо випадок переміщення одиничного додатнього точкового заряду q iз точки 1 в точку 2 вздовж осі x.
| qo |
| x1 |
| x2 |
| x |
Елементарна робота по переміщенню цього заряду дорівнює :
 ,
,  .
.
Ця ж сама робота дорівнює різниці потенціалів :
dА=j1-j2= -dj.
Прирівнявши праві частини обох виразів , одержимо :
 ,
,
тобто проекція вектора напруженості електростатичного поля на вісь х визначається швидкістю зміни потенціалу у напрямку х.
Аналогічно можна одержати, що:
 та
та  .
.
Додавши праві та ліві частини цих рівнянь і домноживши їх на одиничні вектори
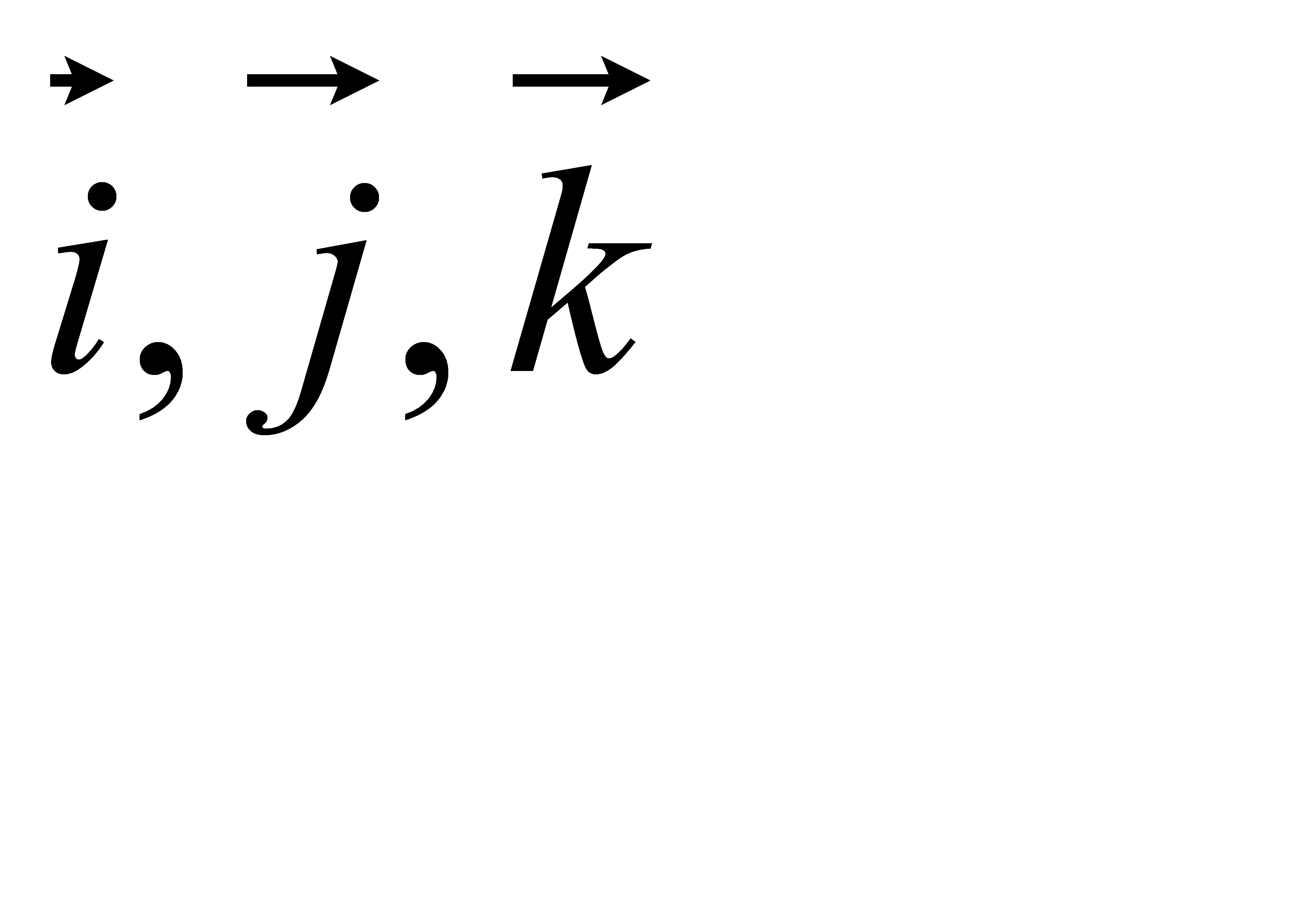 (орти) , одержимо :
(орти) , одержимо :
 .
.

|

|
Або :
 .
.
 - вектор градієнта потенціалу чисельно дорівнює швидкості зміни потенціалу поля на одиницю довжини.
- вектор градієнта потенціалу чисельно дорівнює швидкості зміни потенціалу поля на одиницю довжини.
Знак “мінус” означає , що вектор  спрямований в сторону зменшення потенціалу.Уявна поверхня , всі точки якої мають одинаковий потенціал, зветься поверхнею рівного потенціалу, або еквіпотенціальною поверхнею. Її рівняння має вигляд j(x,y,z)= const. При переміщені по дотичній до еквіпотенціальної поверхні на відрізок
спрямований в сторону зменшення потенціалу.Уявна поверхня , всі точки якої мають одинаковий потенціал, зветься поверхнею рівного потенціалу, або еквіпотенціальною поверхнею. Її рівняння має вигляд j(x,y,z)= const. При переміщені по дотичній до еквіпотенціальної поверхні на відрізок  потенціал не змінюється (dj=0). Так як
потенціал не змінюється (dj=0). Так як  , то проекція вектора
, то проекція вектора  на дотичну ліню дорівнює нулю. А це означає, що вектор
на дотичну ліню дорівнює нулю. А це означає, що вектор  перепендикулярний до еквіпотенціальної поверхні.
перепендикулярний до еквіпотенціальної поверхні.
Отже, лінії напруженості електростатичного поля у кожній точці перпендикулярні до еквіпотенціальних поверхонь.
За допомогою формули  (або
(або  ) по відомій величині напруженості поля можна знайти різицю потенціалів між двома довільними точками поля.Розглянемо декілька прикладів:
) по відомій величині напруженості поля можна знайти різицю потенціалів між двома довільними точками поля.Розглянемо декілька прикладів:
а) Поле безкінечної рівномірної зарядженості площини:
 ;
;  – поверхнева густина зарядів ;
– поверхнева густина зарядів ;  .
.
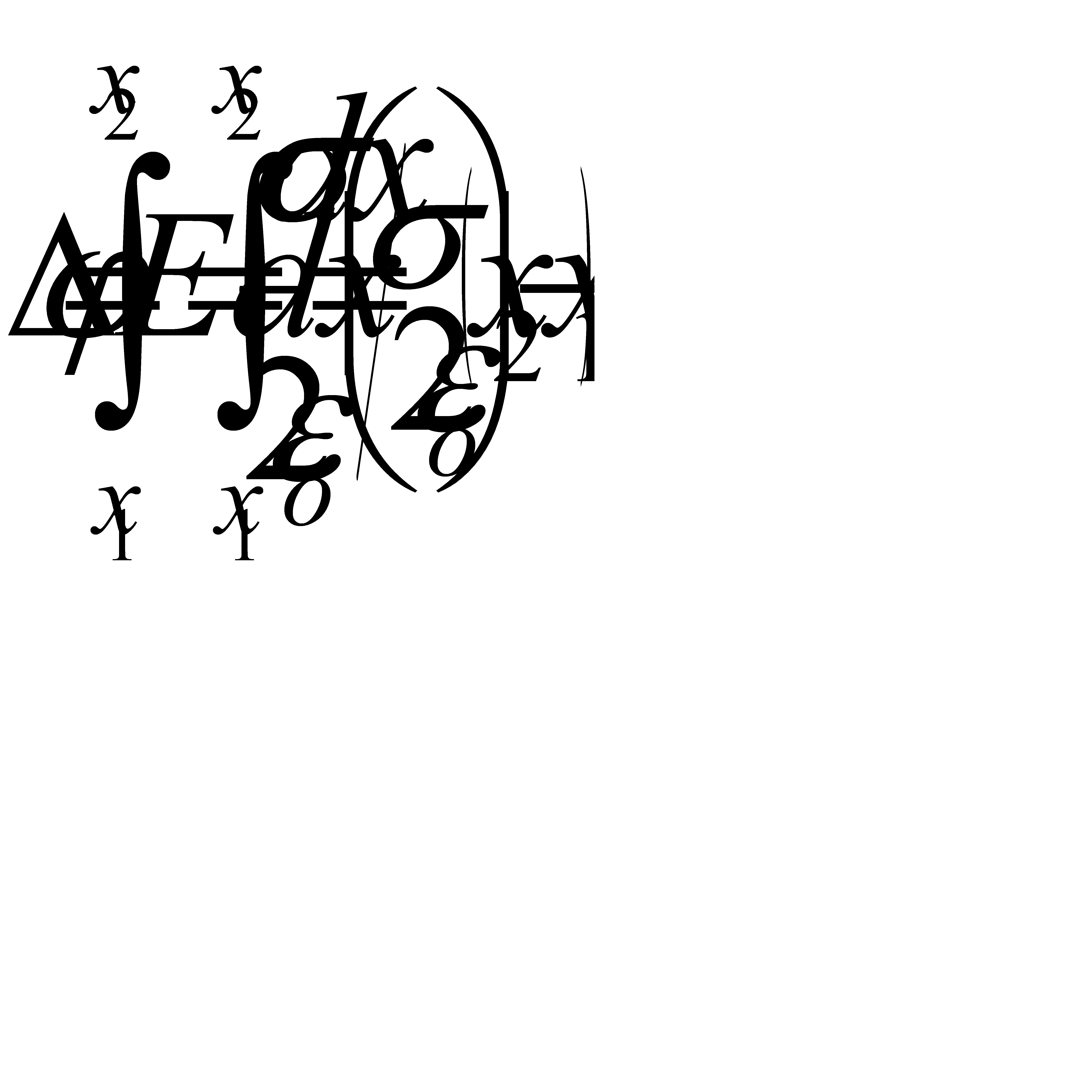
 .
.
Рис.11
 Якщо
Якщо  (див. рис.3) ,
(див. рис.3) ,  .
.
| d |

|
| х |

|

|
Рис. 3
б) Нехай поле створюється пустотілою сферичною поверхнею радіуса R (рис.4).
При r<R E=0 (за теоремою Остроградського-Гауса)
При r³R  .
.
| r |
| E |
| R |

| R |




 .
.
Рис.12 Рис.13
Якщо r1=R , а r2= ¥ , то потенціал зарядженої сфери j= q/ 4пe0R ;
в) Нехай поле створюється зарядженою кулею радіуса R (рис.6).
Якщо z¢<R :
а)  (всередині кулі);
(всередині кулі);
 .
.
б) Якщо  ,
,  , тоді ;
, тоді ; 
(так само ми для точкового заряду або пустотілої сфери !).

| R |
| r |
| E |


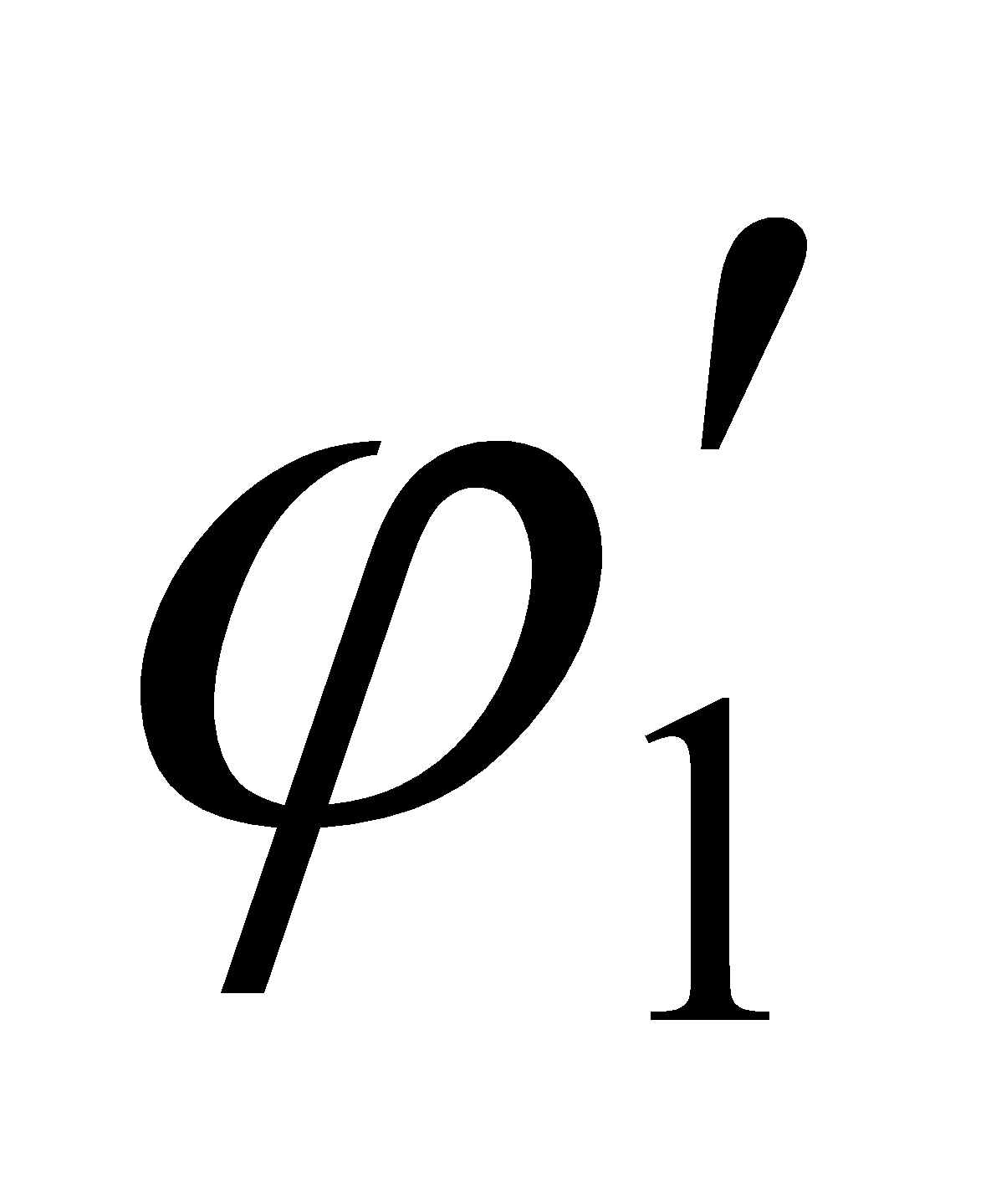





| R |
Рис.14 Рис.15
Лекція №9
Читайте також:
- Автоматія серця. Градієнт автоматії. Дослід Станіуса.
- Алгоритм формування потенціалу Ф2
- Аналіз трудового потенціалу
- Важкість праці: Динамічні, статичні навантаження. Напруженість праці. Увага, напруженість аналізаторних функцій, емоційна та інтелектуальна напруженість, монотонність праці.
- Вертикальний градієнт температури
- Визначення градієнту зміни швидкості.
- Вимірювання величини виробничого потенціалу підприємства на базі поелементного підходу.
- Витратна концепція оцінки потенціалу підприємства
- Витратна концепція оцінки потенціалу підприємства
- Властивості градієнта
- Внутрішньоорганізаційне навчання як технологія розвитку кадрового потенціалу організації
- Вплив факторів природно-ресурсного потенціалу на галузеву та територіальну структуру господарства регіону.
| <== попередня сторінка | | | наступна сторінка ==> |
| Потенціал j в будь-якій точці електростатичного поля це фізична величина, яка визначається потенціальною енергією одиничного додатнього заряду, поміщеного в цю точку поля. | | | Провідники у електростатичному полі |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |