• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Визначення градієнту зміни швидкості.

У чисельній схемі методу молекулярної динаміки використовується друга похідна від координати по часу, тобто прискорення:

,

.

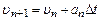Оскільки моделювання розглядається в наближенні класичної динаміки, то можна використати другий закон Ньютона

.

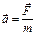де 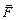– сила, що діє на частинку масою .

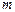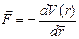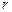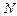Зробимо припущення, що частинки системи - хімічно інертні кульки і сила взаємодії будь-яких двох з них залежить лише від відстані між ними. Тоді , - потенціал взаємодії двох частинок на відстані . Повна потенціальна енергія системи, що містить частинок, визначається сумою двочастинкових взаємодій всіх частинок

,

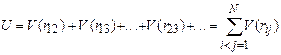де залежить лише від абсолютної відстані 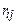між частинками 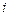та 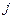. Парна взаємодія такого виду відповідає “простим” рідинам, наприклад рідкому аргону.

Важливими особливостями потенціалу є сильне відштовхування на малих відстанях 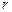і слабке притягання на великих. Наприклад, на атомному рівні відштовхування при малих 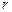зумовлене правилом заборони: якщо електронні хмаринки двох атомів перекриваються, деякі електрони повинні збільшувати свою енергію, щоб знаходитися в різних квантових станах - сумарний ефект проявляється у відштовхуванні між електронами, яке називається відштовхуванням кора. Слабке притягання при великих 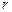зумовлено взаємною поляризацією атомів - результуюча сила притягання називається силою Ван-дер-Ваальса.

Кожна конкретна модель має свій рецепт визначення градієнта зміни швидкості. Наприклад, для моделі з гармонічним осцилятором враховується сила пружності за законом Гука, для моделі польоту тіла під кутом до горизонту визначаються проекції сил на кожну з осей за законами механіки. У деяких моделях градієнтом може бути не швидкість руху частинки в буквальному сенсі. Наприклад, при моделюванні вистигання тіла це коефіцієнт пропорційності у законі теплопровідності.

При моделюванні системи з багатьох частинок для визначення сили взаємодії між частинками використовують більш формальний підхід і визначають силу, а через неї й прискорення, як похідну енергії по координаті. Серед найбільш вживаних феноменологічних формул – потенціал Ленарда-Джонса та потенціал Борна-Майєра.

Читайте також:

1. I визначення впливу окремих факторів
2. II. Визначення мети запровадження конкретної ВЕЗ з ураху­ванням її виду.
3. II. Мотивація навчальної діяльності. Визначення теми і мети уроку
4. IV. Критерій питомої потенціальної енергії деформації формозміни
5. Ocнoвнi визначення здоров'я
6. А. Без зміни хазяїна та ендогенної агломерації
7. А. Без зміни хазяїна та ендогенної агломерації
8. АДАПТАЦІЯ ОПЕРАЦІЙНОЇ СИСТЕМИ ДО ЗМІНИ ЇЇ ЗАВАНТАЖЕННЯ.
9. Адміністративні зміни кінця 18-19 ст. та утворення нових архівів
10. Адміністративно-політичний устрій Української козацької держави середини XVII ст. Зміни в соціально-економічних відносинах
11. Адміністративно-політичний устрій Української козацької держави середини XVII ст. Зміни в соціально-економічних відносинах
12. Алгебраїчний спосіб визначення точки беззбитковості

Переглядів: 1056