• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Найбільш поширені символи

= дорівнює, результат дії.

≡ збігається, конкурує.

|| паралельність.

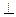перпендикулярність.

◦ . мимобіжність.

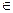належить, є елементом.

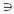проходить, включає в собі.

∩ перетин (прямих, площин).

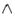відповідає сполучникам „і”, „та”.

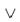відповідає сполучникам „або”, „чи”.

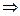логічний наслідок.

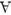квантор спільності.

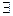квантор існування.

{...} сукупність або складається зі...

α^β кут, кут між площинами α та β.

н.в. натуральна величина.

Вступ

Нарисна геометрія – розділ геометрії, в якому просторові фігури, що являють собою сукупність точок, ліній, поверхонь, вивчаються за їх проекційним відображенням, або – це розв'язання математичної задачі в графічній інтерпретації.

Одна із головних задач нарисної геометрії – створення методу відображення тривимірних фігур на площину та розробка способів розв'язання позиційних та метричних задач, пов'язаних з цими зображеннями, що розвиває просторову уяву.

Нарисна геометрія є теоретичною базою для створення креслення. Креслення – своєрідна мова, за допомогою якої, використовуючи точки, лінії, обмежене число знаків та цифр, людина має змогу зобразити на поверхні, частково, на площині геометричні фігури або їх сполучення (машини, пристрої, споруди).

Методи нарисної геометрії находять своє застосування в авіаційній та машинобудівній промисловості при створенні корпусів літаків, суден, а також в інших областях техніки, в архітектурі, будівництві, образотворчому мистецтві. Різноманітні форми рельєфу земної поверхні при проектуванні доріг, каналів, тунелей, земельних робіт можна зображати на площині. Математичні задачі в графічній інтерпретації знаходять своє застосування у фізиці, хімії, механіці, кристалографії і т.п.

Читайте також:

1. II. Критерій найбільших лінійних деформацій
2. V. НАЙБІЛЬШ ВАЖЛИВІ ПОДІЇ І ДАТИ
3. А. Логічні символи
4. Алгоритм знаходження найбільшого та найменшого
5. АТ – одна з найбільш зручних форм колективного підприємства в умовах ринкової економіки. Першим АТ вважають створену у 1602 році Голандсько –Ост - Індську компанію.
6. Банківський кредит — найпоширеніша форма кредиту. Об'єктом банківського кредиту є грошовий капітал.
7. В межах наукового підходу існує велика кількість концепцій, але найбільш переконлива – еволюційна теорія.
8. ВЕЛИКОБРИТАНІЯ НАЙБІЛЬШ РОЗВИНЕНА НІЖ ІТАЛІЯ
9. Випишіть 3 партії, що на вибораз 1994р. набрали найбільшу кількість голосів, зазначте прізвища їх лідеорів, яку ідеологію вони ісповідували?
10. Відносно фронтальної площини проекцій модель треба розташувати так, щоб на цю площину вона спроекціювалась найбільш наочно – це зображення є головним виглядом.
11. Відомості про найбільші озера Світу та України.
12. Відомості про найбільші озера Світу та України.

Переглядів: 602