• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Поверхні з двома напрямними

(Поверхні Каталана)

Каталан – бельгійський математик, який досліджував властивості цих поверхонь.

Ці поверхні утворюються рухом прямої лінії, яка для всіх своїх положень зберігає паралельність деякій заданій площині (площина паралелелізма) та перетинає напрямні. До них відносять: циліндроїд, параболоїд, коноїд.

1. Гіперболічний параболоїд (коса площина) – використовується в інженерно-будівній практиці при формуванні поверхонь укосів та насипів (рис. 68 ).

Рисунок 68 – Гіперболічний параболоїд

2. Коноїд – поверхня використовується в гідротехнічному будівництві для формування будівництва поверхні підвалин мостових опор (рис. 69).

Задача: Відомо, що т. А та В належать поверхні коноїда (рис. 69), але на кресленні задані лише їх проекції – А₁ та В₂. Побудувати відсутні проекції – А₂ та В₁.

Пояснення до побудов проекцій точок А₂ та В₁.

1. Із двох проекцій більш просто будується проекція т. В – В₁. Проводять через В₂ твірну l, паралельну α₂. Визначають перетин твірної l^і з напрямними m та n. Знаходять відсутню проекцію твірної l^і, куди на неї проекціюють точку В.

Рисунок 69 – Коноїд

2. Відсутню проекцію точки А (А₂) будують за рахунок введення допоміжної січної площини β (β┴П₁).

Ця площина перетинає поверхню коноїда по кривій а, на яку і проекціюємо відсутню проекцію точки А.

3. Циліндроїд має застосування у повітроводах великих діаметрів (рис. 70).

а) циліндроїд б) повітровід, поверхня якого є циліндроїдом

Рисунок 70 - Циліндроїд та його використання

Загальний визначник цих поверхонь:

Ø (l, m, n, α),

m, n –напрямні; lװα,

α– площина паралелізму. α – займає певне положення.

Нижче ознайомтесь з геометричною та алгоритмічною частинами визначників поверхонь, що показані, відповідно, на рис. 68 – 70.

1 Гіперболічний параболоїд:

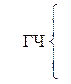
m ,n – напрямні,прямі; lװα;

l – твірна; l∩m, n;

α – площина паралелізму. α ^П₁.

2 Коноїд:

m – напрямна, пряма; lװα ;

n – напрямна, крива; l∩m,n;

l – твірна; αװ П₁.

a – площина паралелізму.

3 Циліндроїд:

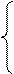l – твірна; l׀׀α;

ГЧ m,n – напрямні, криві; l∩ m,n;

α – площина паралелізму. α ^П₁.

Отже, якщо слід побудувати одну із поверхонь Каталана, то необхідною умовою є задання геометричної частини визначника будь-якої із цих поверхонь та положення площини паралелелізму. Відсутні проекції точок, що належать цим поверхням, можна будувати :

а) за допомогою проекції твірної, використовуючи алгоритмічну частину визначника поверхні;

б) за допомогою січної площини (якщо для заданої проекції точки неможливо застосувати алгоритмічну частину визначника), яка перетинає твірні, що знаходяться поблизу заданої проекції точки.

Читайте також:

1. Алгоритм розрахунку температури поверхні чипу ІМС процесора
2. В'язкості і тиску повітря від профілю тіла, стану його поверхні і положення тіла в повітряному потоці.
3. Великої питомої поверхні пилинок (відношення площі поверхні до їх
4. ВИЗНАЧЕННЯ МІНІМАЛЬНОГО ЗНАЧЕННЯ ТЕМПЕРАТУРИ НА ВНУТРІШНІЙ ПОВЕРХНІ
5. Визначення напруг на похилих площадках. Умови на поверхні
6. Визначення температури на поверхні ізоляції принадземномупрокладанні та при прокладанні трубопроводів в приміщенні.
7. ВИЗНАЧЕННЯ ТЕМПЕРАТУРНОГО ПЕРЕПАДУ МІЖ ТЕМПЕРАТУРОЮ ВНУТРІШНЬОГО ПОВІТРЯ І ПРИВЕДЕНОЮ ТЕМПЕРАТУРОЮ ВНУТРІШНІЙ ПОВЕРХНІ
8. Вимірювання розмірів деталей та шорсткуватості поверхні
9. Вирішити дану проблему у бюджетуванні можна двома основними способами.
10. Виробнича функція з двома змінними факторами
11. Виробнича функція з двома змінними факторами
12. Витрати та надходження за двома інвестиційними проектами

Переглядів: 975