• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

КОМПЛЕКТУВАННЯ МАШИН ЯК СИСТЕМИ МАСОВОГО ОБСЛУГОВУВАННЯ

1. Структура системи масового обслуговування.

2. Потоки вимог.

3. Виведення формули ймовірності простою каналу обслуговування і визначення існих характеристик СМО.

Комплекти машин «кран - панелівоз», «екскаватор – самоскид» можна уподібнювати СМО. В цій системі взаємодіють ведучі і однотипні комплектуючі машини, тобто потік машин – є однорідним потокам вимог.

Ведучі машини називають каналом обслуговування, а комплектуючі – вимогами.

Потоки машин можуть бути:

- замкнуті (з чеканням обслуговування);

- розімкнуті.

По числу каналів: багатоканальні, одноканальні.

Структура СМО

Вхідний потік Вихідний

вимог потік вимог

(машин) (машин)

К_і – канали обслуговування.

Аналітичному розв’язку піддаються найпростіші потоки вимог (стаціонарні чи Пуасоновські потоки)

Ймовірність появлення числа подій в законі Пуасона визначається за формулою

,

де n – число вимог в системі;

– середнє число вимог, що поступають у систему за проміжок часу t

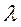- інтенсивність потоку вимог.

Стаціонарний потік вимог називається тому, що a=const, тобто (t)=const, або не залежить від проміжку часу t.

Найпростіший потік володіє також властивостями ординарності і відсутності наслідку. В першому випадку, припускається, що події відбуваються поодинці, тобто ймовірність вступу 2 чи більше вимог в один і той же момент часу мала, тобто нею можна знехтувати.

В потоці з відсутності наслідку припускається, що число вимог, що поступаючи за проміжок часу t₂ не залежить від, того скільки їх поступило за проміжок t₁.

Потоки вимог можуть бути регулярними або випадковими.

Розглянемо графік роботи поста обслуговування з регулярним потоком витрат.

t_n=5хв; і t_pc=20хв; N=20/5=4

1. Простій автосамоскидів у черзі відсутній.

2. Пост обслуговування завантажений повністю.

Розглянемо роботу поста з випадковими вимогами.

tn=5хв; tpc=20хв; tpc=20+-2,5хв

Простої – прямий наслідок розсіювання вхідних даних – наслідок стохастичності.

Розглянемо таку задачу:

Припустимо, що в системі, з найпростішим потоком вимог, їх кількість дорівнює «m». Потрібно визначити ймовірність Рn того, що в системі знаходиться «n» вимог, і також ймовірність Ро того, що в системі знаходиться «о»вимог. Щоб записати систему лінійних диференціальних рівнянь, з розв’язку якої можна буде знайти Рn і Pо, будують розмічений графік стану системи. Кожний стан будемо позначати прямокутником.

Під розміченням станом системи розуміють постановку інтенсивності потоку вимог над стрілкою, з’єднуючі відповідний стан системи.λ

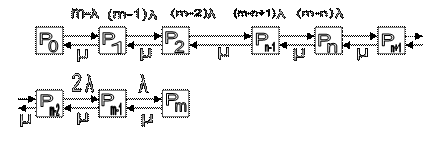
Ро –

Рn – ймовірність того, що в системі о-вимог; n-вимог; m-вимог.

Pm –

Якщо n=0 то в системі нема вимог. Якщо в системі нема вимог, тоді інтенсивність їх прибуття дорівнює добутку ·m.

По розміченому графіку вимог диференціальне рівняння записується на основі наступного символічного (мнемонічного) правила.

1. Похідна ймовірності знаходження системи в стані і дорівнює алгебраїчній сумі декількох доданків. Число доданків дорівнює число стрілок, з’єднуючих стан «і» з другими станами.

2. Якщо стрілки виходять з стану, то вони мають знак «-», якщо входять то знак «+». Кожний доданок дорівнює добутку ймовірності того стану, з якого направлення на інтенсивність потоку подій переведеного стану по заданій :

;

;

;

.

Для встановленого режиму роботи комплекту машин ймовірності станів не залежать від часу, а тому їх похідні дорівнюють «0». Звідси з диференціальних рівнянь отримуємо алгебраїчні рівняння, які дозволяють вивести рекурентну форму, тобто виразити кожну послідовну ймовірність через попередню.

Наприклад: , звідки , або .

Таким чином можна записати:

Рекурентна формула для

визначення ведучих станів

Виконуючи послідовну постановку ймовірностей станів знайдемо Р_n через ймовірність простою каналу обслуговування Р_о.

.

Після перетворення P_n можна записати інакше:

,

де P_n – ймовірність того, що в системі знаходиться «n»вимог, тобто канал обслуговування зайнятий і в черзі знаходиться (n-1) вимога.

Щоб визначити Р_о записуємо додаткову умову:

.

Ймовірність простою каналу обслуговування:

.

Читайте також:

1. I. Органи і системи, що забезпечують функцію виділення
2. I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
3. II. Анатомічний склад лімфатичної системи
4. IV. Розподіл нервової системи
5. IV. Система зв’язків всередині центральної нервової системи
6. IV. Філогенез кровоносної системи
7. POS-системи
8. T. Сутність, етіологія та патогенез порушень опорно-рухової системи
9. VI. Філогенез нервової системи
10. VII. МАШИНОБУДІВНЕ КРЕСЛЕННЯ
11. VІІІ. Проблеми та перспективи розвитку машинобудування.
12. А) Заробітна плата її форми та системи.

Переглядів: 476