• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Розв’язання.

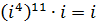
Тут використана періодичність значень іⁿ: і¹ = і, і² = –1, і³ = –і, i⁴ = 1, i⁵ = i і т.д.

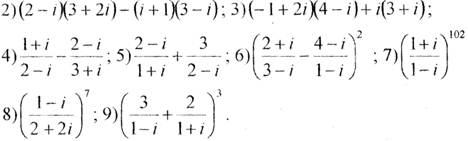
Піднесення до степеня комплексного числа виконується за формулами

zⁿ = |z|ⁿ (cos nφ+ і sin nφ) = |z|ⁿ e^inφ, де φ = arg z.

Корінь n-го степеня із комплексного числа z має п значень, які обчислюються за формулою ,

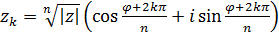, де k = 0, 1, 2, … , (n-1) (3)

Значення, що відповідає k = 0 називається головним або арифметичним значенням кореня.

Завдання 3.Знайти всі значення коренів:

1) .

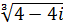Розв’язання.Для обчислення всіх значень 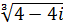скористаємося формулою (3), в якій п = 3, k = 0, 1, 2. Так як |4 – 4i| = = 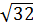= 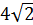, arg(4 – 4і) = 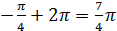, то

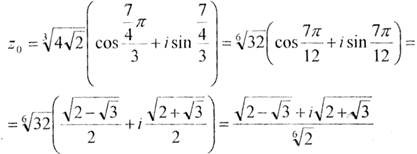
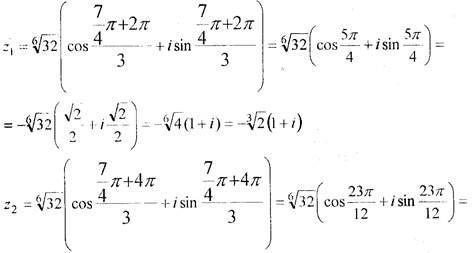
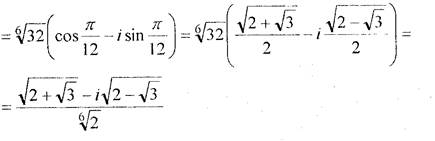
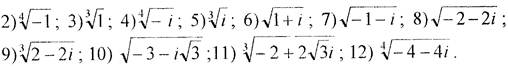
Завдання 4. Знайти множину точок, які задовольняють рівності, і зобразити її на комплексній площині

1)

Розв’язання.Введемо позначення z = х + іу, тоді

.

, ,

, ,

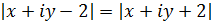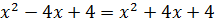8x = 0, x = 0.

Шуканою множиною точок є уявна вісь.

Областю називається відкрита зв’язна множина. Однозв’язиою областю називається область, будь-яку замкнену лінію якої можна деформувати в точку, залишаючись при цьому в даній області.

Завдання5. Знайти множину точок, що задовольняють відповідній нерівності, і зобразити її на комплексній площині

1)

Розв’язання.Введемо позначення z = х + іу і підставимо в умову, одержимо:

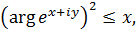
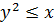– замкнена область, обмежена параболою 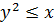(мал. 1).

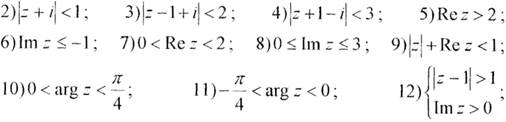
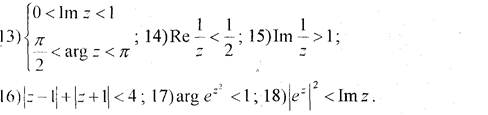
§2. Послідовностітарядикомплекснихчисел.

Послідовність {z_n}, де z_n = x_n + iy_n називається послідовністю комплексних чисел. Для того, щоб ця послідовність мала границю с = = α +iβ, необхідно і достатньо, щоб 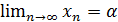, 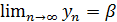. Так як збіжність послідовності комплексних чисел {z_n} зводиться до збіжності двох послідовностей дійсних чисел {х_n} і {у_n}, то всі властивості послідовностей дійсних чисел залишаються в силі і для послідовностей комплексних чисел.

Завдання 6.Знайти границі послідовностей:

.

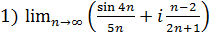Розв’язання.Так як послідовність комплексних чисел {z_n}має границю с = α + іβ, якщо 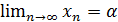та 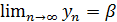,то знайдемо границі і 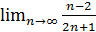. . 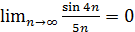Обчислимо границю 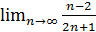, поділивши почленно чисельник та знаменник на п: 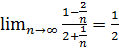. Отже .

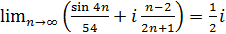Завдання 7.Дати відповідь на наступні питання:

а) Чиіснує скінченна границя послідовності?

б) Чи послідовність обмежена?

в) Яка множина всіх часткових границь послідовності?

1) .

Розв’язання,а) Так як не існує, то границя даної послідовності не існує.

б) Послідовності 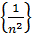та 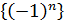обмежені, а тому обмеженою є і задана послідовність.

в) Частковими границями даної послідовності є наступні:

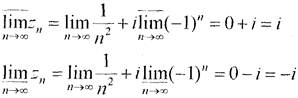
Верхня границя послідовності дорівнює i, а нижня границя дорівнює –i.

Для того, щоб збігався (абсолютно збігався) ряд (1) необхідно і достатньо, щоб збігалися (абсолютно збігалися) ряди (2) i 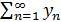(3). При цьому сумою раду (1) буде число a + ib, де а та b суми рядів (2) і (3) відповідно.

Завдання 8.Дослідити на збіжність і абсолютну збіжність ряди:

1) .

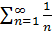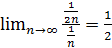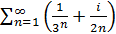Розв’язання.Даний ряд буде збіжним, якщо будуть збіжними такі два ряди дійсних чисел та . Ряд є збіжним, як геометрична прогресія із знаменником q = . Ряд – розбіжний , його можна порівняти з гармонічним рядом . Так як , то із розбіжності гармонічного ряду випливає розбіжність ряду . Отже вихідний ряд розбіжний.

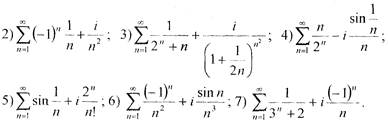
§3. Функціїкомплексноїзмінної. Елементарніфункції.

Якщо кожній точні z з деякої множини Е комплексної площини поставлено у відповідність комплексне число w, то говорять, що на множині Е задана функція w = f(z). Якщо позначити z = x + iy, a w = u + iv, то можна зробити висновок, що задання комплексної функції w = f(z) рівносильне заданню двох дійсних функцій двох змінних и (х, у) та v(x, y): f(z) = u(x ,y) + iv(x, y).

Функція f(z) в точці z₀ = x₀ + iy₀має границю С = А + іВ тоді і тільки тоді, коли функції и(х, у) та v(x, y) в точці (х₀, у₀) мають границі відповідно А та В.

Завдання 9.Чи існує границя функції f(z) в точці z = 0

1)

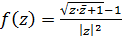
Розв’язання.Для того, щоб знайти 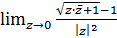домножимо чисельник та знаменник на :

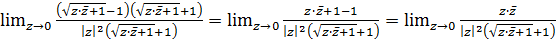
Так як |z|² = х² + у²та 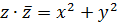, то

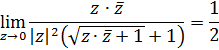
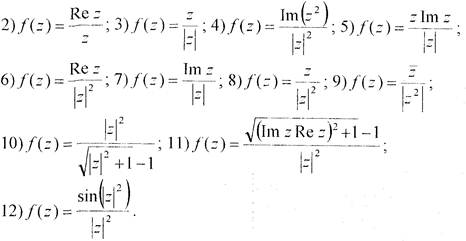
Функція f(z) = U(x, y) + iV(x, y) буде неперервною в точці z₀= = x₀ + iy₀ тоді і тільки тоді, коли будуть неперервними функції двох дійсних змінних U(х, у) та V(x,y) в точці (x₀, y₀).

Завдання10. Дослідити функцію f(z) на неперервність:

1)

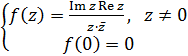
Розв’язання.Дана функція може мати розрив лише в точці z = 0. Якщо 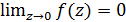, то функція в точці z = 0 буде неперервною. Знайдемо 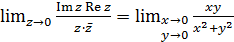. Перейдемо до полярної системи координат х = ρ cosφ, у = ρsinφ, при х → 0та у → 0радіус ρ також прямує до нуля.

Границя даної функції в точці z = 0не існує, так як кут φ може набувати довільного значення із пів сегмента [0; 2π), відповідно sin2φ набуває будь-якого значення із сегмента [–1; 1].

Отже, функція f(z) має розрив в точці z = 0.

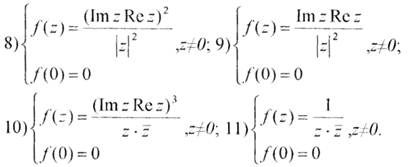
Значення лінійної, дробово-лінійної, степеневої функцій виду zⁿ, 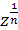(n є Z) обчислюються за відомими правилами дій над комплексними числами. Для показникової функції має місце формула Ейлера е^iг = cosz + isinz. З неї одержуються формули для тригонометричних функцій

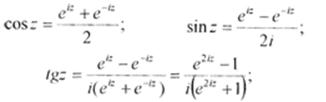
Для гіперболічних функцій мають місце формули аналогічні відомим формулам функцій дійсної змінної

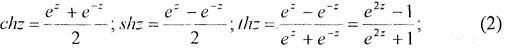
Із показникової форми комплексного числа маємо

За допомогою цих формул показникову функцію a^z та степеневу з довільним показником z^a можна подати так

Обернені до тригонометричних та гіперболічних функцій обчислюються за формулами

Завдання 11.Виділити дійсну та уявну частини числа:

l) .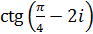

Розв’язання.Щоб виділити дійсну та уявну частини, скористаємося формулою .

Підставимо замість z значення .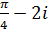

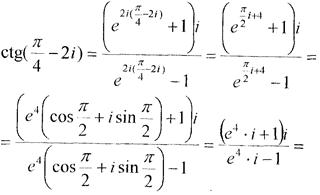
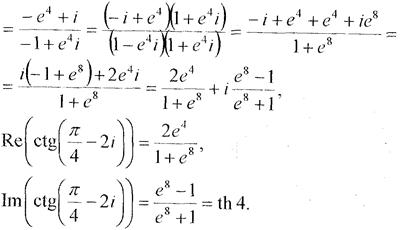
Завдання 12. Розв’язати рівняння

1) sin z = –2i.

Розв’язання.Скористаємося оберненою тригонометричною функцією арксинус: z = Arcsin(–2i). За формулами (4) маємо:

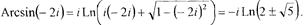
Обчислимо окремо значення та 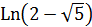, скориставшись формулою (3)

.

Так як

.

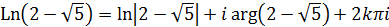Оскільки , то

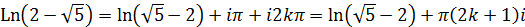
Значення та 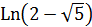об’єднаємо в одне

Отже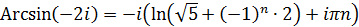

.

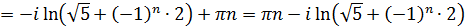Завдання 13.Знайти модуль і головне значення аргумента числа:

1) .

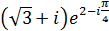Розв’язання.Подамо число 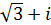в показниковій формі.

Так як 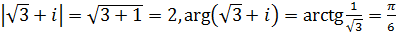, то

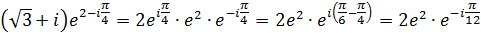
Отже модуль числа 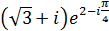дорівнює 2е²,головне значення аргумента цього числа дорівнює .

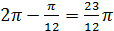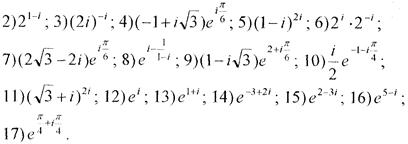
Завдання14. З’ясувати, яку криву визначає комплекснозначна функція від дійсної змінної z(t) і побудувати цю криву.

1) .

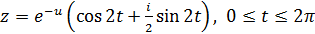Розв’язання.Виділимо в правій і лівій частинах рівності дійсну та уявну частини, тоді

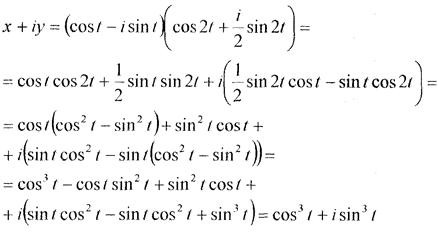
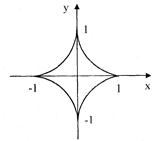Отже х = cos³ t, y = sin³ t, це рівняння астроїди (мал. 2).

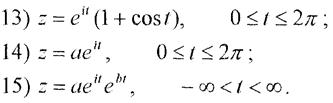
Завдання 15.Довести формули

1) ch²z + sh²z = sh2z.

Розв’язання.Подамо гіперболічні функції shz, chz, sh2z через показникову функцію e^z, скориставшись формулами (2); тоді

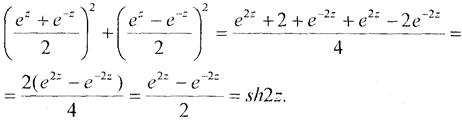
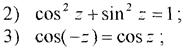
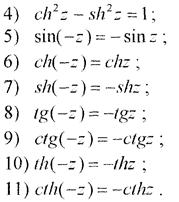
Завдання 16.Довести співвідношення між тригонометричними і гіперболічними функціями

1) cos z - ch iz .

Розв’язання.Скористаємося формулами (1) та (2);

Так як праві частини останніх двох рівностей тотожно рівні, то рівні і ліві, тобто cos z = ch iz.

Завдання 17.Нехай z = x + iy. Довести, що

1) .

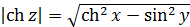Розв’язання.Так як z = х + іу, то

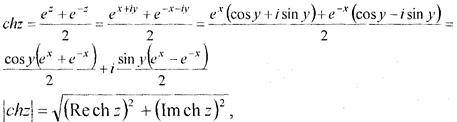
У нас Re ch z = cos y ch x, Im ch z = sin y sh x. Отже,

Так як ch² x – sh²x = l, то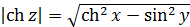

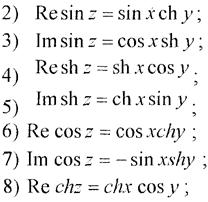
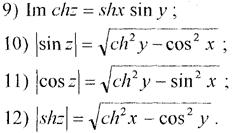
Вказівка:використати формули Ейлера.

Завдання 18.Довести, що функції sinz та cosr необмежені на всій комплексній площині.

§4. Похідна.

Для того, щоб функція f(x + іу) = и(х, у) + iv(x, у) була диференційованою в точці z = х + іу, необхідно і достатньо, щоб функції и(х,у) та v(x,y) були диференційовані по х та у і щоб виконувалися рівності

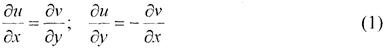
Ці рівності називаються умовами Коші-Рімана. Похідна при цьому може бути обчислена за формулою

Однозначна функція f(z) називається диференційованою в області, якщо вона диференційована в кожній точці цієї області.

Завдання 19. Знайти область диференційовності функції

1) .

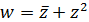Розв’язання.Виділимо дійсну та уявну частини функції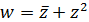

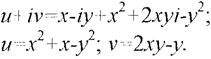
Знайдемо частинні похідні функцій и(х, у) та v(x, y)

Визначимо для яких значень змінних х та у виконуються умови Коші - Рімана (1)

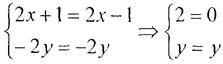
Так як перше рівняння системи розв’язків не має, то не має розв’язків і сама система, а отже задана функція недиференційовна у всій комплексній площині.

Функція u(x, y) називається гармонічною, якщо вона має частинні похідні до другого порядку включно і задовольняє рівнянню Лапласа

Завдання 20.Визначити, чи функція є гармонічною

1) u(х, у) = e^x cos y + x² – у².

Розв’язання.Знайдемо другі частинні похідні та і перевіримо, чи задовольняють вони рівнянню Лапласа (2).

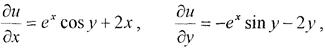
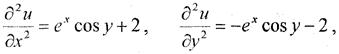
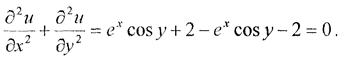
Другі частинні похідні задовольняють рівнянню Лапласа, отже функція u(х, у) = e^x cos y + x² – у² є гармонічною функцією.

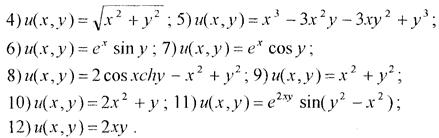
Гармонічні функції, які задовольняють умовам Коші-Рімана, називаються спряженими гармонічними. Дійсна і уявна частина аналітичної функції є спряженими гармонічними функціями. За заданою дійсною (уявною) частиною аналітичної функції можна відновити уявну (дійсну частину) з точністю до довільної сталої

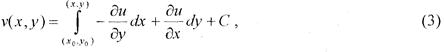
Завдання 21.Побудувати аналітичну функцію f(z) = u(x, y) + + iv(x, y) за її дійсною або уявною частиною.

1) .

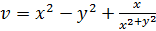Розв’язання.Перевіримо спочатку чи задана функція є гармонічною,

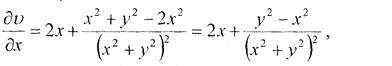
Задана функція є гармонічною, отже можемо побудувати спряжену до неї. Скориставшись формулою (4), будемо мати

Виберемо за точку (х₀, у₀) точку (1,0), тоді

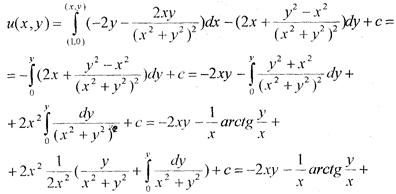
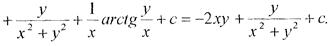
Отже , а функція f(z) дорівнює

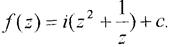
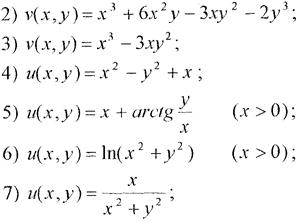
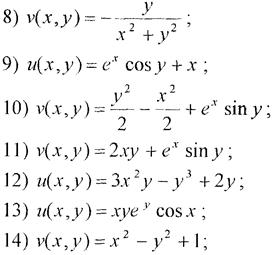
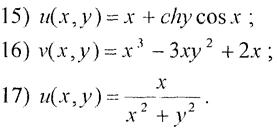
Нехай функція w = f(z) визначена, неперервна в обл. D і w'(z₀) ≠ 0, де z₀є D. Модуль похідної |w(z₀)| визначає коефіцієнт розтягу в околі точки z₀всіх кривих, що проходять через цю точку при відображенні за допомогою функції w = f(z). Аргумент похідної arg(w'(z₀)) визначає кут, на який повертаються всі криві в точці z₀при відображенні w = f(z).

Завдання22. Знайти коефіцієнт розтягу і кут повороту при відображенні за допомогою функції w = f(z) в точці z₀.

l) 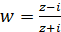, z₀ = 0.

Читайте також:

1. Актуальні проблеми регіональної політики та їх розв’язання.
2. Вказівки до розв’язання.
3. Міжнаціональні відносини і причини виникнення міжнаціональних конфліктів, шляхи їх розв’язання. Міжконфесійні стосунки та їх вплив на життя в полікультурному суспільстві
4. Поняття біосфери та ноосфери. Поняття екології. Основні завдання соціальної екології. Сучасні екологічні проблеми, причини їх виникнення та розв’язання.
5. Розв’язання.
6. Розв’язання.
7. Розв’язання.
8. Розв’язання.
9. Розв’язання.
10. Розв’язання.
11. Розв’язання.
12. Розв’язання.

Переглядів: 7507