• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Розв’язання.

Виходячи із геометричного змісту похідної коефіцієнт розтягу k = |w'(z₀)|, а кут повороту α = arg w'(z₀).

Знайдемо похідну функції 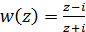і обчислимо її в точці z₀ = 0.

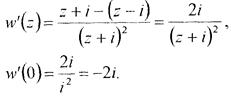
Так як |–2i| = 2 , a arg(–2i) = 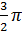, то коефіцієнт розтягу в точці z₀= 0 при відображенні функцією w(z) = 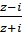дорівнює k = 2, а кут повороту а = .

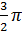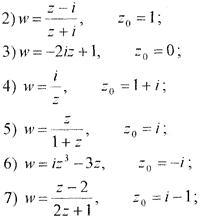
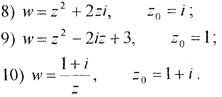
Завдання 23. Яка частина площини стикається при відображенні за допомогою функції w = f(z).

1) w = z³ +2.

Розв’язання. Знайдемо похідну функції w = z³ + 2 та її модуль:

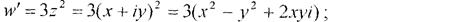
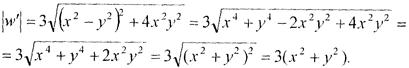
При відображенні за допомогою функції w = f(z) стикається та частина площини, для точок якої виконується умова 0 < к < 1, або 0 < |w'| < 1.

Отже 0 < 3(x² + у²) <1, звідки маємо 0 < х² + у² <

При відображенні за допомогою функції w = z³ + 2 стикається внутрішня частина кола 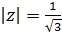з виколотою точкою z = 0.

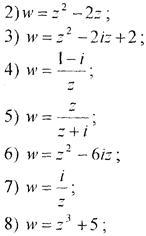
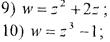
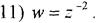
§5. Відображеннязадопомогоюлінійноїфункції.

Функція виду w = az + b , де а, b - сталі комплексні числа, називається лінійною. Відображення за допомогою цієї функції конформне у всій площині (w' = а ≠ 0). Якщо z та а подати у показниковій формі z = ρе^iφ, а = |а|е^iα , то

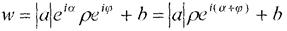
Із останньої рівності слідує, що відображення за допомогою лінійної функції можна розглядати як суперпозицію таких відображень:

1) t = |a|z – розтяг в |a| разів

2) ζ= tе^iα – поворот на кут а проти годинникової стрілки

3) w = ζ + b – паралельне зміщення на b = β₁ +iβ₂.

Завдання 24.Знайти образ на w-площині області при відображенні за допомогою лінійної функції w=az + b.

l) –l < Re z < l

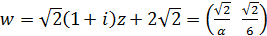
Розв’язання. Знайдемо модуль і аргумент похідної :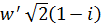

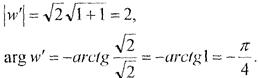
Відображення функцією 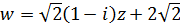є послідовним виконанням таких відображень:

1) t = 2z – розтяг в два рази;

2) 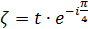– поворот на кут за годинниковою стрілкою;

3) w = 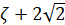– паралельне переміщення.

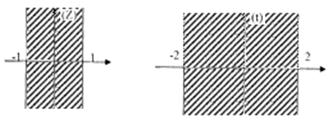
4) Задана область і відображення 1)-3) подані на малюнках 3-6

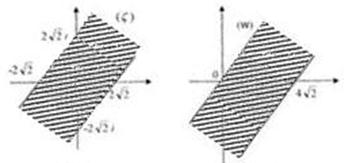
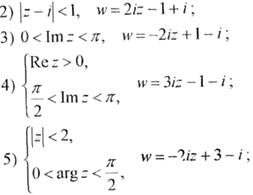
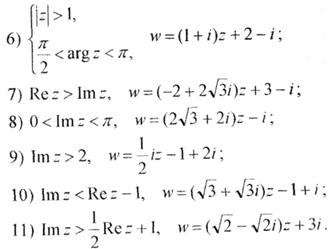
Завдання25. Знайти одну з лінійних функцій, яка відображає область D на z-площині в область G на w-площині:

1) D: |z – 2i| < 1, G: |w – 2| < 2.

Розв’язання.Задані області зображені на малюнках 7-8.

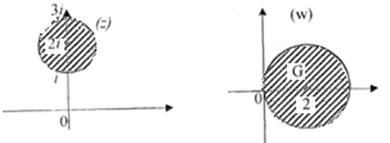
Область D можна відобразити в область G , наприклад, так:

1) t = 2z

2)

3)

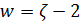
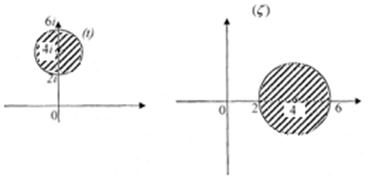
Отже однією з лінійних функцій; що відображає область D на G є наступна:

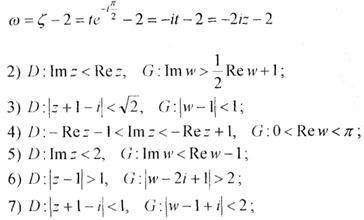
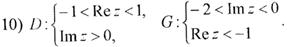
§6. Відображеннязадопомогоюфункції .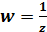

Відображення w = конформне у всіх точках площини за виключенням z = 0 та z = ∞.

При цьому функція всю розширену комплексну площину відображає у всю розширену комплексну площину (точки z = 0 та z = ∞ відображаються відповідно у точки w = ∞ і w = 0).

Функція 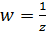володіє круговою властивістю та властивістю збереження симетрії.

Кругова властивість: коло в широкому розумінні функція 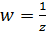відображає у коло в широкому розумінні (колом в широкому розумінні називається коло або пряма у звичайному розумінні).

Властивість збереження симетрії: точки, які симетричні на z-площині відносно кола в широкому розумінні, відображаються у точки симетричні відносно образу цього кола на w-площині.

Точки симетричні відносно прямої - це точки, що лежать на перпендикулярі до цієї прямої і рівновіддалені від неї. Точки M та N симетричні відносно кола з центром в т. О і радіусом R, якщо вони лежать на одному промені, початком якого є точка 0, і задовольняють рівності ОМ · ON = R².

Для здійснення відображення за допомогою функції 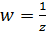запишемо z і w у полярних координатах z = re^iφ, w = ρe^iθ, тоді 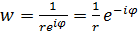, звідки 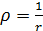; θ = -φ.

Завдання 26.Виконати відображення заданої лінії або області на z-площині за допомогою функції .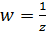

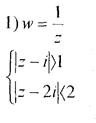
Розв’язання.Виконаємо малюнок заданої області (мал. 11). Для відображення за допомогою функції 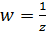скористаємося круговою властивістю цієї функції.

Так як межі заданої області кола |z – і| = 1 та |z – 2i| = 2, проходять через початок координат, то вони відобразяться у прямі.

Пряма виражається двома точками, тому знайдемо образи двох точок кола |z – i| = 1 та образи двох точок кола |z – 2i| = 2:

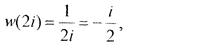
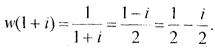
Отже коло |z – і| = 1 відобразиться у пряму Im w = .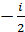

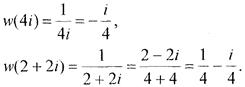
Образом кола |z – 2i| = 2 є пряма Im w = .

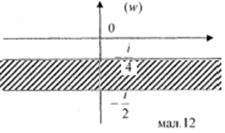Межами образу заданої області D є дві прямі, щоб визначити, чи образ лежить між ними, чи зовні, знайдемо образ будь-якої внутрішньої точки області D. Наприклад z = 3i

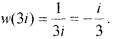
За властивістю конформних відображень внутрішні точки переходять у внутрішні, таким чином образом заданої області є смуга 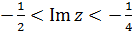(мал. 12)

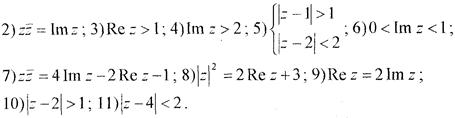
Завдання 27.Відобразити за допомогою функції 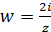область

Завдання 28.Смугу –1 < Re z < 1 відобразити за допомогою функції .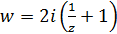

Завдання 29.Знайти конформне відображення області 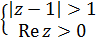у смугу 0 < Im w < 1.

§7. Дробово-лінійнафункція.

Функція виду w 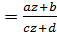(a, b, c, d – сталі числа такі, що с ≠ 0 і ad – bc ≠ 0) називається дробово-лінійною.

Дробово-лінійна функція 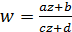всю розширену комплексну площину відображає у розширену комплексну площину.

Для функції 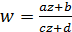виконуються кругова властивість і властивість збереження симетрії наведені в §6.

Існує єдине дробово-лінійне відображення, яке відображає три довільно взяті точки z-площини z₁, z₂, z₂відповідно у три точки w-площини w₁, w₂, w₃. Це відображення визначається рівністю 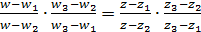яке називається ангармонійним відношенням.

Завдання 30.Знайти образи області D на z-площині за допомогою функції .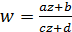

1)

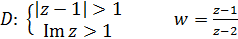
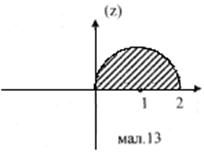
Розв’язання. Виконаємо малюнок області D (мал. 13).

Межами області є коло |z –1| = 1 та пряма Im z = 0. Обидві цілінії проходять через точку z = 2 , в якій знаменник дробу 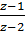перетворюється в нуль.

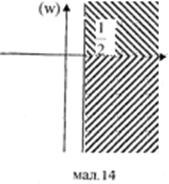За круговою властивістю дробово-лінійної функції коло |z – 1| = 1 і пряма Imz = 0 відобразяться у прямі. Так як пряма визначається двома точками, образи знайдемо двох точок, що належать прямій Imz = 0 : w(0) = , w(3) = 2 Отже дійсна вісь функції 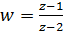відображається у дійсну вісь. Так як коло |z – l| = 1 і дійсна вісь в точці z = 0 взаємно перпендикулярні, то за властивістю збереження кутів при конформному відображенні, образ кола (пряма) в точці w(0) = буде перпендикулярний до дійсної осі.

Рівняння прямої, що є образом кола |z – 1| = 1, буде Rew = .

Точка z = i є внутрішньою точкою області D , тому точка 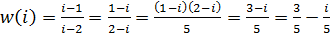є внутрішньою точкою образу області D. Отже образом області D при відображенні функцією 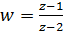буде область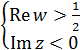

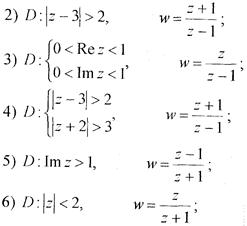
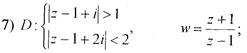
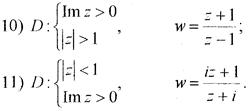
Завдання 31. Знайти конформне відображення верхньої півплощини на нижню, при якому точки 0, 1, ∞ відобража­ються у точки ∞, 1, 0, відповідно.

Розв’язання. Для знаходження дробово-лінійного відображення, яке точки 0, 1, ∞ відображає у точки ∞, 1, 0 відповідно скористаємося ангармонійним відношенням.

Замінивши різниці, в які входить нескінченно віддалена точка, одиницею, одержимо

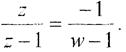
Звідки 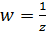. На підставі властивості конформного відображення про збереження обходу при такому відображенні верхня півплощина відображається на нижню півплощину.

Завдання 32. Знайти конформне відображення площини z самої в себе, яке точки z₁, z₂, z₃, переводить відповідно у точки w₁, w₂, w₃.

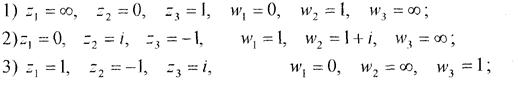
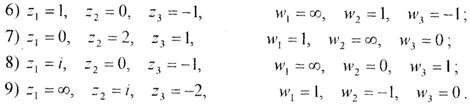
Завдання 33. Відобразити конформно круг |z – l|<2 в круг |w – i| < 2 так, щоб точка О перейшла в центр круга.

Завдання 34. Відобразити конформно півплощину Im z > 1 в круг |z – 2і| < 2так, щоб точка 2i залишилася нерухомою.

Завдання 35. Знайти конформне відображення круга |z| < 2 на півплощину Im w > 0, яке точку О переводить у точку

Завдання 36. Знайти умови, при яких суперпозиція двох дробово-лінійних функцій є:

а) дробово-лінійною функцією;

б) лінійною функцією.

Дослідити чи можливі інші випадки.

§8. Степеневафункціязраціональнимпоказником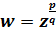

Запишемо функцію 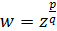наступним чином і розглянемо окремо функції t = z^p та w = t^q.

Похідна функції t = z^p (де pєN) дорівнює t' = pz^p-1і є скінченною, відмінною від нуля у всіх точках площини, крім z = 0 та z = ∞. Відображення цією функцією конформне всюди, крім зазначених точок. Запишемо z та t в полярних координатах z=re^iφ, t = ρе^iθ, тоді із співвідношення t = z^p маємо

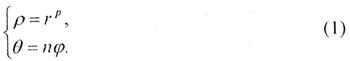
Якщо область задана на z-площині через нерівності для координат r та φ, то за допомогою рівностей (1) знаходимо нерівності для змінних ρ та θ, які визначають образ області у t-площині.

Розглянемо тепер функцію

Як відомо, ця функція не є однозначною, вона складається з q функцій, які знаходяться за формулами (якщо t = pe^iθ)

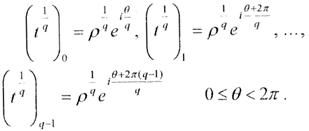
Кожна із вказаних функцій називається відповідною віткою степеневої функції (2).

Відображення функцією 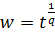виконуються за допомогою формул

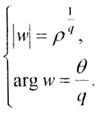
Це відображення площину зрозрізом 0 < θ < 2πпереводить у область 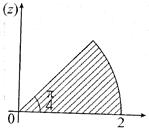кута .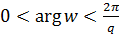

Функція 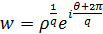відображає другий лист z-площини 2π < θ + 2π < 4π у кут 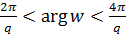на w-площині.

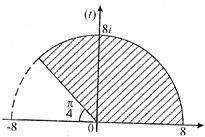
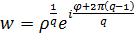Функція відображає q-тий лист z-площини у кут 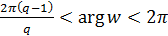на w-площині.

Завдання37. Виконати відображення області D на z-площині за допомогою функції w = f(z)

1) ;

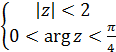w = z³ + 1 + i.

Читайте також:

1. Актуальні проблеми регіональної політики та їх розв’язання.
2. Вказівки до розв’язання.
3. Міжнаціональні відносини і причини виникнення міжнаціональних конфліктів, шляхи їх розв’язання. Міжконфесійні стосунки та їх вплив на життя в полікультурному суспільстві
4. Поняття біосфери та ноосфери. Поняття екології. Основні завдання соціальної екології. Сучасні екологічні проблеми, причини їх виникнення та розв’язання.
5. Розв’язання.
6. Розв’язання.
7. Розв’язання.
8. Розв’язання.
9. Розв’язання.
10. Розв’язання.
11. Розв’язання.
12. Розв’язання.

Переглядів: 3716