
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Методи розробки нелінійних оптимізаційних моделей економічних систем
Для розробкинелінійних оптимізаційних моделей економічних систем вирішуються задачі нелінійного програмування.
Нелінійне програмування - математичні методи визначення максимуму або мінімуму функції за наявності обмежень у вигляді нерівностей або рівнянь. Максимізувавши або мінімізувавши функція є прийнятим критерієм ефективності вирішення задачі, відповідним поставленій меті. В цьому випадку цей критерій має назву цільової функції.
Цільова функція задач нелінійного програмування полягає в тому, щоб знайти умови, що обертають цільову функцію в мінімум або максимум. Рішення, що задовольняє умові задачі і відповідне наміченій меті, називається оптимальним планом. Нелінійне програмування служить для вибору найкращого плану розподілу обмежених ресурсів в цілях вирішення поставленої задачі. В загальному вигляді постановка задачі нелінійного програмування зводиться до наступного. Умови задачі представляються за допомогою системи нелінійних рівнянь або нерівностей, що виражають обмеження, які накладається на використання наявних ресурсів.
В загальному вигляді математична модель задачі нелінійного програмування формулюється наступним чином:
f =(x1,x2, …,хn) → min (max). (6.1)
При цьому ці змінні повинні задовольняти обмеженням:
 g1(x1,x2, …,хn) ≤b1,
g1(x1,x2, …,хn) ≤b1,
…………………………
gm(x1,x2, …,хn) ≤bm,
gm+1(x1,x2, …,хn) ≥bm+1,
…………………………(6.2)
gk(x1,x2, …,хn) ≥bk,
gk+1(x1,x2, …,хn)=bk+1,
………………………
gp(x1,x2, …,хn)=bp.
x1,x2,…,хn ≥0, де одна із функцій f, gi нелінійна.
Для задач нелінійного програмування немає єдиного методу вирішення. Залежно від виду цільової функції і системи обмежень розроблені спеціальні методи вирішення, до яких відносяться метод множників Лагранжа, градієнтні методи, наближені методи вирішення, графічний метод.
Розглянемо деякі з них. Основні ідеї графічного методу: максимум і мінімум досягається в точках дотику лінії рівня з областю допустимих рішень, яка задається системою обмежень. Наприклад, якщо лінії рівня - прямі, то точки дотику можна визначити, використовуючи геометричне значення похідної.
Розглянемо на прикладах вирішення задач нелінійного програмування.
1. Знайти екстремуми функції L(x1,x2)=x1+2x2 при обмеженнях
 ,
,  .
.

| |
Область допустимого вирішення – це частина кола з радіусом 5, яка розташована в I чверті. Знайдемо лінії рівня функції L: x1+2x2=C. Виразимо x2=  . Лініями рівня будуть паралельні прямі з кутовим коефіцієнтом, який дорівнює -
. Лініями рівня будуть паралельні прямі з кутовим коефіцієнтом, який дорівнює -  . Мінімум функції досягається в точці (0;0), Lmin=0, оскільки градієнт
. Мінімум функції досягається в точці (0;0), Lmin=0, оскільки градієнт  (1,2) спрямовано вверх вправо. Максимум досягається в точці дотику кривої х2=
(1,2) спрямовано вверх вправо. Максимум досягається в точці дотику кривої х2=  та лінії рівня. Оскільки кутовий коефіцієнт дотику до графіку функції дорівнює -
та лінії рівня. Оскільки кутовий коефіцієнт дотику до графіку функції дорівнює -  , знайдемо координати точки дотику, використовується геометричне значення похідної.
, знайдемо координати точки дотику, використовується геометричне значення похідної.
 =-
=-  ; (
; (  )
)  =-
=-  ;
;
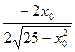 =-
=-  ;
;  x0=
x0=  ; x2=2
; x2=2  .
.
Тоді L=  +2∙2
+2∙2  =5
=5  .
.
Відповідь: Мінімум досягається в точці О(0;0), глобальний максимум, дорівнює 5  , в точці А(
, в точці А(  ;2
;2  ) .
) .
2. Знайти екстремуми функції L=(x1-6)2+(x2-2)2 при обмеженні
 x1+x2≤8
x1+x2≤8
3 x1+x2 ≤15
x1+x2 ≥1
 .
.
 Вирішення
Вирішення
Область допустимого вирішення – багатокутник ABCDE. Лінії рівня представляють собою окружність (x1-6)2+(x2-2)2=С з центром в точці О1(6;2). Візмимо, наприклад, С=36, бачимо, що максимум досягає в точці А(0;4), яка лежить на окружності найбільшого радіусу, який пересікається з областю допустимого вирішення L(A)=(0-6)2+(4-2)2=40. Мінімум - в точці F, яка знаходиться на перетені прямої 3x1+x2 =15 і перпендикуляру до цієї прямої, виведеного із точки О1. Оскільки кутовий коефіцієнт дорівнює -3, то кутовий коефіцієнт перпендикуляру дорівнює  . Із рівняння прямої, яка проходить через точку О1 з кутовим коефіцієнтом
. Із рівняння прямої, яка проходить через точку О1 з кутовим коефіцієнтом  , отримаємо (x2-2)=
, отримаємо (x2-2)=  (x1-6). Знайдемо координати точки Е
(x1-6). Знайдемо координати точки Е
 х1-3х2=0
х1-3х2=0
3 x1+x2 =15.
Вирішивши систему, отримаємо Е(4.5; 1.5).
L (E) = (4.5-6)2+ (1.5-2)2=2.5.
Відповідь: Мінімум дорівнює 2.5 досягається в точці (4.5; 1.5), максимум дорівнює 40 в точці (0;4).
3. Знайти екстремуми функції L=(x1-1)2+(x2-3)2 при обмеженнях  ,
,  .
.
 Вирішення
Вирішення
Область допустимого вирішення є частина кола з центром на початку координат з радіусом 5, яка розташована в I чверті. Лінії рівня – це окружності з центром в точці О1 і радіусі С, оскільки (x1-1)2+(x2-3)2=С. Точка О1 – це розроблена лінія рівня, яка відповідає мінімальному значенню С=0. глобальний максимум досягається в точці А, яка знаходиться на веретену області допустимого вирішення з лінією рівня найбільшого радіусу. При цьому L(A)=(5-1)2+(0-3)2=25.
Відповідь: Мінімум, дорівнює 0, досягається в точці (1;3), максимум, дорівнює 25, - в точці А(5;0).
4. Підприємець вирішив виділити на розширення своєї справи 150 тис. грн. Відомо, якщо на придбання нового устаткування затрачувати х тис. грн., а на зарплату прийнятих працівників у тис. грн., то приріст обсягу продукції складе Q=0.001x0.6·y0.4. Як необхідно розподілити виділені грошові ресурси, щоб приріст обсягу продукції був максимальним.
Вирішення
Цільова функція має вид 0.001x0.6·y0.4 →max при обмеженнях
 x+y≤150,
x+y≤150,
 .
.
Область допустимого вирішення – трикутник. Лінії рівня будуть мати вид 0.001x0.6·y0.4 =С. Виразивши у, отримуємо у=  . Оскільки максимум досягається в точці дотику лінії рівня з областю допустимого вирішення, то умова дотику має вигляд
. Оскільки максимум досягається в точці дотику лінії рівня з областю допустимого вирішення, то умова дотику має вигляд  =-1. Знайдемо похідну, отримаємо
=-1. Знайдемо похідну, отримаємо  =-1. Виразивши х, отримаємо х=
=-1. Виразивши х, отримаємо х=  . у=
. у=  =
=  .
.
Відповідь: Фактори х і у необхідно розподілити у відношенні 2:3.
Сутність методу Лагранжа складається в побудові функції L(x1,x2, …,хn)= f(x1,x2, …,хn)+  gi(x1,x2, …,хn), де
gi(x1,x2, …,хn), де 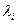 невідомі постійні, і знаходженні екстремуму функції L.
невідомі постійні, і знаходженні екстремуму функції L.
Має сенс наступна теорія: якщо точка (  ) є точкою умовного екстремуму функції f(x1,x2, …,хn) за умови g(x1,x2, …,хn)=0, то існують значення
) є точкою умовного екстремуму функції f(x1,x2, …,хn) за умови g(x1,x2, …,хn)=0, то існують значення 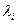 такі, що точка (
такі, що точка (  ) є точкою екстремуму функції L(
) є точкою екстремуму функції L(  ).
).
Розглянемо метод Лагранжа для функції двох змінних.
L(x1,x2,  )= f(x1,x2)+
)= f(x1,x2)+  g(x1,x2)
g(x1,x2)
Таким чином, для знаходження умовного екстремуму функції f(x1,x2) за умови g(x1,x2)=0 необхідно знайти вирішення системи
 L
L  =f
=f  (x1,x2)+
(x1,x2)+  g
g  (x1,x2)=0, (6.3)
(x1,x2)=0, (6.3)
L  =f
=f  (x1, x2) +
(x1, x2) +  g
g  (x1, x2) =0,
(x1, x2) =0,
L  = g(x1, x2) =0.
= g(x1, x2) =0.
Якщо і додаткові умови, при виконанні яких вирішення (x1,x2,  ) системи (6.3) визначає точку, в якій функція f досягає екстремуму, для цього потрібно розрахувати значення
) системи (6.3) визначає точку, в якій функція f досягає екстремуму, для цього потрібно розрахувати значення  і скласти визначник
і скласти визначник
 =-
=-  .
.
Якщо  <0, то функція має в точці (
<0, то функція має в точці (  ) умовний максимум, якщо
) умовний максимум, якщо  >0 – то умовний мінімум.
>0 – то умовний мінімум.
Вирішимо задачу методом множинника Лагранжа.
Загальні витрати виробництва задані функцією Т=0,5х2+0,6ху+0,4у2+ +700х+600у+2000, де х і у відповідно кількість товарів А і В. Загальна кількість виробленої продукції повинна дорівнювати 500 одиниць. Скільки одиниць товару А і В потрібно виробити, щоб витрати на їх виготовлення були мінімальними?
Вирішення
Складемо функцію Лагранжа
L(x, y,  ) =0,5х2+0,6ху+0,4у2+ +700х+600у+2000+
) =0,5х2+0,6ху+0,4у2+ +700х+600у+2000+  (х+у-500).
(х+у-500).
Дорівнюючи до нулю її часні похідні, отримаємо
 х+0,6у+700+
х+0,6у+700+  =0,
=0,
0,6х+0,8у+600+  =0,
=0,
х+у-500=0.
Вирішивши систему знайдемо (0, 500, -1000).
Використаємо достатні умови для визначення знайденого значення
L  (x0,y0)=1, L
(x0,y0)=1, L  (x0,y0)=0.8, L
(x0,y0)=0.8, L  (x0,y0)=0.6. Функція g= х+у-500. g
(x0,y0)=0.6. Функція g= х+у-500. g  =1, g
=1, g  =1.
=1.
 =-(0·L
=-(0·L  ·L
·L  + g
+ g  ·L
·L  · g
· g  + g
+ g  ·g
·g  ·L
·L  - g
- g  ·L
·L  ·g
·g  -0·L
-0·L  ·L
·L  - g
- g  · g
· g  ·L
·L  )=0,6>0
)=0,6>0
Таким чином, в точці (0;500) функція L має умовний мінімум.
Відповідь: Вигідно виробляти тільки 500 одиниці товару В, а товар А не виробляти.
Питання і завдання для самоконтролю до змістового модулю 3
Питання для самоконтролю:
1. Охарактеризуйте сутність цілочислового програмування.
2. Розкрийте напрями формулювання і вирішення задач цілочислового програмування:
3. Які методи використовуються при вирішенні задач цілочислового лінійного програмування. Охарактеризуйте їх.
4. Представте алгоритм вирішення задач цілочислового програмування.
5. В чому полягає метод Гомори і представте алгоритм вирішення задач цілочислового програмування цим методом.
6. В чому полягає метод віток і меж і представте алгоритм вирішення задач цілочислового програмування цим методом.
7. Охарактеризуйте математичну модель цілочислової транспортної задачі.
8. Назвіть види і висвітіть особливості вирішення задач цілочислового лінійного програмування.
9. Назвіть і охарактеризуйте основні поняття, які пов’язані з нелінійними зв’язками в економічних системах.
10. Визначте поняття нелінійного програмування й сутність вирішення задач нелінійного програмування.
11. Охарактеризуйте графічний метод вирішення задач нелінійного програмування при формуванні нелінійних оптимізаційних моделей.
12. Охарактеризуйте метод Лагранжа вирішення задач нелінійного програмування при формуванні нелінійних оптимізаційних моделей.
Завдання для самоконтролю:
1. Знайти оптимальний цілочисловий план задачі Z(X) = х1 - Зх2 + 5х3 + 2х4 –max за умови:
x1+x2+x3 =15
2x1+ 3x3+x4=8,
хj, > 0, хj — цілі числа, j = 1, 2, 3, 4.
2. Отримати цілочисловий оптимальний план задачі Z(X) x1— 4х2 — 2х3 + Зх4 —> max за умови
3x1+x2+8x3+x4=35
x1+x3+x4≤6
xj≥ 0, хj — цілі числа, j = 1, 2, 3, 4.
3. Контейнер обсягом 5 м3 розташований на контейнеровоз вантажністю 12 т. Контейнер необхідно заповнити вантажем двох найменувань. Маса одиниці вантажу mj (в тонах), обсяг одиниці вантажу Vj (в м3), вартості Cj (в умовних грошових одиницях) наведені в табл. 6.1.
Таблиця 6.1 - Маса одиниці вантажу mj (в тонах), обсяг одиниці вантажу Vj (в м3), вартості Cj (в умовних грошових одиницях)
| Вид вантажу у | mj | V, | Сj |
Необхідно завантажити контейнер таким чином, щоб вартість ватажу, шо перевозиться була максимальною.
4. Знайти екстремуми функції L(x1,x2)=2x1+x2 при обмеженнях 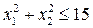 ,
,  .
.
5. Підприємець вирішив виділити на розширення своєї справи 50 тис. грн. Відомо, якщо на придбання нового устаткування затрачувати х тис. грн., а на зарплату прийнятих працівників у тис. грн., то приріст обсягу продукції складе Q=0.001x0.4·y0.2. Як необхідно розподілити виділені грошові ресурси, щоб приріст обсягу продукції був максимальним.
6. Загальні витрати виробництва задані функцією Т=0,8х2+0,7ху+0,6у2+800х+500у+1600, де х і у відповідно кількість товарів А і В. Загальна кількість виробленої продукції повинна дорівнювати 400 одиниць. Скільки одиниць товару А і В потрібно виробити, щоб витрати на їх виготовлення були мінімальними?
Читайте також:
- Active-HDL як сучасна система автоматизованого проектування ВІС.
- B. Тип, структура, зміст уроку і методика його проведення.
- BANKING SYSTEM. Банковская система
- D – моделювання в графічній системі КОМПАС
- D. СОЦИОИДЕОЛОГИЧЕСКАЯ СИСТЕМА ВЕЩЕЙ И ПОТРЕБЛЕНИЯ
- Demo 11: Access Methods (методи доступу)
- Demo 7: Модель OSI (модель взаімодії відкритих систем)
- H) інноваційний менеджмент – це сукупність організаційно-економічних методів управління всіма стадіями інноваційного процесу.
- I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
- I. Органи і системи, що забезпечують функцію виділення
- I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
- II. Анатомічний склад лімфатичної системи
| <== попередня сторінка | | | наступна сторінка ==> |
| Сутність нелінійних зв’язків в економічних системах | | | Змістовий модуль 4 |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |