
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Моделювання найпростішого потоку.
Для найпростішого потоку викликів з параметром 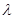 проміжки
проміжки 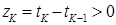 часу між послідовними викликами потоку розподілені за експоненціальним законом з тим же параметром
часу між послідовними викликами потоку розподілені за експоненціальним законом з тим же параметром 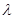 :
:

Ця обставина дозволяє сформувати процес надходження викликів найпростішого потоку на заданому інтервалі часу за допомогою метода Монте-Карло, який базується на наступній теоремі:
Теорема: Якщо ri - випадкові числа, рівномірно розподілені на (0, 1), то можливе значення xi безперервної випадкової величини Х із заданою функцією розподілу F(х), що відповідає ri є коренем рівняння F(xi) = ri .
Згідно з цією теоремою, для отримання послідовності випадкових значений zk, розподілених за експоненціальним законом з параметром 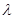 , потрібно для кожного випадкового числа ri(0, 1), що генерується на ПЕОМ датчиком псевдовипадкових чисел, вирішити рівняння
, потрібно для кожного випадкового числа ri(0, 1), що генерується на ПЕОМ датчиком псевдовипадкових чисел, вирішити рівняння
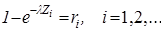
Вирішуючи це рівняння відносно 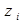 ,маємо:
,маємо:
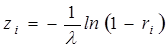
Оскільки випадкові числа ri належать інтервалу (0, 1), то і число 1 – ri також є випадковим (з тим же рівномірнім розподілом) з інтервалу (0,1). Тому для обчислення zi можна примінити простішу формулу:
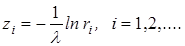 (1.11)
(1.11)
При цьому, якщо потік розглядається на інтервалі часу [T1, T2], то момент tk надходження викликів найпростішого потоку визначається співвідношенням
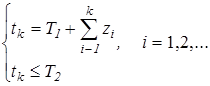 (1.12)
(1.12)
2. Порядок виконання роботи:
2.1. Згенерувати випадкові рівномірно розподілені числа від 0 до 1 (за допомогою будь якого генератора псевдо випадкових чисел).
2.2 За формулою (1.11) отримати zi для проміжків між викликами. Прийняти l = 10(N+1)/(N+4) (викл/хв); де N – номер по журналу.
2.3 На проміжку [T1, T2 ], T1 = N+1, T2 =N+36 хв. отримати послідовність tk моментів надходження викликів згідно з (1.12)
2.4 Отримані результати звести у таблицю
| ri | zi | tk |
| r1 | z1 | t1 |
| r2 | z2 | t2 |
| . | . | . |
| . | . | . |
2.5 Провести статистичну обробку отриманих результатів, для цього розділити заданий інтервал на 50 рівних проміжки довжиною:
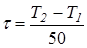 (хв);
(хв);
2.6 Для кожного проміжку визначити x(t) – кількість викликів, що потрапили в проміжок довжиною t
| N проміжку | . . . | |||
| x(t) |
2.7 Отримати таблицю статистичного розподілу випадкової величини
| x(t) | . . . | |||
| Nk | n1 | n2 | n3 | . . . |
n = å nk = 50
nk – кількість проміжків, в які потрапило к викликів.
2.8. Визначити модельне значення параметра потоку:
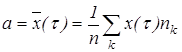 - мат. очікування числа викликів в проміжку.
- мат. очікування числа викликів в проміжку.
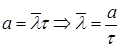
2.9. Порівняти задане (l) і модельне ( 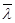 ) значення параметра потоку та організувати ітераційну процедуру обчислення останнього до досягнення точності 5 %.
) значення параметра потоку та організувати ітераційну процедуру обчислення останнього до досягнення точності 5 %.
2.10. Для отриманого ( 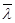 ) значення параметра потоку обчислити значення
) значення параметра потоку обчислити значення
1)Імовірність відсутності викликів P0 ( t ) за час t = N/15;
2)Імовірність надходження одного виклику P1 (N/10) ;
3)Імовірність надходження чотирьох викликів P4 (N/5);
4)Імовірність надходження не менш п’яти викликів за час N/3
P³5 ( )=1 - (P0 + P1 + P2 + P3 + P4 );
5) надходження менш трьох викликів за N/20
P<3 ( t )= P0 + P1 + P2 ;
6)Імовірність того, що проміжок між викликами zk
P[N/20< zk < N/10 ] = F(N/20) – F(N/10) .
Зробити висновки
3. Контрольні питання.
1. За якими властивостями класифікуються випадкові потоки ?
2. Дати визначення стаціонарності, ординарності, післядії.
3. Дати визначення числовим характеристикам випадкових потоків - параметра 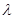 ; інтенсивності
; інтенсивності  ; провідної функції потоку.
; провідної функції потоку.
4. Для яких потоків співпадають значення параметра та інтенсивності?
5. За яким законом розподілено в найпростішому потоці
a. інтервал між сусідніми викликами?
b. кількість викликів, що потрапили в інтервал заданої довжини?
ЛАБОРАТОРНА РоБОТА №2
Об’єднання найпростіших потоків
Мета: Дослідити суму двох найпростіших потоків і перевірити відповідність результуючого потоку моделі найпростішого.
Читайте також:
- D моделювання ландшафтних комплексів
- D – моделювання в графічній системі КОМПАС
- Алгоритм моделювання систем масового обслуговування
- Аналiз ризику методами iмiтацiйного моделювання
- Аналіз ризику через моделювання.
- Бізнес-моделювання в системі управління розвитком підприємства. Поняття та етапи формування бізнес-моделі
- Виберіть відповідне визначення поняття: Моделювання – це
- Видаток і середня швидкість ламінарного потоку.
- Види моделювання та особливості їх використання
- Визначення економіко-математичного моделювання. Види моделей. Основні етапи моделювання
- Відображення і моделювання процесів
- ВІЛЬНИЙ ПОШУК (у тому числі ВАЛІДАЦІЯ) ® ПРОГНОСТИЧНЕ МОДЕЛЮВАННЯ ® АНАЛІЗ ВИКЛЮЧЕНЬ
| <== попередня сторінка | | | наступна сторінка ==> |
| Розподіл Пуассона | | | Теоретичні відомості |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |