• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Спеціальні методи імітації деяких дискретних розподілів

Загальний підхід імітації дискретно розподілених величин у деяких випадках може бути замінений спеціальними методами імітації, котрі ураховують специфічні особливості розподілів. Покажемо цю можливість для трьох розподілів.

Рівномірний дискретний розподіл має такий вигляд:

де k = 0, 1, 2,....

Для імітування цієї випадкової величини досить здійснити перетворення .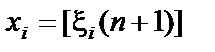

Геометричний розподіл імітується з допомогою перетворення

Справді, випадкова величина

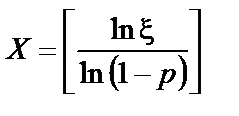
має геометричний розподіл. Це підтверджують такі міркування.

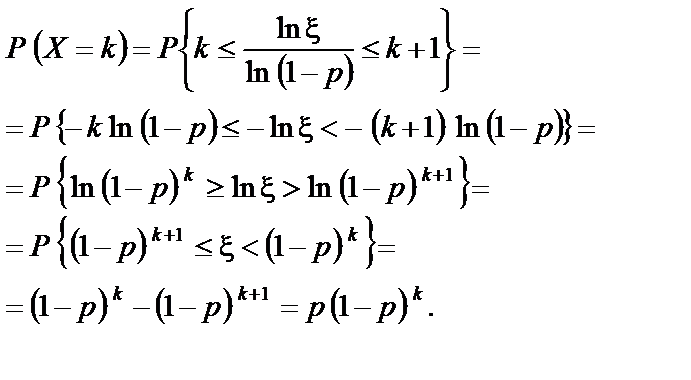
Цей метод імітації геометрично розподілених випадкових величин є найефективнішим.

Для імітації випадкових величин, що мають розподіл Пуассона, найчастіше застосовується метод Тотчера.

Цей метод грунтується на твердженні, що випадкова величина X, яка визначається відношенням

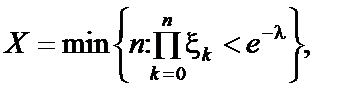
розподілена за законом Пуассона з параметром l.

Для генерування випадкової величини Х генеруємо 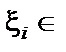РСП [0, 1] доти, доки не буде виконуватися нерівність

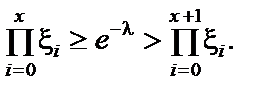
У більшості випадків для генерування розподілу Пуассона якраз і застосовується цей метод.

Питання для самоконтролю

1. З’ясуйте, коли виникає потреба в імітаційному моделюванні генерувати випадкові події.

2. Проаналізуйте стандартний метод імітації дискретної випадкової величини.

3. Для яких відомих вам дискретних розподілів має місце рекурентне співвідношення між ймовірностями сусідніх членів розподілу?

4. Поясніть перший і другий способи використання схеми випробувань за «жеребкуванням» для імітації незалежних і залежних подій.

5. Які переваги і які вади мають способи використання схеми випробувань за «жеребкуванням»?

6. Поясніть, чому і як використовуються несумісні у сукупності події в схемі випробувань за «жеребкуванням».

Тема 8

Читайте також:

1. B. Тип, структура, зміст уроку і методика його проведення.
2. Demo 11: Access Methods (методи доступу)
3. I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
4. II. МЕТОДИЧНІ ВКАЗІВКИ
5. II. УЧЕБНЫЕ И МЕТОДИЧЕСКИЕ ПОСОБИЯ, ПРАКТИКУМЫ
6. IV. КЕРІВНИЦТВО, КОНТРОЛЬ І НАДАННЯ ОРГАНІЗАЦІЙНО-МЕТОДИЧНОЇ ДОПОМОГИ ПРАКТИКАНТАМ.
7. IV. Учебно-методические рекомендации
8. IV. Электронное учебно-методическое обеспечение дисциплины.
9. V. ІНДИВІДУАЛЬНІ ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ ТА МЕТОДИЧНІ РЕКОМЕНДАЦІЇ ДО ЇХ ВИКОНАННЯ
10. V. Обов'язки методиста кафедри педагогіки
11. VIІ. Короткі методичні вказівки до роботи студентів на практичному занятті
12. А) Методика проведення заняття

Переглядів: 751