• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Інтерполяційний кубічний сплайн

Інтерполяційним кубічним сплайном, що відповідає функції f(x), визначеної у заданих вузлах, називають функцію s(x), що задовольняє такі умови:

1. На кожному інтервалі [Xe_i-1,Xe_i] i, i=1…Ne-1 функція s(x) є многочленом третього степеня.

2. Функція s(x), а також її перша і друга похідні є неперервними на інтервалі[al, bl].

3. У вузлах інтерполювання вона збігається із функцією f(x): s(Xe_i )=f(Xe_i ), i=0…Ne-1. Останню умову називають умовою інтерполювання.

Розглянемо один із можливих способів побудови інтерполяційного кубічного сплайна s(x). З цією метою на кожному з інтервалів [Xe_i-1,Xe_i], i =1…Ne-1 функцію s(x)=s_i(x) шукатимемо у вигляді многочлена третього степеня:

(1)

, i=1…N_e

де а_і b_i c_i d_i - коефіцієнти, що підлягають визначенню. З’ясуємо зміст уведених коефіцієнтів.

Маємо:

Тому a_i=s_i(Xe_i) b_i=s_i^’(Xe_i) c_i= s_i^’’(Xe_i) d_i= s_i^’’’(Xe_i).

Оскільки інтерполянта, за означенням, збігається з вузлами інтерполювання (тобто s_i(Xe_i)= f(Xe_i) i=1…Ne-1 одержимо: a_i=f(Xe_i) i=1…Ne-1. Довизначимо, окрім того, a₀=f(Xe₀).

Вимога неперервності функції s(x) спричинює до умов s_i(Xe_i)= s_i(Xe_i+1) i=1…Ne-2.

Звідси, з огляду на вирази для функцій s_i(x), одержуємо, при i=1…Ne-2, рівняння:

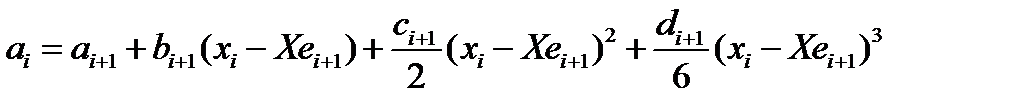
Позначаючи h_i=Xe_i - Xe_i-1 перепишемо ці рівняння так:

, i=1…Ne-1 (2)

Умови неперервності першої похідної s_i^’(Xe_i)= s_i+1^’(Xe_i), i=1…Ne-2, спричинюють до рівнянь:

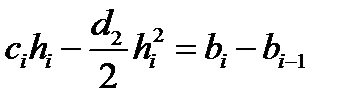i=1…Ne-1. (3)

З умов неперервності другої похідної одержуємо рівняння:

i=1…Ne-1. (4)

Об’єднуючи рівняння (2)–(4), одержимо систему із 3*Ne-3 рівнянь відносно 3*(Ne-1) невідомих, b_i c_i d_i i=1…Ne-1.

Два відсутніх рівняння можна одержати, задаючи ті чи інші граничні умови для s(x) . Припустимо, наприклад, що функція f(x) задовольняє умовам f^’’’(al)=f^’’’(bl)=0. Тоді природно вимагати, щоб s^’’(al)=s^’’(bl)=0. Звідси одержуємо: s^’’(Xe₀)=, s_Ne-1(Xe_Ne-1)=0, тобто c₁-d₁h₁=0 c_n=0.

3.4 Рівняння для визначення коефіцієнтів кубічного сплайна

Зауважимо, що умова c₁-d₁h₁=0 збігається з рівнянням (4) при1, i=1 якщо c₀=0. Отож, ми отримали замкнуту систему рівнянь для визначення коефіцієнтів кубічного сплайна:

i=1…Ne-1 c₀=c_Ne-1=0 (5)

i=2…Ne-1 (6)

i=1…Ne-1 (7)

Переконаємось у тому, що ця система має єдиний розв’язок. Вилучимо з цих рівнянь змінні b_i d_i i=1…Ne-2. Одержимо систему, що містить тільки c_i i=1…Ne-2. Щодо цього розглянемо два сусідніх рівняння:

Віднімаючи від першого рівняння друге, одержимо:

Підставляючи знайдений вираз для b_i-bi_-1 у праву частину рівняння(7.7.6), одержимо:

(8)

Далі, з рівняння (5) одержуємо:

Підставляючи ці вирази у (8), приходимо до рівняння:

Остаточно, для визначення коефіцієнтів c_i , одержуємо систему рівнянь:

(9)

i=1…Ne-2 c₀=c_Ne-1=0

Внаслідок діагональної переваги система (9) має єдиний розв’язок. Системи із тридіагональною матрицею коефіцієнтів, на практиці розв’язують методом, який є значно оптимальнішим за метод Гауса. Його називають методом прогонки. За знайденими коефіцієнтами c_i коефіцієнти d_i і b_i визначають за явними формулами:

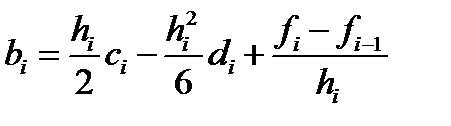i=1…Ne-1 (10)

Отож, доведено існування єдиного кубічного сплайна, що відповідає умовам 1–3 і граничним умовам s^’’(al)=s^’’(bl)=0 .

Блок-схему алгоритму обчислення коефіцієнтів кубічного сплайна, згідно із теорією, яку наведено вище, зображено на рис.1. Ідентифікатором Ma позначено матрицю коефіцієнтів системи лінійних алгебричних рівнянь (11), з якої знаходять невідомі коефіцієнти c_i i=1…Ne-1 Вона є тридіагональною. Її структуру подаємо нижче:

=

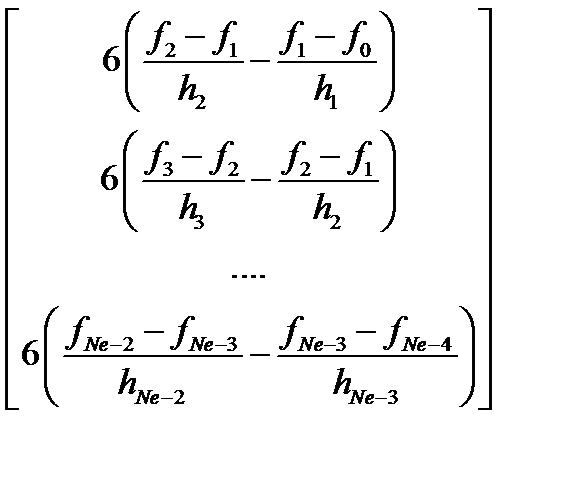(11)

Читайте також:

1. Блок-схема табулювання кубічного сплайну
2. Лекция №8. Кусочно-линейная интерполяция. Сплайн-интерполяция.
3. Сплайн (Spline)
4. Сплайн (Spline)
5. Сплайни.

Переглядів: 1867