• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Координати центру ваги складних фігур.

1) Центр тяжіння дуги кола. Розглянемо дугу АВ радіусу R з центральним кутом . В силу сімметрії центр тяжіння цієї дуги лежить на осі Ox

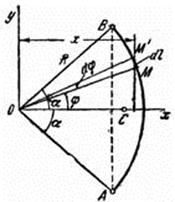
Знайдемо координату Хс по формулі .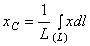

Для цього виділимо на дузі АВ елемент ММ' завдовжки , положення якого визначається кутом 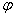. Координата х елементу ММ' буде . Підставляючи ці значення х і 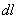і маючи на увазі, що інтеграл має бути поширений на всю довжину дуги, отримаємо:

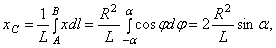
где L - длина дуги АВ, равная . Отсюда окончательно нахо­дим, что центр тяжести дуги окружности лежит на ее оси симметрии на расстоянии от центра О, равном

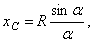
де кут 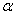вимірюється в радіанах.

2) Центр тяжіння площі трикутника. Розіб'ємо площу трикутника

ABD прямими, паралельними AD, на вузькі смужки; центри тяжіння цих смужок лежатимуть на медіані BE трикутника.

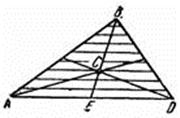
Отже, і центр тяжіння усього трикутника лежить на цій медіані.

Аналогічний результат виходить для двох інших медіан. Звідси робимо висновок, що центр тяжіння площі трикутника лежить в точці перетину його медіан.
При цьому, як відомо

3) Центр тяжіння площі кругового сектора. Розглянемо круговий

сектор ОАВ радіусу R з центральним кутом. Розіб'ємо подумки площу сектора ОАВ радіусами, проведеними з центру О, на п секторів. У межі, при необмеженому збільшенні числа, ці сектори можна розглядати як плоскі трикутники, центри тяжіння яких лежать на дузі DE радіусу . Отже, центр тяжіння сектора ОAB буде зівпадати з центром тяжіння дуги DE. Остаточно отримаємо, що центр тяжіння площі кругового сектора лежить на його центральній осі симетрії на відстані від початкового центру О, дорівнює

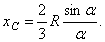
Читайте також:

1. Аксіоматика структурних і складних типів даних. Структурні типи даних.
2. Аналіз результатів практичної діяльності Київського освітньо-методичного центру соціальної роботи
3. БУДОВА АКТИВНОГО ЦЕНТРУ АНТИТІЛ
4. Будова активного центру ферментів
5. Важливим параметром конденсаторів є пробивна напруга конденсатора. Чим вона більша, тим надійніший конденсатор, тим більша енергія може сконцентруватись на ньому.
6. Вантажообіг і координати магазинів, які обслуговуються
7. Вектори. Лінійні дії над векторами. Властивості. Довжина вектора. Кут між векторами. Відстань між 2-ма точками. Проекція вектора на вісь. Координати вектора.
8. Виведення формул для знаходження площі паралелограма, трикутника, трапеції. Формули для знаходження площ поверхонь просторових геометричних фігур.
9. Визначення DРф на відстані L від центру вибуху
10. Визначення координат центру паралельних сил.
11. Визначення скалярного добутку через координати.
12. Визначення центру обертання провідної ланки або другий наслідок основної теореми зачеплення.

Переглядів: 1955