• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Вектори. Лінійні дії над векторами. Властивості. Довжина вектора. Кут між векторами. Відстань між 2-ма точками. Проекція вектора на вісь. Координати вектора.

Геометричний вектор-це напрямлений відрізок прямої. Довжина вектора – відстань відстань від початку до кінця вектора. Вектор, довжина якого=1 називається одиничним. Вектор, довжина якого=0 називають нульовим вектором. Два вектори називаються рівними, якщо рівні їх довжини, вони паралельні і напрямлені в одну сторону. Вектори називаються колінеарними, якщо вони лежать на одній або паралельних прямих. Вектори наз. компланарними, якщо вони в одній площині, або паралельних площинах. Під лінійними операціями над векторами розглядають додавання, віднімання і множення вектора на число. Якщо вектор 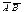заданий двома точками, то тоді координати 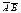= від координат кінця віднімаємо координати початку. Координатами вектора називають його проекцію на координатну вісь. Проекцію на вісь L називають число, яке = довжині вектора 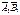, взяте із знаком «+», або -, в залежності від того, як напр. вектор 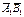, в ту, чи протилежну сторону осі L.

Властивості:

1)

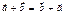
2)

3)

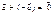
4)

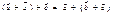
5)

6)

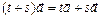
7)

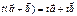
13.Лінійний векторний простір.Лінійно-залежні і лінійно-незалежні системи векторів. Базис простору. Розкладання вектора за базисом.N-вимірний вектор

Сукупність векторів у просторі, після введення в неї операцій додавання і множення на число називається трьохвимірним векторним простором і позначається . Аналізуя сукупність векторів на площині , назвемо лінійним векторним простором . На прямій – одновимірним лінійним простором 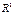. Простір 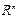, завжди містить нульовий вектор. Простір , завжди замкнутий відносно операцій додавання і множення вектора на число. Лінійною комбінацією векторів 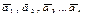називається вираз виду , де - деякі числа. Тобто під лінійною комбінацією векторів розуміюь новий вектор, який одержуємо в результаті лінійних операцій над векторами. Система векторів називається лінійно незалежною, якщо рівність

виконується лише за умови

.

Якщо рівність (2.1) можлива хоча б при одному із чисел , то система векторів називається лінійно залежною.

Можна сформулювати еквівалентне означення:

система векторів 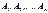називається лінійно залежною, якщо хоча б один із векторів системи є лінійною комбінацією решти векторів системи. Наприклад:

.

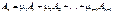Якщо якась підсистема системи векторів лінійно залежна, то і вся система лінійно залежна. Якщо система векторів лінійно незалежна, то і довільна її підсистема теж лінійно незалежна.

Розглянемо лінійно залежну систему векторів 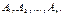Візьмемо таку лінійно незалежну підсистему 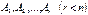, до якої не можна додати жодного вектора, щоб не порушити лінійну незалежність. Таку систему називають максимальною лінійно незалежною підсистемою даної системи векторів.

Кількість векторів, які входять в довільну максимально лінійно незалежну підсистему векторів, називають рангом системи векторів.

Розглянемо систему векторів

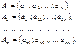
Ранг системи векторів дорівнює рангу матриці, яка утворена координатами векторів цієї системи, тобто рангу матриці

.

Таким чином, якщо система векторів лінійно-залежна, то один з цих векторів можна представити у вигляді лінійної комбінації решти векторів. Нехай лінійна комбінація векторів=0. Припустимо, що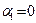

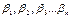Числа називаються коефіцієнтами розкладу, найчастіше використовується розклад за базисом. Базисом n-вимірного простору називається сукупність n-лінійно-незалежних векторів цього простору. Базисом на прямій є любий ненульовий вектор, що лежить на цій прямій. Базисом на площині наз. два любих неколініарних вектори. Базисом у просторі називаються три компланарні вектори. Нульовий простір базису не має, так як не містить лінійно-незалежних векторів. Нескінченно - вимірний простір, в якому число базисних векторів невизначено, також не має базису. Мають місце наступні твердження:

1) Любі два неколініарні вектори утворюють базис

2) Трикомпланарні вектори завжди лінійно-залежні. Упорядкована система 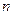дійсних чисел

називається 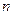-вимірним вектором.

Числа називаються координатами вектора.

Читайте також:

1. V Ідентифікація, раціоналізація, проекція, інтроекція, агресія, зворотна реакція та їх комплекси.
2. А) Товар і його властивості.
3. Алкани, їх хімічні властивості.
4. Аналізатори людини та їхні властивості.
5. Аналізатори людини та їхні властивості.
6. Багатоконтурні лінійні електричні ланцюги
7. Базис. Розклад вектора по даному базису
8. Білінійні і квадратичні форми в евклідовому просторі
9. Будова атомів та хімічний зв’язок між атомами визначають будову сполук, а отже і їх фізичні та хімічні властивості.
10. В положение ее в данной момент времени (приращение радиуса-вектора точки за рассматриваемый промежуток времени), называется переменками.
11. Вантажів: чоловікам – масою не більше 50 кг на відстань, що не пере1
12. Вантажообіг і координати магазинів, які обслуговуються

Переглядів: 1835