• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Максимальні значення коефіцієнта довіри

Схема відбору	для	для р
Повторна
Безповторна

6. Аналіз взаємозалежності між точністю, надійністю та обсягом вибірки

Існує певна взаємозалежність між обсягом вибірки п та точністю δ і надійністю γ інтервальної оцінки будь-якого параметра генеральної сукупності незалежно від схеми відбору. Проаналізуємо цю залежність на прикладі інтервального оцінювання генеральної середньої для повторної вибірки:

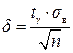(2.7)

Оскільки інтегральна функція Лапласа Ф(х) є зростаючою, то із рівності витікає, що із збільшенням надійності γ збільшується значення довірчого числа t_γ. Це, в свою чергу, призводить до збільшення граничної помилки δ (див. (2.7), тобто зменшення точності оцінки при фіксованому п. Навпаки, збільшення точності оцінки (тобто зменшення δ) неминуче тягне за собою зменшення її надійності γ.

Існує єдина можливість збільшувати надійність без зменшення точності, або збільшувати точність без зменшення надійності, або одночас­но збільшувати точність і надійність – це збільшення обсягу вибірки п.

Приклад постановки і розв’язування типової задачі.

Постановка задачі.

За даними 10%-ої вибірки 20,0; 24,1; 15,1; 25,0; 22,3; 26,3; 16,2; 23,2; 24,5; 10,2; 36,1; 21,6; 27,8; 16,6; 7,8; 24,7; 35,0; 29,7; 17,3; 23,8; 26,3; 31,3; 20,7; 28,8; 31,5; 22,5; 16,8; 6,7; 23,1; 27,4; 12,5; 24,4; 26,2; 17,9; 33,5; 20,8; 25,2; 20,7; 17,7; 21,0; 26,7; 18,8; 22,9; 34,0; 27,5; 30,2; 23,4; 13,7; 11,4; 20,5; 24,2; 28,1; 18,4; 19,5; 24,6; 27,0; 37,6; 23,8; 28,9; 32,4; 22,3; 15,5; 28,5; 18,4; 21,5; 26,8; 9,2; 15,9; 20,1; 27,4; 24,3; 14,1; 20,6; 39,8; 19,1; 29,1; 21,7; 28,7; 14,8; 22,3; 30,6; 24,1; 29,6; 23,6; 29,3; 25,6; 19,0; 24,0; 25,4; 34,8; 20,3; 5,1; 21,0; 33,9; 24,7; 19,5; 22,8; 25,4; 32,5; 24,0 з нормально розподіленої генеральної сукупності X:

1. З надійністю γ = 95 % знайти надійний інтервал для генеральної середньої та генеральної частки р значень ознаки Х, менших за .

2. Знайти мінімально необхідні обсяги вибірок п, які з надійністю γ = 95 % забезпечать граничні помилки δ_х = для оцінки генеральної середньої та δ_w= для генеральної частки р, розглядаючи дослідження, проведені в л. р. № 1, як пробні для наближеного обчислення та w.

3. Знайти надійності γ, з якими заданий надійний інтервал
( – 0,05 * ; + 0,05 * ) накриває генеральну середню , а надійний інтервал (w– 0,15 * w; w+ 0,15 * w) – генеральну частку р.

Всі обчислення провести для повторної і безповторної схем відбору.

4. Зробити висновки.

Розв’язування задачі

1. Оскільки обсяг вибірки п=100>30, то надійні інтервали для генеральних середньої та частки р будемо знаходити за формулами: для повторної вибірки – відповідно (2.1) і (2.3), для безповторної вибірки – відповідно (2.4) і (2.6). Оскільки у вибірку обсягом п=100 відібрано 10 % елементів генеральної сукупності, то обсяг останньої =1000. За таблицями інтегральної функції Лапласа (див. додаток 5) із умови Ф(t_γ )=γ/2 знаходимо t_0,95 =1,96. За результатами виконання л. р. № 1 =23,3; =6,58. За точкову оцінку генеральної частки р значень Х, менших за , візьмемо вибіркову частку w варіант, менших за :

,

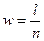де l – число варіант, менших за . Для нашого прикладу l = 47 і, відповідно, w=0,470. Тоді:

– – для повторної вибірки:

або (22,0; 24,6);

або (0,372; 0,568).

– – для безповторної вибірки:

або (22,1; 24,5);

або (0,377; 0,563).

2. Мінімально необхідні обсяги вибірок будемо знаходимемо за формулами, наведеними в таблиці 2.2. За умовою задачі задані граничні помилки інтервальних оцінок повинні становити: для середньої –

δ_х=0,1· =2,33; для частки – δ_w=0,2· w=0,094. Тоді:

– для повторної вибірки:

; .

– для безповторної вибірки:

; .

3. Для знаходження шуканих надійних імовірностей γ спочатку обчислимо максимальні значення відповідних коефіцієнтів довіри t за формулами, наведеними в таблиці 2.3. За умовою задачі граничні помилки інтервальних оцінок повинні становити: для середньої – δ_х=0,05 · =1,165; для частки – δ_w=0,15 ·w=0,0705. Тоді:

– для повторної вибірки:

, γ=2 · Ф(1,77)=0,9232;

, γ=2 · Ф(1,41)=0,8414.

– для безповторної вибірки:

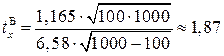, γ=2 · Ф(1,87)=0,9386;

; γ=2 · Ф(1,49)=0,8638.

4. За результатами проведених досліджень можна зробити такі висновки.

При здійсненні вибірки за повторною схемою:

а) генеральні середня і частка р з надійністю 95 % повинні накриватись інтервалами відповідно (22,0; 24,6) та (0,372; 0,568);

б) мінімально необхідні обсяги вибірок для того, щоб з надійною імовірністю 0,95 генеральна середня була накрита інтервалом
(23,3–2,33; 23,3+2,33) або (20,1; 25,6), а генеральна частка р – інтервалом (0,47–0,094; 0,47+0,094) або (0,376; 0,564) становлять відповідно 31 та 109;

в) маючи вибірку обсягом п=100, можна стверджувати, що задані надійні інтервали (23,3–1,165; 23,3+1,165) або (22,1; 24,5) та
(0,47–0,0705; 0,47+0,0705) або (0,400; 0,541) повинні накривати відповідно генеральні середню та частку р з надійністю відповідно ≈92 % та ≈84 %.

При здійсненні вибірки за безповторною схемою:

а) генеральні середня і частка р з надійністю 95 % повинні накриватись інтервалами відповідно (22,1; 24,5) та (0,377; 0,563);

б) мінімально необхідні обсяги вибірок для того, щоб з надійною імовірністю 0,95 генеральна середня була накрита інтервалом
(23,3–2,33; 23,3+2,33) або (20,1; 25,6), а генеральна частка р – інтервалом (0,47–0,094; 0,47+0,094) або (0,376; 0,564) становлять відповідно 30 та 98;

в) маючи вибірку обсягом п=100, можна стверджувати, що задані надійні інтервали (23,3–1,165; 23,3+1,165) або (22,1; 24,5) та
(0,47–0,0705; 0,47+0,0705) або (0,400; 0,541) повинні накривати відповідно генеральні середню та частку р з надійністю відповідно ≈94 % та ≈86 %.

Контрольні запитання.

1. Дати визначення: суцільного, несуцільного та вибіркового спостережень; генеральної та вибіркової сукупності; точкової та інтервальної оцінок параметра генеральної сукупності; помилки репрезентативності, систематичної та випадкової помилки; репрезентативної вибірки; надійної ймовірності; граничної та стандартної помилки; коефіцієнта довіри.

2. Назвати два основні фактори, що забезпечують репрезентативність вибірки.

3. Дати визначення: основних схем відбору – повторного і безповторного; основних способів відбору – простого випадкового, механічного, типового, серійного.

4. Вказати, в яких випадках доцільно застосовувати певні схеми та способи відбору.

5. Пояснити від чого залежать та як вибираються значення коефіцієнта довіри.

6. Записати формули для обчислення: середніх помилок інтервальних оцінок (табл. 2.1); мінімально необхідного обсягу вибірки (табл. 2.2); максимальних значень коефіцієнта довіри (табл. 2.3) та пояснити зміст позначень.

7. Пояснити взаємозалежність між обсягом вибірки, точністю і надійністю інтервальних оцінок.

Читайте також:

1. A) Оцінка захисних споруд за ємністю – визначення коефіцієнта Квм.
2. CMM. Визначення моделі зрілості.
3. DIMCLRE (РЗМЦВЛ) - колір виносних ліній (номер кольору). Може приймати значенняBYBLOCK (ПОБЛОКУ) і BYLAYER (ПОСЛОЮ).
4. I визначення впливу окремих факторів
5. II. Визначення мети запровадження конкретної ВЕЗ з ураху­ванням її виду.
6. II. Мотивація навчальної діяльності. Визначення теми і мети уроку
7. II. Фактори, що впливають на зарплату при зарубіжних призначеннях
8. ISO 15504. Призначення і структура стандарту
9. Iсторичне значення революції.
10. Ne і ne – поточне значення потужності і частоти обертання колінчастого вала.
11. Ocнoвнi визначення здоров'я
12. S Визначення оптимального темпу роботи з урахуванням динаміки наростання втоми.

Переглядів: 711