• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Прогнозування часових рядів за допомогою характеристик динаміки

У деяких найпростіших випадках для неперервного рівномірного ряду без коливань точковий прогноз можна зробити без аналітичного вирівнювання останнього за допомогою попередньо обчислених певних характеристик динаміки ряду:

1. Якщо всі абсолютні ланцюгові прирости 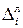рівні між собою (хоча б наближено), тобто рівні у_і часового ряду рівномірно зростають (коли 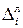>0) або спадають (коли 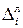<0), то кожний наступний рівень, починаючи з
(п+1)-го, можна знаходити, додаючи до попереднього середній абсолютний приріст : у_п+1=у_п+ . Очевидно, що в цьому випадку рівні ряду утворюють (хоча б наближено) арифметичну прогресію з різницею , що можна використовувати для виконання довгострокових прогнозів:

у_п+l =у_п+l · ( 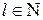). (4.29)

2. Якщо всі ланцюгові коефіцієнти зростання 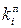рівні між собою (хоча б наближено), то кожний наступний рівень часового ряду, починаючи з
(п+1)-го, можна знаходити множенням попереднього на середній коефіцієнт зростання 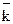: у_п+1=у_п· . Очевидно, що в цьому випадку рівні ряду утворюють (хоча б наближено) геометричну прогресію із знаменником , що можна використовувати для виконання довгострокових прогнозів:

у_п+l =у_п· 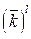( 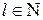). (4.30)

Слід підкреслити, що точкове прогнозування вищенаведеними наближеними способами слід вважати досить неточним, оскільки залежить від значення останнього рівня у_п часового ряду, яке може мати суттєво випадковий характер.

Читайте також:

1. I. Загальна характеристика політичної та правової думки античної Греції.
2. II. ВИРОБНИЧА ХАРАКТЕРИСТИКА ПРОФЕСІЇ
3. II. Морфофункціональна характеристика відділів головного мозку
4. IV. Определение метрологических характеристик контрольно - измерительных приборов при различных режимах эксплуатации
5. S Визначення оптимального темпу роботи з урахуванням динаміки наростання втоми.
6. V. Поняття та ознаки (характеристики) злочинності
7. V.3. Общая характеристика кадрового состава муниципальной службы в республике Коми на 2004 год.
8. VII. Нахождение общего решения методом характеристик
9. VІII. Основи молекулярної фізики і термодинаміки
10. Аварії на хімічно-небезпечних об’єктах та характеристика зон хімічного зараження.
11. Аварійне та довгострокове прогнозування хімічної обстановки
12. Автобіографія. Резюме. Характеристика. Рекомендаційний лист

Переглядів: 390