Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Агрегатні (узагальнюючі) індекси

Визначальними ознаками інформаційної бази індексного аналізу є ступінь агрегованості та статистична природа показника. За ступенем агрегованості інформації індекси поділяються на індивідуальні та зведені. Вони позначаються відповідно символами i та I.Індивідуальні індекси характеризують співвідношення рівнів показника окремих елементів сукупності, зведені — певної множини елементів. У структурованій сукупності зведений індекс може бути груповим (субіндексом) або загальним (тотальним). Наприклад, в ієрархії динамічних індексів промислового виробництва динаміку обсягів окремих видів продукції (чавун, електроенергія, верстати) характеризують індивідуальні індекси, окремих галузей промисловості (металургія, енергетика, машинобудування) — субіндекси, промисловості в цілому — загальний індекс.

Показник, динаміку чи співвідношення якого характеризує індекс, називають індексованою величиною, йому надається певний символ. Наприклад, індивідуальний індекс фізичного обсягу продукції позначають 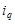, зведений індекс цін — 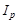. Символи p та q не випадкові, вони відповідають початковим літерам англійських слів price (ціна) та quantity (кількість).

Індивідуальний індекс — це відносна величина динаміки

або порівняння

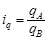Неодмінною умовою їх обчислення є порівнянність методики вимірювання чисельника та знаменника відношення, що являє собою індекс.

Щодо зведених індексів, то розрахунок кожного з них окремо передбачає вирішення низки методологічних питань. У підрозд. 9.2 розглядається методологія побудови зведених індексів цін і товарної маси, які вважаються спряженими.

9.2. Методологічні основи побудови зведених індексів

Зведений індекс показує, як у середньому змінився показник по сукупності елементів. Основою побудови зведених індексів є агрегування, узагальнення інформації. Нехай за даними про ціни на товари (j = 1, 2, 3, ...) за два періоди (t = 0,1) необхідно визначити зведений індекс цін:

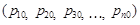та .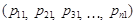

Агрегування інформації для зведеного індексу цін 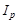можна здійснити трьома способами.

1. У вигляді відношення сум цін (індекс Дюто, 1735 р.):

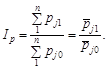
Поділивши чисельник і знаменник на n, цей індекс можна подати як відношення середніх цін.

2. Як середню арифметичну з індивідуальних індексів цін 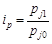(індекс Карлі, 1751 р.):

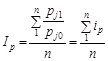3. Як середню геометричну з індивідуальних індексів (Джевон, 1863 р.):

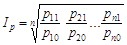Кожний з цих варіантів передбачає рівновагомість товарів у сукупності. Інакше зведений індекс неадекватно характеризуватиме сукупну зміну цін. Адже не можна визначити середню ціну, наприклад, 1 л вина та 1 кг хліба. Так само без урахування вагомості окремих товарів неможливо усереднити індивідуальні індекси цін: якщо ціни на хліб зросли на 10%, а на вино — удвічі, то це не означає, що в середньому ціни зросли на 55%.

Отже, при розрахунку зведеного індексу кожному j-му елементу необхідно надати певну «вагу», яка б ураховувала його відносну значущість. Очевидно, що ваги повинні мати однакову розмірність. Кількості товару q_j у натуральних одиницях вимірювання не можуть виконувати вагову функцію, а тому вагами є вартості товарів q_jp_j. Припустимо, що в базисному періоді вартості товарів становили q_j₀ p_j₀, тоді зважений індекс цін набирає вигляду

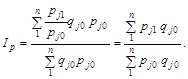
Це дві форми одного індексу — середньозважена та агрегатна. Основою середньозваженої форми є індекс Карлі, агрегатної — індекс Дюто.

Аналогічна ситуація виникає при агрегуванні фізичного обсягу продукції (товарної маси, кількості), якщо елементи сукупності не сумірні між собою, тобто не мають спільної міри:

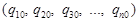та .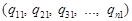

У такому разі їх агрегування можливе лише за умови зведення різнорідних елементів до одного порівнянного виду за допомогою певних сумірників. Найчастіше сумірниками є вартісні показники — ціна або собівартість одиниці продукції. Наприклад, при визначенні обсягів проданих на біржі товарів — металу, лісоматеріалів, цементу — сумірниками виступають ціни. Обсяги продажу записуються як 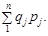Якщо за сумірник узяти собівартість с, агрегат інтерпретується як грошові витрати і набирає вигляду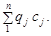

Іноді зручнішим є трудовий сумірник. Наприклад, при визначенні обсягів виконаних у сільському господарстві робіт (оранка, боронування, сівба тощо) як сумірник використовують трудомісткість, тобто затрати праці на одиницю виконаної роботи (позначимо t). Тоді загальний обсяг трудових затрат буде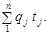

Зведений індекс фізичного обсягу 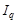також має дві форми — середньозважену та агрегатну:

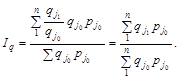
Як бачимо з формул наведених індексів 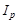та 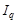, їх значення залежить від структури агрегату і динаміки окремих його елементів. Тому при визначенні зведеного індексу необхідно передусім обґрунтувати коло елементів, які підлягають агрегуванню в одне ціле. Наприклад, обґрунтовується споживчий кошик (набір споживчих товарів) при обчисленні індексу «вартості життя», перелік товарів і товарних груп при обчисленні індексу оптових цін тощо.

Підсумовування ведеться по всьому визначеному колу елементів як у чисельнику, так і в знаменнику, а тому надалі для простоти викладу навчального матеріалу у формулах зведених індексів ідентификаційні позначки елементів 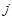не вказуються.

9.3. Агрегатна форма індексів

Агрегатний індекс — це співвідношення двох агрегатів, конкретних щодо змісту й часу. Агрегат є добутком спряжених величин. Одна з цих величин індексована — у чисельнику і знаменнику вона в різних періодах, інша є вагою чи сумірником індексованої величини і фіксується на одному й тому самому рівні.

Так, в індексі цін індексується ціна p, а кількість q являє собою вагу ціни і фіксується на одному й тому самому рівні; в індексі фізичного обсягу продукції індексується кількість q, а сумірник кількості — ціна p — фіксується:

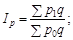
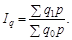
Ваги в індексі цін і сумірники в індексі фізичного обсягу можна фіксувати на рівні як базисного, так і поточного періоду. Для ілюстрації варіантів зважування використаємо матрицю агрегатів (рис. 9.1).

Рис. 9.1. Схема співвідношення агрегатів

На головній діагоналі матриці розміщено фактичні вартості товарів, на побічній — перехресні (умовні). По горизонталі розміщені агрегати з фіксованими вагами: у першому — на рівні базисного періоду, у другому — на рівні поточного. По вертикалі — агрегати з фіксованими сумірниками: у першому — на рівні базисного періоду, у другому — на рівні поточного. Порівняння агрегатів дає дві системи індексів — базисно-зважену (Ласпереса) та поточно-зважену (Пааше).

У базисно-зваженій системі перехресні агрегати побічної діагоналі порівнюються з базисним агрегатом головної діагоналі 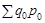, у поточно-зваженій системі агрегат головної діагоналі 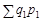порівнюється з перехресними агрегатами побічної діагоналі. Схематично системи зважування показано на рис. 9.1, а формули індексів наведені в табл. 9.1.

Таблиця 9.1

ФОРМУЛИ ІНДЕКСІВ ЦІН І ФІЗИЧНОГО ОБСЯГУ
ЗА РІЗНИХ СИСТЕМ ЗВАЖУВАННЯ

Базисно-зважена система (Ласпереса)	Поточно-зважена система (Пааше)

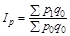
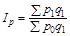
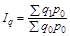
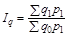
Обидві системи індексів рівноправні. Реальний економічний зміст мають не лише чисельник і знаменник індексу, а й різниця між ними. Вибір форми індексу залежить від мети дослідження та наявної інформації. Так, у зарубіжній статистиці індекс цін розраховується за Ласпересом, оскільки ґрунтується на даних про обсяги, отримані з переписів, вибіркових обстежень домогосподарств, інших джерел за минулий період. У вітчизняній статистиці при розрахунках індексів цін перевага надавалася формулі Пааше, оскільки визначальним показником була вартість поточного періоду. Індекс фізичного обсягу товарної маси, навпаки, обчислюється за формулою Ласпереса з фіксованими сумірниками на рівні базисного періоду. У такому разі динаміка цінового фактора не впливає на величину індексу. Зауважимо, що при незначній кореляції між цінами та товарною масою індекси, розраховані за Ласпересом і Пааше, практично однакові.

Розглянемо порядок розрахунку агрегатних індексів за даними про ціни та обсяги продажу через біржу агропродукції (табл. 9.2). У цьому прикладі агрегатами виступають фактичні за кожний місяць та умовні обсяги торгових оборотів біржи.

Таблиця 9.2

ДО РОЗРАХУНКУ АГРЕГАТНИХ ІНДЕКСІВ ЦІН І ФІЗИЧНОГО ОБСЯГУ

Продукція	Реалізовано, тис. т	Ціна за 1 т, грн.	Агрегати (торгові обороти, тис. грн.)
Серпень	Вересень	Серпень	Вересень	q₀p₀	q₁p₀	q₁p₁	q₀p₁
q₀	q₁	p₀	p₁
Борошно
Цукор
Олія
Разом	´	´	´	´

За даними таблиці зведені індекси цін 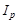та фізичного обсягу 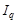, реалізованої через біржу агропродукції, становлять:

За Ласпересом:	За Пааше:

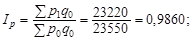
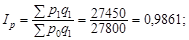
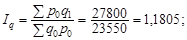
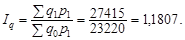
Тобто, біржові ціни на агропродукцію у вересні порівняно із серпнем зменшилися в середньому на 1,4%, реалізована товарна маса зросла в середньому на 18%.

Оскільки в структурі торгового обороту не відбулося значних змін, то розбіжності між індексами, обчисленими за різними системами зважування, неістотні. Будь-який з розрахованих індексів має певний ступінь умовності.

За наявності структурних зрушень у торгових оборотах використовують індекси із середніми вагами або усереднення різнозважених індексів за допомогою середньої геометричної, наприклад, індекс цін

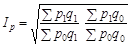Спираючись на формально-математичні критерії, яким відповідає усереднений індекс, І. Фішер назвав його «ідеальним», проте через відсутність конкретного економічного змісту цей індекс не набув широкого практичного застосування.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
	\|	Метод ланцюгових підставлень

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.007 сек.