• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Критичне значення

Межу малоймовірності Z називають рівнем істотності a. Очевидно, що a — це ймовірність ризику І, а тому залежно від змісту гіпотези Н₀ і наслідків її відхилення рівень істотності визначають у кожному конкретному дослідженні. Зазвичай вибирають один із рівнів a, для яких табульовані значення статистичних характеристик критеріїв. Це a = 0,10; 0,05; 0,025; 0,01.

Значення статистичної характеристики критерія Z_{1 – a} поділяє множину вибіркових значень Z на дві частини: а) область допустимих значень і б) критичну область. Якщо вибіркове значення Z потрапляє у критичну область, гіпотеза Н₀ відхиляється, якщо в область допустимих значень — не відхиляється. Саме тому значення Z_{1 – a} називають критичним.

Залежно від того, як сформульована альтернативна гіпотеза, критична область може бути односторонньою (ліво- чи правосторонньою) або двосторонньою (рис. 6.2).

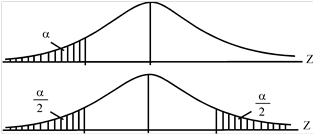
Рис. 6.2. Лівостороння та двостороння критичні області

Порядок перевірки статистичних гіпотез розглянемо на прик­ладі співвідношення середніх двох сукупностей. Припустимо, ведеться вибірковий контроль тривалості служби деталей одного виду, виготовлених за різними технологіями. Контролю піддано 5 деталей, виготовлених за старою технологією, і 4 — за новою, тобто n₁ = 5, n₂ = 4. Вибіркові оцінки середніх і дисперсій відповідно становили: = 580 год при 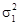= 308; = 612 год при 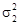= 329.

Різниця між середніми ( 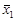– ) = (612 – 580) = 32 год.

Потрібно визначити, чи істотна ця різниця, тобто чи зумовлена вона відмінностями технологій, чи випадкова. Нульова гіпотеза формулюється на припущенні, що відхилення середніх випадкові Н₀: . Альтернативна гіпотеза передбачає, що нова технологія збільшує тривалість служби деталі: Н_а: 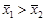. За такого формулювання Н_a виконується одностороння (правостороння) перевірка.

Статистичною характеристикою гіпотези Н₀: є нормоване відхилення середніх

,

яке підпорядковане розподілу Стьюдента з числом ступенів свободи k = n₁ + n₂ – 2.

У нашому прикладі k = 5 + 4 – 2 = 7; оцінка дисперсії розраховується як середня арифметична зважена з дисперсій, що характеризують варіацію тривалості служби деталей за кожною технологією

;

значення t-критерію

.

Перевіримо гіпотезу Н₀ проти Н_a з рівнем істотності a = 0,05. За даними табл. 6.3 критичне значення t_0,95 (7) = 1,89, що менше за фактичне (t = 2,37). Отже, нульова гіпотеза Н₀: відхиляється, і з імовірністю 0,95 можна стверджувати, що нова технологія збільшує термін служби деталей.

У разі двосторонньої перевірки гіпотези, коли Н_a: 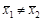, використовують критичне значення для , наприклад при a = 0,05 це буде t_0,975 (k).

Отже, статистична гіпотеза перевіряється в такій послідовності:

а) формулюють нульову Н₀ та альтернативну Н_a гіпотези;

б) вибирають статистичну характеристику Z, за значеннями якої перевіряють правильність гіпотези Н₀;

в) визначають рівень істотності a і відповідне йому критичне значення Z_{1 – a}; залежно від формулювання гіпотез Н₀ i Н_a критична область може бути одно- або двосторонньою;

г) за результатами вибірки розраховують фактичне (вибіркове) значення статистичної характеристики Z, яке порівнюють з критичним Z_{1 – a}; якщо Z > Z_{1 – a}, гіпотеза Н₀ відхиляється, при Z < Z_{1 – a} — не відхиляється.

Таблиця 6.3

ЗНАЧЕННЯ КВАНТИЛІВ t
РОЗПОДІЛУ СТЬЮДЕНТА ДЛЯ a = 0,05

Число ступенів свободи	Для критерію
двостороннього	одностороннього
	2,78	2,13
	2,57	2,01
	2,45	1,94
	2,38	1,89
	2,31	1,86
	2,23	1,81
	2,13	1,75
	2,09	1,73
	2,04	1,70
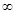
	1,96	1,64

Процедура перевірки гіпотез використовується при порівнянні вибіркових характеристик (середньої, частки, дисперсії) з відповідними нормативами, порівнянні характеристик двох вибіркових сукупностей, оцінюванні істотності розбіжностей двох розподілів, у дисперсійному та кореляційному аналізі.

Читайте також:

1. A) Оцінка захисних споруд за ємністю – визначення коефіцієнта Квм.
2. CMM. Визначення моделі зрілості.
3. DIMCLRE (РЗМЦВЛ) - колір виносних ліній (номер кольору). Може приймати значенняBYBLOCK (ПОБЛОКУ) і BYLAYER (ПОСЛОЮ).
4. I визначення впливу окремих факторів
5. II. Визначення мети запровадження конкретної ВЕЗ з ураху­ванням її виду.
6. II. Мотивація навчальної діяльності. Визначення теми і мети уроку
7. II. Фактори, що впливають на зарплату при зарубіжних призначеннях
8. ISO 15504. Призначення і структура стандарту
9. Iсторичне значення революції.
10. Ne і ne – поточне значення потужності і частоти обертання колінчастого вала.
11. Ocнoвнi визначення здоров'я
12. S Визначення оптимального темпу роботи з урахуванням динаміки наростання втоми.

Переглядів: 1547