
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Застосування подвійних інтегралів
а)обчислення площі плоскої фігури;
Площа плоскої області  дорівнює
дорівнює 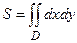 . Якщо область
. Якщо область  визначена нерівностями
визначена нерівностями 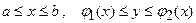 , то площа дорівнює
, то площа дорівнює  . Якщо область
. Якщо область  визначена нерівностями
визначена нерівностями
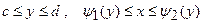 , то площа дорівнює
, то площа дорівнює 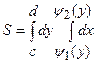 .
.
Якщо область  у полярних координатах визначена нерівностями
у полярних координатах визначена нерівностями 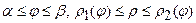 , то площа дорівнює
, то площа дорівнює 
б) обчислення об’ємів;
Об’єм циліндричного тіла, твірні якого паралельні осі 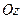 і яке обмежене знизу областю
і яке обмежене знизу областю  , що лежить на площині
, що лежить на площині 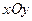 , а зверху поверхнею
, а зверху поверхнею 
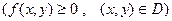 , яка неперервна в області
, яка неперервна в області  , знаходиться за формулою
, знаходиться за формулою  . Якщо циліндричне тіло обмежене зверху поверхнею
. Якщо циліндричне тіло обмежене зверху поверхнею 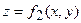 , а знизу поверхнею
, а знизу поверхнею 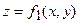 і проектується на площину
і проектується на площину 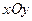 в область
в область  , то об’єм обчислюється за формулою
, то об’єм обчислюється за формулою  .
.
в) обчислення площі поверхні;
Якщо поверхня, яка задана рівнянням  , проектується на
, проектується на
площину 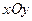 в область
в область  і функції
і функції  неперервні в цій області, то площу
неперервні в цій області, то площу 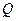 цієї поверхні знаходять за формулою:
цієї поверхні знаходять за формулою:  . Якщо поверхня має рівняння виду
. Якщо поверхня має рівняння виду 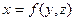 , то
, то
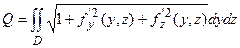 , де
, де  – проекція поверхні на площину
– проекція поверхні на площину 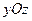 . Якщо поверхня має рівняння виду
. Якщо поверхня має рівняння виду 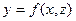 , то
, то
 , де
, де  – проекція поверхні на площину
– проекція поверхні на площину  .
.
г) маса плоскої пластини;
Нехай на площині 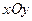 пластина займає замкнену область
пластина займає замкнену область  , в кожній точці якої відома густина
, в кожній точці якої відома густина 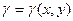 , розмірність якої
, розмірність якої  . Маса такої пластини визначиться за формулою
. Маса такої пластини визначиться за формулою 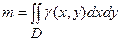
д) центр маси пластини, статичні моменти:
Центр 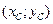 маси пластини обчислюється за формулами
маси пластини обчислюється за формулами  ,
, 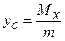 , де
, де  ,
,  – статичні моменти пластини відносно осей
– статичні моменти пластини відносно осей  та
та 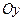 відповідно. Якщо пластина однорідна, то густина
відповідно. Якщо пластина однорідна, то густина 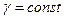 .
.
е) моменти інерції пластини;
Моменти інерції пластини  та
та  , відносно координатних осей
, відносно координатних осей  і
і 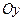 обчислюється за формулами:
обчислюється за формулами: 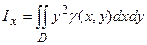 ,
, 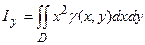 . Момент інерції пластини відносно початку координат
. Момент інерції пластини відносно початку координат 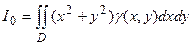 .
.
Зауваження: якщо в формулах для обчислення моментів інерції покласти  , то одержимо геометричні моменти інерції.
, то одержимо геометричні моменти інерції.
Задача 21. Обчислити площу плоскої фігури, обмежену лініями: 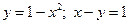 .
.
Розв’язання: Побудуємо плоску фігуру, обмежену заданими лініями. Знайдемо точки перетину ліній, що обмежують фігуру. Для
|
цього розв’яжемо систему рівнянь:
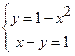 . Дістанемо
. Дістанемо 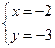 та
та  . Фігура знаходиться між двома перпендикулярами:
. Фігура знаходиться між двома перпендикулярами: 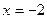 та
та  . В цей час
. В цей час 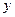 змінюється від
змінюється від 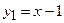 до
до  . Запишемо подвійний інтеграл через повторний (випадок I):
. Запишемо подвійний інтеграл через повторний (випадок I):

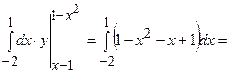
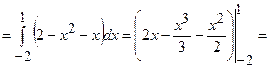
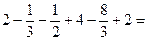 =
= 
 (кв.од.)
(кв.од.)
Задача 22. Обчислити об’єм тіла, обмеженого поверхнями 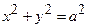 та
та 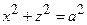 .
.
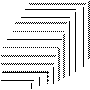
Розв’язання: Розглянемо восьму частину заданого тіла. Поверхня, яка обмежує її зверху проектується в площину 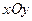 у чверть кола радіуса
у чверть кола радіуса 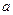 з центром в точці
з центром в точці 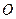 :
:
|
Для обчислення об’єму циліндричного тіла, твірні якого паралельні осі 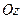 , яке обмежене знизу поверхнею
, яке обмежене знизу поверхнею  , а зверху – поверхнею
, а зверху – поверхнею 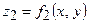 застосовують формулу:
застосовують формулу:
 . В нашому випадку
. В нашому випадку 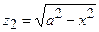 , а
, а  . Тоді
. Тоді 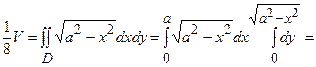
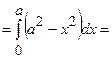
 (куб.од).
(куб.од).
Маємо 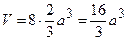 (куб.од).
(куб.од).
Задача 23. Знайти площу частини конуса 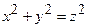 , що міститься в середині циліндру
, що міститься в середині циліндру 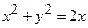 .
.
Розв’язання: Зробимо рисунок поверхні. Площу поверхні обчислимо за формулою:
 , де
, де  – проекція даної поверхні на
– проекція даної поверхні на
площину 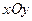 . Розв’яжемо рівняння конуса відносно
. Розв’яжемо рівняння конуса відносно  :
:
|
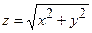 . Знайдемо частинні похідні по
. Знайдемо частинні похідні по  та
та 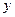 :
:
 Область
Область  у площині
у площині 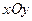 є круг, обмежений колом
є круг, обмежений колом 
Знайдемо підінтегральну функцію:

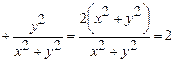 , тому
, тому  .
.
Так як область інтегрування  є круг, то перейдемо у полярну систему координат:
є круг, то перейдемо у полярну систему координат: 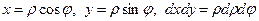 . Запишемо рівняння кола у полярних координатах:
. Запишемо рівняння кола у полярних координатах:
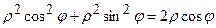 ,
,  .
.




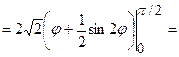
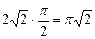 (кв. од.).
(кв. од.).
Задача 24. Знайти масу матеріальної пластини, що має форму замкненої області  , обмеженої лініями:
, обмеженої лініями:  а густина в кожній точці визначається функцією
а густина в кожній точці визначається функцією  , неперервною в області
, неперервною в області  .
.
Розв’язання: Побудуємо область 

Маса такої пластини визначається за формулою: 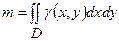 .
.
Маємо 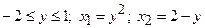 .
.
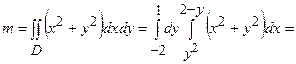
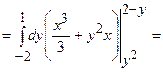

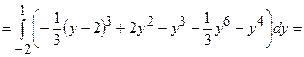
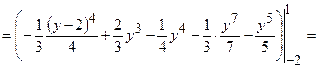
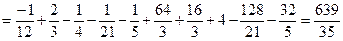 .
.
Задача 25. Знайти центр маси однорідної пластини, обмеженої кривою  та віссю
та віссю  .
.
Розв’язання: Зробимо рисунок пластини.
|
Координати 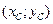 центра маси пластини обчислюється за формулами
центра маси пластини обчислюється за формулами  ,
, 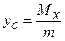 , де
, де 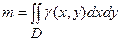 ,
,  ,
,  . Так як пластина однорідна, то
. Так як пластина однорідна, то 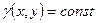 . В цьому випадку матимемо
. В цьому випадку матимемо
 .
.
Обчислимо інтеграли
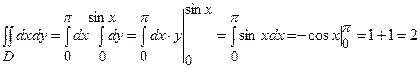 ;
;
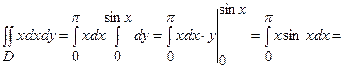
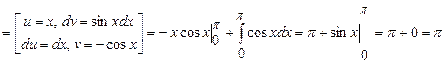
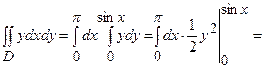
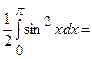
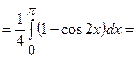
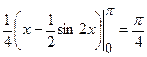 .
.
Тоді  .
.
Читайте також:
- Effects/Accessories - Ефекти/Аксесуари - Тут ви можете вибрати плагін для застосування його до ландшафту.
- I. Застосування похідної та інтеграла до роз’язування задач елементарної математики.
- IV етап. Практичне застосування одержаних даних.
- IV. ДІЯ ЦЬОГО ЗАКОНУ І ОСОБЛИВОСТІ ЙОГО ЗАСТОСУВАННЯ
- V. Виконання вправ на застосування узагальнювальних правил.
- V. Рекомендації щодо безпечного застосування сільськогосподарської техніки при виконанні основних агротехнологічних операцій у рослинництві
- А.1 Стан , та проблемні питання застосування симетричної та асиметричної криптографії.
- Автомобільні ваги із застосуванням цифрових датчиків
- Акти застосування норм права
- Акти застосування норм права в механізмі правового регулювання.
- Акти застосування юридичних норм: поняття, ознаки, види.
- Акти правозастосування, їх види
| <== попередня сторінка | | | наступна сторінка ==> |
| Подвійний інтеграл. | | | Потрійний інтеграл |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |


