
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Потрійний інтеграл
Потрійний інтеграл у декартових прямокутних координатах зводиться до обчислення трикратного інтеграла.

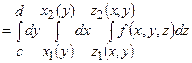 , де
, де  – циліндричне тіло, проекція якого на площину
– циліндричне тіло, проекція якого на площину 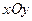 є область
є область  і яке обмежене знизу поверхнею
і яке обмежене знизу поверхнею 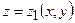 , а зверху –
, а зверху – 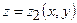 .
.
На практиці найбільш вживаними у просторі є циліндричні та сферичні координати.
Потрійний інтеграл у циліндричних координатах
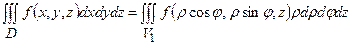 ,
,
де 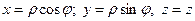 . Добуток
. Добуток 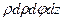 визначає елемент об’єму в циліндричній системі координат.
визначає елемент об’єму в циліндричній системі координат.
Потрійний інтеграл у сферичних координатах
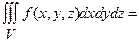
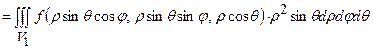 ,
,
де  ,
,  ,
,  . Добуток
. Добуток 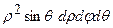 визначає елемент об’єму в сферичній системі координат.
визначає елемент об’єму в сферичній системі координат.
Задача 26. Обчислити 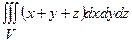 , якщо область
, якщо область  обмежена площинами:
обмежена площинами: 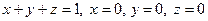 .
.
Розв’язання: Область  – піраміда, область
– піраміда, область  в площині
в площині 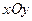 – прямокутний трикутник
– прямокутний трикутник  . Зробимо рисунок області
. Зробимо рисунок області  :
:
|


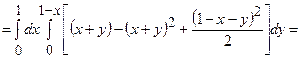
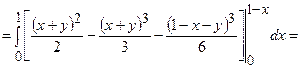

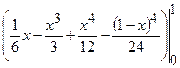 =
=
 .
.
При розв’язуванні деяких задач необхідно використовувати поверхні другого порядку. До поверхонь другого порядку відносять циліндричні, конічні поверхні, поверхні обертання, сферу, еліпсоїд, однопорожнинний та двохпорожнинний гіперболоїди, еліптичний та гіперболічний параболоїди. Розглянемо їх і наведемо канонічні рівняння та вигляд цих поверхонь.
Циліндричною поверхнеюназивають поверхню, утворену множиною прямих (твірних), які перетинають задану лінію  (напрямну). Найчастіше розглядають такі циліндричні поверхні, напрямні яких лежать в координатній площині, а твірні паралельні осі, що перпендикулярна до цієї площини. Наприклад, рівняння
(напрямну). Найчастіше розглядають такі циліндричні поверхні, напрямні яких лежать в координатній площині, а твірні паралельні осі, що перпендикулярна до цієї площини. Наприклад, рівняння  описує циліндричну поверхню з напрямними в площині
описує циліндричну поверхню з напрямними в площині 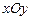 і твірними, паралельними осі
і твірними, паралельними осі 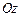 . Циліндричні поверхні, напрямними яких є криві другого порядку, називають циліндричними поверхнями другого порядку.
. Циліндричні поверхні, напрямними яких є криві другого порядку, називають циліндричними поверхнями другого порядку.
Циліндри поділяються на еліптичний 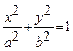 (
(  – круговий циліндр)
– круговий циліндр)

параболічний 

гіперболічний 

Поверхню, утворену обертанням заданої плоскої кривої  навколо заданої прямої (осі), розташованої в площині кривої
навколо заданої прямої (осі), розташованої в площині кривої  , називають поверхнею обертання. Розглянемо деякі з них.
, називають поверхнею обертання. Розглянемо деякі з них.
Канонічне рівняння еліпсоїда  . Числа
. Числа  називаються півосямиеліпсоїда.
називаються півосямиеліпсоїда.

Якщо  маємо сферу
маємо сферу 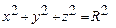 з центром в початку координат.
з центром в початку координат.
Канонічне рівняння однопорожнинного гіперболоїда


Канонічне рівняння двопорожнинногогіперболоїда 

Обидва гіперболоїди є симетричні відносно координатних площин, а початок координат точка  є їх центромсиметрії. Числа
є їх центромсиметрії. Числа  називаються півосями гіперболоїда.
називаються півосями гіперболоїда.
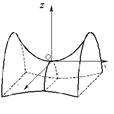
Канонічне рівняння еліптичного параболоїда 

Канонічне рівняння гіперболічного параболоїда 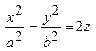
Канонічне рівняння конуса 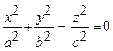

Читайте також:
- I. Застосування похідної та інтеграла до роз’язування задач елементарної математики.
- Базовою для інтегрального числення є така теорема: ТЕОРЕМА 2. Якщо функція неперервна, то для неї існує
- ВИЗНАЧЕНИЙ ІНТЕГРАЛ
- Визначений інтеграл із змінною верхнею межею
- Визначений інтеграл та його властивості
- Визначений інтеграл, як границя інтегральних сум
- Визначений інтеграл, як границя інтегральної суми. Теорема існування. Геометричний зміст визначеного інтеграла.
- Визначений інтеграл.
- Використання в економічному аналізі інтегрального методу.
- Використання інтегральної теореми
- Властивості визначеного інтеграла
- Властивості визначеного інтеграла.
| <== попередня сторінка | | | наступна сторінка ==> |
| Застосування подвійних інтегралів | | | Криволінійні інтеграли |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |
