
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Подвійний інтеграл.
Подвійний інтеграл у декартових координатах записується  , де
, де  – підінтегральна функція двох змінних
– підінтегральна функція двох змінних  та
та 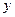 ,
,  – область інтегрування.
– область інтегрування.
Основні властивості подвійного інтеграла
а)  ;
;
б)  , де
, де  const;
const;
в) Якщо область  розбита на дві області
розбита на дві області  і
і  , які не мають спільних внутрішніх точок, то
, які не мають спільних внутрішніх точок, то
 .
.
 Подвійний інтеграл обчислюється за допомогою повторних (двократних) інтегралів.
Подвійний інтеграл обчислюється за допомогою повторних (двократних) інтегралів.
Якщо область інтегрування  обмежена двома прямими
обмежена двома прямими 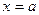 та
та  і двома неперервними кривими
і двома неперервними кривими  та
та  , кожна з яких перетинається вертикальною прямою тільки в одній точці, причому
, кожна з яких перетинається вертикальною прямою тільки в одній точці, причому  , то область
, то область 
називають правильною в напрямі осі 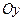 . В цьому випадку справедлива формула
. В цьому випадку справедлива формула  (випадок I).
(випадок I).
 Якщо область інтегрування
Якщо область інтегрування  обмежена двома прямими
обмежена двома прямими  та
та 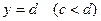 і двома неперервними кривими
і двома неперервними кривими  і
і  , кожна з яких перетинається горизонтальною прямою лише в одній точці, причому
, кожна з яких перетинається горизонтальною прямою лише в одній точці, причому  , то область
, то область  називають правильною в напрямі осі
називають правильною в напрямі осі  . В цьому випадку справедлива формула
. В цьому випадку справедлива формула
 (випадку II).
(випадку II).
У випадку I інтеграл по 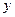 називають внутрішнім, а по
називають внутрішнім, а по  – зовнішнім; у випадку II – навпаки.
– зовнішнім; у випадку II – навпаки.
Спочатку знаходимо внутрішній інтеграл, враховуючи, що змінна інтегрування зовнішнього інтеграла є сталою, а потім знаходимо зовнішній інтеграл.
Зауваження: 1) межі інтегрування зовнішнього інтегралу завжди сталі, а межі інтегрування внутрішнього інтегралу у загальному випадку є функціями зовнішньої змінної інтегрування; 2) якщо область  є більш складною, ніж області у випадках I i II, то її необхідно розбити прямими, перпендикулярними до осі
є більш складною, ніж області у випадках I i II, то її необхідно розбити прямими, перпендикулярними до осі  (випадок I) або до осі
(випадок I) або до осі 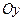 (випадок II) на такі частини, до яких можна застосувати формули наведені вище. Інтеграл по області
(випадок II) на такі частини, до яких можна застосувати формули наведені вище. Інтеграл по області  буде дорівнювати сумі інтегралів по кожній частині. 3) Якщо область
буде дорівнювати сумі інтегралів по кожній частині. 3) Якщо область  прямокутник, сторони якого паралельні осям координат, то межі інтегрування внутрішнього інтегралу є сталими.
прямокутник, сторони якого паралельні осям координат, то межі інтегрування внутрішнього інтегралу є сталими.
В деяких випадках подвійний інтеграл зручно обчислювати, перейшовши від декартової системи координат до полярної системи координат. Перехід здійснюється за формулами:  ,
,  ,
,  . Маємо
. Маємо
 .
.
 Якщо область інтегрування
Якщо область інтегрування  обмежена двома променями
обмежена двома променями  і двома кривими
і двома кривими 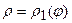 і
і 
 , то подвійний інтеграл обчислюється за формулою:
, то подвійний інтеграл обчислюється за формулою:

 .
.
Задача 16. Обчислити подвійний інтеграл  по прямокутній області інтегрування
по прямокутній області інтегрування  :
: 
 .
.
Розв’язання: 



Задача 17. Записати подвійний інтеграл через повторний, якщо область  обмежена лініями:
обмежена лініями:  .
.
Розв’язання: Побудуємо область  . Розв’яжемо системи рівнянь
. Розв’яжемо системи рівнянь 

 . Дістанемо
. Дістанемо  та
та  . Розв’язками системи є координати точок
. Розв’язками системи є координати точок  і
і  .
.
|
Область  – це трикутник
– це трикутник  . Розіб’ємо її на дві області:
. Розіб’ємо її на дві області: 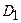 (трикутник
(трикутник 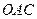 ) і
) і  (трикутник
(трикутник  ). Область
). Область 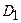 обмежена лініями:
обмежена лініями:
 ,
,
а область  обмежена лініями:
обмежена лініями: 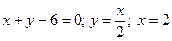 .
.
Маємо 
Тоді  .
.
Можна записати подвійний інтеграл через повторний по випадку II.
Задача 18. Змінити порядок інтегрування у повторному інтегралі.

Розв’язання: Запишемо рівняння ліній, які обмежують область інтегрування  . Для цього прирівняємо кожну змінну інтегрування до її меж інтегрування:
. Для цього прирівняємо кожну змінну інтегрування до її меж інтегрування:  . Намалюємо ці лінії.
. Намалюємо ці лінії.
|
Змінити порядок інтегрування – означає перейти від повторного інтегралу випадку I до повторного інтегралу випадку II і навпаки. Маємо повторний інтеграл випадку II. Область  знаходиться між двома прямими
знаходиться між двома прямими  ,
,  , перпендикулярними до вісі
, перпендикулярними до вісі 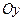 і двома неперервними лініями
і двома неперервними лініями  ,
,  . Щоб перейти до випадку I, необхідно опустити перпендикуляри на вісь
. Щоб перейти до випадку I, необхідно опустити перпендикуляри на вісь  з точок перетину ліній, що обмежують область
з точок перетину ліній, що обмежують область  . Таких перпендикулярів буде три:
. Таких перпендикулярів буде три:  . Вони розіб’ють область
. Вони розіб’ють область  на дві частини
на дві частини 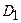 і
і  , для кожної з яких запишемо повторні інтеграли:
, для кожної з яких запишемо повторні інтеграли:
для 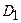 маємо
маємо  ;
;
для  маємо
маємо  .
.
Тоді:  .
.
Задача 19. Знайти інтеграл  , де
, де  :
: 
Розв’язання: Побудуємо область  . Область
. Область  – це трикутник
– це трикутник  . Маємо випадок I, тому що область
. Маємо випадок I, тому що область  знаходиться між двома прямими
знаходиться між двома прямими  ,перпендикулярними до вісі
,перпендикулярними до вісі  . Зміну змінної
. Зміну змінної  дивимось зліва направо (від лівого перпендикуляра до правого), а зміну змінної
дивимось зліва направо (від лівого перпендикуляра до правого), а зміну змінної 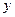 – знизу вгору (для цього рівняння лінії, через яку “входимо” в область, розв’язуємо відносно змінної
– знизу вгору (для цього рівняння лінії, через яку “входимо” в область, розв’язуємо відносно змінної 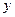 – це нижня межа інтегрування, а рівняння лінії, через яку “виходимо” з області, розв’язуємо відносно змінної
– це нижня межа інтегрування, а рівняння лінії, через яку “виходимо” з області, розв’язуємо відносно змінної 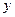 – це верхня межа інтегрування). В нашому випадку
– це верхня межа інтегрування). В нашому випадку  . Маємо
. Маємо
|


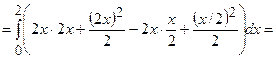

 .
.
Задача 20. Перейшовши до полярних координат, обчислити подвійний інтеграл  , якщо область
, якщо область  обмежена колами:
обмежена колами: 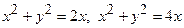 .
.
Розв’язання:
   у у
|
Побудуємо область  . Для цього запишемо рівняння кіл у канонічному вигляді:
. Для цього запишемо рівняння кіл у канонічному вигляді:  . Знайдемо центри і радіуси кіл. У заданому подвійному інтегралі перейдемо до полярної системи координат:
. Знайдемо центри і радіуси кіл. У заданому подвійному інтегралі перейдемо до полярної системи координат: 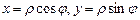 . Тоді підінтегральна функція матиме вигляд
. Тоді підінтегральна функція матиме вигляд

 . Запишемо рівняння заданих кіл в полярних координатах:
. Запишемо рівняння заданих кіл в полярних координатах:




 ;
;




 .
.
Якщо кут 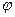 змінюватиметься на відрізку
змінюватиметься на відрізку  , то змінна
, то змінна  змінюватиметься від
змінюватиметься від  до
до  . Тоді подвійний інтеграл запишемо у полярних координатах і обчислимо його через повторний інтеграл:
. Тоді подвійний інтеграл запишемо у полярних координатах і обчислимо його через повторний інтеграл:


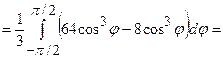
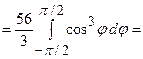


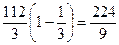
Читайте також:
- Алкени – вуглеводні, в молекулах яких є один подвійний зв’язок між атомами вуглецю . Алкені називають також олефінами або етиленовими вуглеводнями.
- Визначений інтеграл.
- З якою метою застосовують рахунки та подвійний запис господарських операцій.
- Загальний розв'язок і загальний інтеграл. Частинний та особливий розв'язки. Проміжні та перші інтеграли.
- ЛЕКЦІЯ 4. РАХУНКИ БУХГАЛТЕРС ЬКОГО ОБЛІКУ І ПОДВІЙНИЙ ЗАПИС
- Лекція №15, 16. Визначений інтеграл. Застосування визначеного інтеграла.
- Невласний інтеграл.
- Подвійний запис
- Подвійний запис і його контрольне значення
- Подвійний запис і кореспонденція рахунків
- Подвійний запис як елемент методу бухгалтерського обліку.
- Подвійний запис, його сутність і значення. Кореспонденція рахунків
| <== попередня сторінка | | | наступна сторінка ==> |
| Обчислення довжини дуги гладкої кривої. | | | Застосування подвійних інтегралів |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |


