
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Обчислення довжини дуги гладкої кривої.
а) крива задана рівнянням 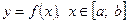 . Тоді довжина кривої обчислюється за формулою
. Тоді довжина кривої обчислюється за формулою 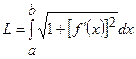 ;
;
б) крива задана параметричним рівнянням  .
.
Тоді довжина кривої обчислюється за формулою 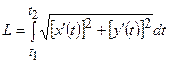 ;
;
в) крива задана рівнянням у полярних координатах 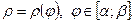 Тоді довжина кривої обчислюється за формулою
Тоді довжина кривої обчислюється за формулою 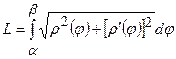 .
.
Задача 11. Знайти довжину дуги гладкої кривої.
1) крива задана рівнянням 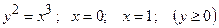
Довжину її знайдемо за формулою 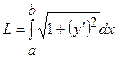 .
.
Маємо 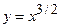 ,
, 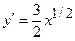 ,
, 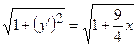 ,
, 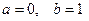 .
.
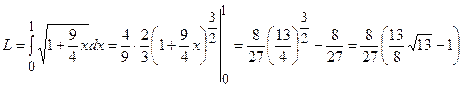 2) крива задана рівнянням
2) крива задана рівнянням  . Довжину кривої знайдемо за формулою
. Довжину кривої знайдемо за формулою 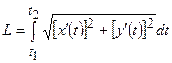 .
.
Маємо 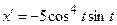 ,
, 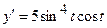 ,
,  ,
, 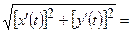
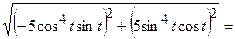

 5
5 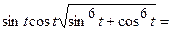
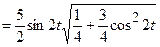
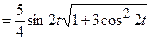

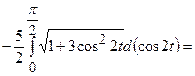

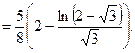
3) крива задана рівнянням 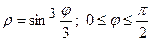 . Довжину кривої знайдемо за формулою
. Довжину кривої знайдемо за формулою  .
.
Маємо 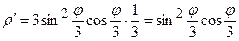 ,
, 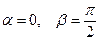 .
.
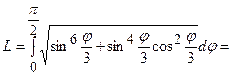
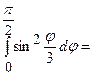
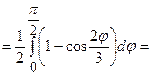
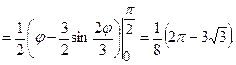
Обчислення площі поверхні, утвореної обертанням кривої навколо вісі  або
або 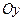 .
.
а) крива задана рівнянням 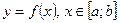 і обертається навколо вісі
і обертається навколо вісі  . Тоді площа поверхні обертання обчислюється за формулою:
. Тоді площа поверхні обертання обчислюється за формулою: 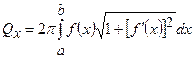
б) крива задана параметричним рівнянням  і обертається навколо вісі
і обертається навколо вісі  . Тоді площа поверхні обертання
. Тоді площа поверхні обертання
обчислюється за формулою: 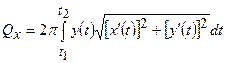
в) крива задана рівнянням у полярних координатах 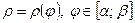 і обертається навколо полярної вісі. Тоді площа поверхні обертання обчислюється за формулою:
і обертається навколо полярної вісі. Тоді площа поверхні обертання обчислюється за формулою:  .
.
Задача 12. Обчислити площу поверхні обертання.
1) крива задана рівнянням 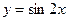 ,
, 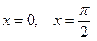 і обертається
і обертається
навколо  . Площу поверхні обертання обчислюємо за формулою:
. Площу поверхні обертання обчислюємо за формулою:
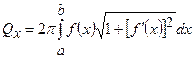 .
.
Маємо  ,
, 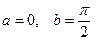
Qх = 2 
= 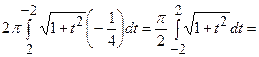
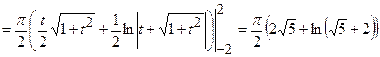
2) 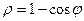 - кардіоїда обертається навколо полярної вісі. Площу поверхні обертання обчислюємо за формулою:
- кардіоїда обертається навколо полярної вісі. Площу поверхні обертання обчислюємо за формулою:
Qj = 2  . Маємо
. Маємо 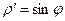 ,
, 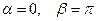 .
.
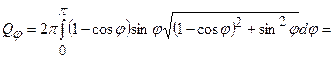
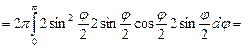
=32 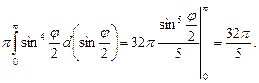
3) 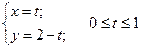 , обертається навколо
, обертається навколо  . Площу поверхні обертання обчислюємо за формулою:
. Площу поверхні обертання обчислюємо за формулою:
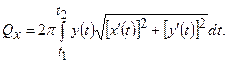 Маємо
Маємо  ,
, 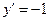 ,
, 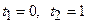 .
.
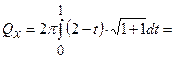
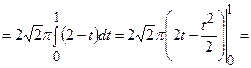
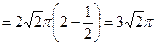 .
.
Обчислення об’єму тіла, утвореного обертанням плоскої фігури навколо вісі  або
або 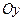 .
.
а) плоска фігура обмежена кривими: 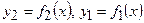 ,
, 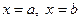
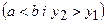 і обертається навколо вісі
і обертається навколо вісі  . Тоді об’єм тіла, утвореного обертанням плоскої фігури, обчислюється за формулою:
. Тоді об’єм тіла, утвореного обертанням плоскої фігури, обчислюється за формулою: 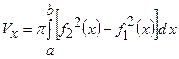 ;
;
б) плоска фігура обмежена кривою, заданою параметричним рівнянням 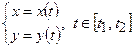 і обертається навколо вісі
і обертається навколо вісі  . Тоді об’єм тіла, утвореного обертанням плоскої фігури, обчислюється за формулою:
. Тоді об’єм тіла, утвореного обертанням плоскої фігури, обчислюється за формулою: 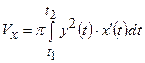 ;
;
в) плоска фігура обмежена кривою, заданою у полярних координатах 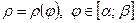 і обертається навколо полярної вісі. Тоді об’єм тіла, утвореного обертанням плоскої фігури, обчислюється за формулою:
і обертається навколо полярної вісі. Тоді об’єм тіла, утвореного обертанням плоскої фігури, обчислюється за формулою: 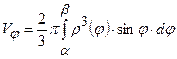 .
.
Задача 13. Обчислити об’єм тіла обертання плоскої фігури обмеженої лініями
1) 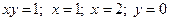 , обертається навколо
, обертається навколо  . Зробимо рисунок
. Зробимо рисунок

Об’єм тіла, утвореного обертанням плоскої фігури, обчислюємо за
формулою: 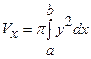 , де
, де 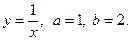
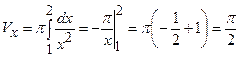 .
.
 2)
2) 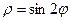 , обертається навколо полярної вісі. Зробимо рисунок .
, обертається навколо полярної вісі. Зробимо рисунок .
Об’єм тіла, утвореного обертанням плоскої фігури, обчислюємо за формулою: 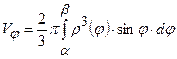 , де
, де 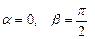 .
.
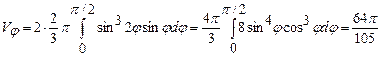 .
.
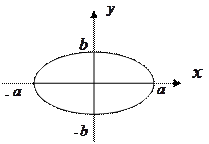 3)
3)  Обертається навколо
Обертається навколо  . Це рівняння еліпса.
. Це рівняння еліпса.
Об’єм тіла, утвореного обертанням плоскої фігури, обчислюємо за формулою: 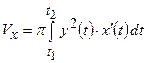 , де
, де 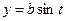 ,
, 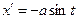 ,
, 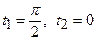 ( так як фігура симетрична відносно вісі
( так як фігура симетрична відносно вісі 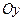 , подвоїмо результат)
, подвоїмо результат)
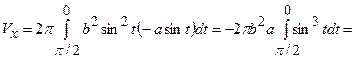
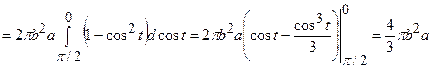 .
.
 Координати
Координати 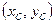 центра маси плоскої фігури обчислюються за формулами:
центра маси плоскої фігури обчислюються за формулами:  , де
, де 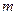 – маса плоскої фігури,
– маса плоскої фігури, 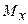 – статичний момент відносно вісі
– статичний момент відносно вісі  ,
, 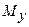 – статичний момент відносно вісі
– статичний момент відносно вісі 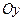 ,
, 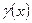 – густина плоскої фігури (
– густина плоскої фігури ( 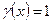 для однорідної фігури).
для однорідної фігури).
1) якщо плоска фігура обмежена лініями: 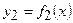
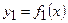 ,
, 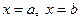
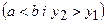 , то
, то 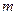 ,
, 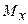 ,
, 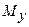 знаходимо за формулами:
знаходимо за формулами:
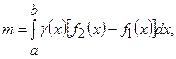
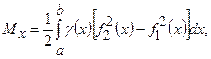
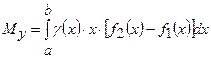 ;
;
2) якщо однорідна плоска фігура обмежена кривою, заданою
параметричним рівнянням 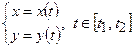 , то
, то 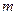 ,
, 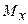 ,
, 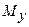 знаходимо за формулами:
знаходимо за формулами:

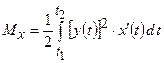 ,
,
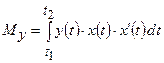 ;
;
3) якщо однорідна плоска фігура обмежена кривою, заданою рівнянням у полярних координатах 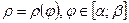 , то
, то 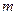 ,
, 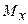 ,
, 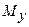 знаходимо за формулами:
знаходимо за формулами:
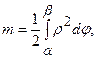
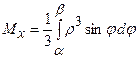 ,
,
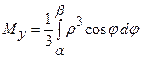 .
.
Задача 14. Знайти координати центра мас однорідної фігури, обмеженої першою аркою циклоїди 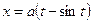 ,
, 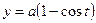
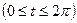 та віссю
та віссю  .
.
Знайдемо 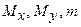 за наведеними вище формулами.
за наведеними вище формулами.
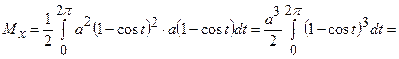
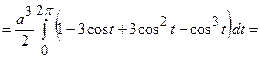
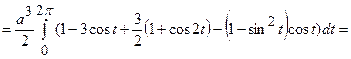
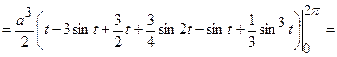
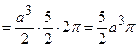 ;
;
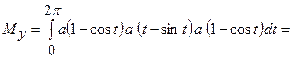
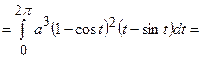
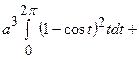


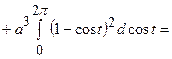
= 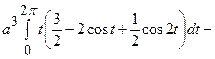
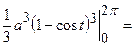
= 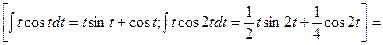
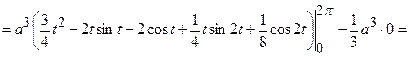
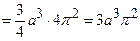 ;
;
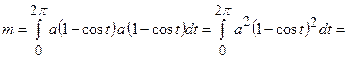
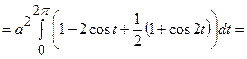
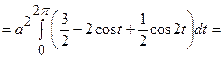
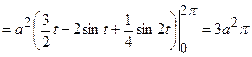

 .
.
Координати 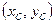 центра маси плоскої кривої обчислюються за формулами
центра маси плоскої кривої обчислюються за формулами 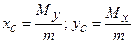 , де m – маса плоскої кривої,
, де m – маса плоскої кривої, 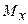 – статичний момент відносно вісі
– статичний момент відносно вісі  ,
, 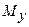 – статичний момент відносно вісі
– статичний момент відносно вісі 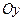 ,
, 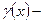 густина плоскої кривої
густина плоскої кривої 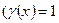 – для однорідної кривої).
– для однорідної кривої).
а) якщо плоска крива задана рівнянням 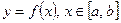 , то
, то 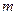 ,
, 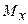 ,
, 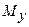 знаходимо за формулами:
знаходимо за формулами:
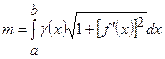 ,
,  ,
,
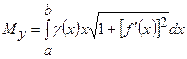 ;
;
б) якщо однорідна плоска крива задана параметричним рівнянням 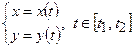 , то
, то 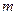 ,
, 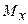 ,
, 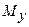 знаходимо за формулами:
знаходимо за формулами:
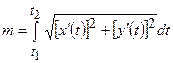 ,
, 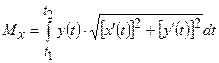 ,
,
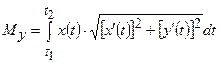 ;
;
в) якщо однорідна плоска крива задана рівнянням у полярних координатах 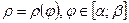 , то
, то 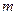 ,
, 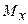 ,
, 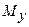 знаходимо за формулами:
знаходимо за формулами:
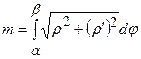 ,
, 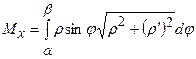 ,
,
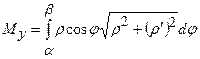 .
.
Задача 15. Знайти координати центра маси однорідної плоскої дуги півкола 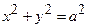 , розташованої над віссю
, розташованої над віссю  .
.
Знайдемо 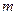 ,
, 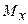 ,
, 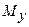 за наведеними вище формулами. Маємо
за наведеними вище формулами. Маємо
 ,
, 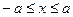 . Тоді
. Тоді 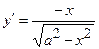 і
і
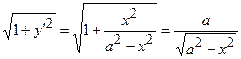 .
.
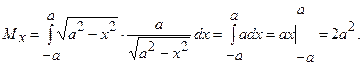
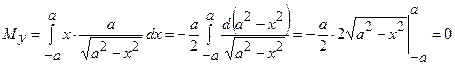
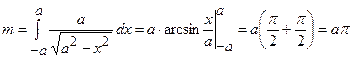
Тоді  ,
,  .
.
Визначений інтеграл застосовують для знаходження:
а) роботи 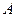 змінної сили
змінної сили  , яка діє на відрізку
, яка діє на відрізку  :
: 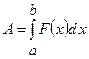 ;
;
б) шляху 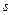 , пройденого точкою за проміжок часу від
, пройденого точкою за проміжок часу від  до
до 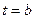 зі швидкістю
зі швидкістю  :
: 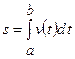 ;
;
в) маси 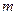 неоднорідного стержня з густиною
неоднорідного стержня з густиною 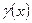 на відрізку
на відрізку
 :
: 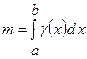 .
.
Читайте також:
- Автододавання та автообчислення.
- Алг W2 (ОБЧИСЛЕННЯ Y)
- Аналітичні показники динаміки та прийоми їх обчислення
- Асимптоти кривої.
- База оподаткування, ставки податку та порядок обчислення.
- Безпосереднє обчислення з використанням формули Ньютона-Лейбніца.
- Будівельні довжини кабелів
- Валовий національний продукт і його обчислення
- Вибір довжини і параметра перехідної кривої
- Види середніх і способи їх обчислення
- ВИЗНАЧЕННЯ ДОВЖИНИ ВІЛЬНОГО ПРОБІГУ ТА ЕФЕКТИВНОГО ДІАМЕТРУ МОЛЕКУЛ ПОВІТРЯ
- Визначення довжини лінії
| <== попередня сторінка | | | наступна сторінка ==> |
| Обчислення площі плоскої фігури. | | | Подвійний інтеграл. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |