• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Асимптоти кривої.

Означення. Пряма А наз. асимптотою кривої, якщо відстань δ від змінної т. М (х, y) кривої до цієї прямої при віддаленні т. М в ∞ → 0.

Означення. Пряма y=а наз. вертикальною асимптотою, якщо lim f(x)= ±∞ (або lim f(x)= ±∞, або lim f(x)= ±∞). Тобто вертикальні асимптоти слід шукати серед т. розриву ІІ роду.

Пряма лінія y=kx+b наз. похилою асимптотою, де k= lim 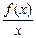, b= lim(f(x)- kх). Якщо k=0, то похилих асимптот немає.

y= b – горизонтальна асимптота.

Доведення. Нехай т. М (х, y) є l. MP ┴ NP, MP=δ, δ→0, x→∞. N(x, y) Є A, φ – кут між асимптотою і додатнім напрямом осі ОХ. В ∆ МNP MP – катет, MP=МNcos φ. МN= 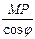. Якщо MP→0, х→∞, то МN→0, х→∞. МN= у-у= f(x)- (kх+ b).

у= kх+ b – р-ня асимптоти. Знайдемо –

lim МN= lim (f(x)- kх- b)= lim х( 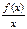-k- 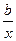)= lim х( 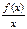-k)=0 → lim( 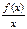-k)=0. Отже, k= lim 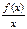. Якщо b відоме, то із рівності lim (f(x)- kх- b)=0 можна знайти b. b= lim(f(x)- kх). Таким чином, у= kх+ b – похила асимптота, k= lim 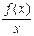, b= li

60.Найбільше і найменше значення ф-ції на відрізку.

Нехай ф-ція у=f(x) неперервна на відрізку [a,b] диференційована в кожній точці цього відрізка і має скінченне число критичних точок 1 роду на цьому відрізку.Необхідно знайти найб. та найм. Значення ф-ції на [a,b].

а)у=f(x) – монотонна (спадна або зростаюча), то найб. і найм. значення вона досягає на кінцях відрізку.

б)у=f(x) не є монотонною, то свого найб. і найм. значень на відрізку [a, b] вона може досягати в одній із критичних точок, що належ. даному відрізку.Для того, щоб знайти значення ф-ції необхідно:

1.Знайти критичні точки 1 роду.

2.Знайти значення ф-ції в критичних точках, що належать відрізку [a,b] і на кінцях відрізка.

3.Вибрати із одержаних значень найб. і найм.

Знаходження найб. і найм. значень ф-ції застосовується при рішенні багатьох практичних задач.

Первісна і невизначений інтеграл.Основні означення та найпростіші властивості невизначеного інтеграла.Таблиця інтегралів.

Нехай дано ф-цію у= f(x).Необхідно знайти таку ф-цію F(x), пох. від якої дор.f(x),тобто F’(x) = F(x).

Ф-ція F(x) наз. первісною для ф-ції F(x) на [a,b], якщо у всіх точках цього відрізку виконується рівністьF’(x)=f(x).

Первісна має наступні властивості:

1.Якщо F(x) є первісною для ф-ції f(x), то F(x)+c,c=const також є первісною для ф-ції f(x) .Дійсно (F(x)+c)’=F’(x)+0=f(x).

2.Якщо F₁(x) і F₂(x) для f(x) то F₁(x)-F₂(x)=c,c=const

Доведення

F₁(x)-F₂(x) – деяка ф-ція, що залежить від х .Тоді її похідна буде дор. F₁‘(x)-F’₂(x)=f(x)-f(x)=0 => F₁(x)-F₂(x)=c,c=const.

3.Якщо F(x) первісна f(x),то ф-ція f(ax) має первісну 1/a F(ax).Дійсно (1/aF(ax))’=1/a F’(ax)=f(ax)/

4.F(x) первісна для f(x), то ф-ція F(ax)+b) має первісну 1/bF(ax+b).Дійсно (1/aF (ax +b))’=1/aF’(ax+b)a=F’(ax+b)=f(ax+b).

Невизначеним інтегралом ф-ції F(x)на відрізку [a,b] наз. множина всіх первісних даної ф=ції на даному інтервалі виду F(x)+c де F(x) - одна із первісних, а c=const.

Властивості:

1.Похідна від невизначеного інтегралу дор. підінтегральній ф-ції.

2.Диференціал від невизначеного інтегралу дор. підінтегральному виразу.

3.Невизначений інтеграл від диференційованої ф-ції дор. цій ф-ції складеній з довільного стану.

4.Сталий множник можна виносити за знак інтегралу.

5.Сума або різниця ф-цій дор первісній суми або різниці цих ф-цій.

Таблиця інтегралів:

62.Основні методи інтегрування (безпосереднє та частинами)1

.Безпосереднє – це знаходження невизначеного інтеграла з використанням його властивостей, таблиці інтегрування інтегралів і в разі необхідності тотожних перетворень підінтегральної ф-ції.

2.Інтегрування частинами – це знаходження інтеграла за допомогою спеціальної формули, що має назву формули інтегрування частинами. ∫xdv=uv-∫vdu. d(uv)=(uv)’dx=(u’v+uv’)dx=u’vdx+uv’dx=vdu+udv. ∫d(uv)= ∫vdu+∫udv. Uv=∫vdu+∫udv.

Ця формула заст. в тих випадках, коли під знаком інтегралу знах. добуток двох функцій: алгебраїчної та геометричної. Вираз розділяється на дві частини, які позначаються через “u” та “dv”. Після цього виконуємо обчислення за формулою.

63.Інтегруваання методом заміни змінної.

Нехай потрібно знайти ∫f(x)dx, причому безпосередньо підібрати первісну F(x) для ф-ї f(x) не можемо,але знаємо, що вона існує. Зробимо заміну змінної в підінтегральний вираз: нехай x=j(t) де j(t) – неперервна, з неперервною похідною, яка має обернену ф-ю dx=j’(t)dt. Доведемо, що в цьому випадку має місце наступна формула ∫f(x)dx=∫f(j(t)*j’(t)dt). Проінтегруємо ліву і праву частини формули. (∫f(x)dx)’_x=f(x)

∫f(j(t)j’(t)dt)’_x=f(j(t))j’(t)t’_x

dx=j’(t)dt dx/dt=j’(t) dt/dx=1/j’(t)

Тоді,маємо f(j(t))j’*1/j’(t)=f(j(t))

Таким чином ми показали, що похідні від лівої і пр. частини рівні.

Читайте також:

1. Асимптоти гіперболи
2. Асимптоти графіка функції
3. Асимптоти графіка функції
4. Асимптотична нормальність й ЦПТ
5. Асимптотичний підхід до порівняння оцінок
6. Кривизна плоскої кривої.
7. Крипто перетворення НШ в групі точок еліптичної кривої.
8. Опуклість та вгнутість кривої. Точки перегину

Переглядів: 1230