• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Крипто перетворення НШ в групі точок еліптичної кривої.

Основним недоліком крипто перетворень НШ в полі Галуа є субекспоненційний характер складності атаки дискретного логарифмування при спробі порушника визначити особистий ключ, тобто вирішення рівняння (3.19) відносно x_i. Як підтвердив досвід застосування вказане протиріччя може бути вирішене при застосуванні криптографічних перетворень в групі точок еліптичної кривої, в тому числі для НШ [11,12, 42, 43]. При цьому особливо широке застосування воно знайшло в криптографічних протоколах[65,43,43]. Також необхідно відмітити, що НШ в групі точок еліптичної кривої є розвитком НШ в полі Галуа, та майже повністю повторяє загальну схему.

Розглянемо сутність асиметричних крипто перетворень НШ в групі точок еліптичної кривої [7–10, 44, 40, 46, 64]. Перед вивченням цього матеріалу рекомендується, покрайній мірі, ознайомитись з пунктом 1.3 , тобто математичним апаратом еліптичних кривих. Також звернемо на крипто перетворення в групі точок еліптичної кривої суттєву увагу, так як перетворення в групі точок витримали випробовування часом, а складність атаки визначення ключа( крипто атаки « повне розкриття) до цих пір носить експоненційний характер.

Розгляд будемо вести в такій послідовності:

- перелік та сутність загальних параметрів;

- генерування асиметричної ключової пари;

- направлене зашифрування блоків інформації;

- направлене розшифрування криптограм;

- попередня оцінка криптографічної стійкості.

Перелік та сутність загальних параметрів. У 90-х роках було запропоновано використовувати крипто перетворення, що базуються на перетвореннях у групі точок еліптичних кривих над полями F(p), F(2m), F(pm) [44–52, 30–32, 7–10, 35, 46, 51, 64]. Основні положення та математичні методи криптографічних перетворень у групі точок еліптичних кривих наведено в 1.3 цієї монографії.

До загальних параметрів еліптичної кривої на полем Галуа F ( Р) відноситься кортеж

( а, в, G, n, P, u, h) , (2.28)

де:

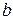- та параметри еліптичної кривої, які визначають рівняння еліптичної кривої , що використовується ;

- - базова точка порядку 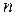з координатами та;

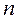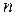- порядок базової точки за умови, що та - просте число;

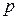- - розмір поля, який визначає базове кінцеве поле , де 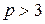повинно бути, простим числом;

- u = 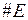- порядок еліптичної кривої;

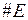- коефіцієнт взаємозв’язку порядку кривої та порядку базової точки , причому .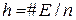

До загальних параметрів еліптичної кривої на полем Галуа F ( 2^m) відноситься кортеж

( а, в, G, n, ( f(x), m),u, h) , (2.29)

де:

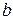- та параметри еліптичної кривої, які визначають рівняння еліптичної кривої , що використовується ;

- - базова точка порядку 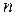з координатами та;

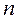- базової точки при умові, що та 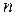- просте число;

( f(x), m) – примітивний поліном та його степінь;

- u = 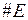- порядок еліптичної кривої;

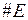- коефіцієнт взаємозв’язку порядку кривої та порядку базової точки , причому .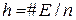

Крива, тобто її параметри, ні в якому випадку не повинні вибиратись із переліку значень, що не рекомендуються або заборонені.

До загальних параметрів еліптичної кривої на полем Галуа F ( р^m) відноситься кортеж

( а, в, G, n, рm ,u, h) , (2.30)

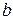та параметри еліптичної кривої, які визначають рівняння еліптичної кривої , що використовується : ;

базова точка порядку 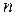з координатами та;

порядок базової точки при умові, що та 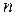- просте число;

розмір поля, який визначає базове кінцеве поле , де 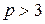повинно бути простим числом;

кофактор взаємозв’язку порядку кривої u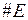 та порядку базової точки причому .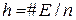

Крива, тобто її параметри, ні в якому випадку не повинні вибиратись із переліку значень, що не рекомендуються або заборонені.

Усі параметри еліптичної кривої повинні генеруватись випадково. Для цього в рекомендується використовувати випадкові бітові рядки SEED. Це відноситься до генерації загальних параметрів еліптичних кривих над скінченними полями. Вибір способів та засобів генерування SEED повинен здійснюватись з урахуванням вимог законодавства(див . розділ 5).

Генерування асиметричної ключової пари. Ключова пара

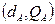, (3.31)

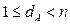де: особистий ключ, генерується випадково, а відкритий ключ обчислюється засобом виконання скалярного множення, тобто цілого числа та точку еліптичної кривої

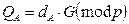, (3.32 )

де G – базова точка на еліптичній кривій порядку n, а QA – відкритий ключ, що є точкою на еліптичній кривій з координатами (ха, уа).

Існує тривимірне подання ЕК, що називається проективною геометрією (базисом). У проективній геометрії кожна точка задається трьома координатами – X, Y, Z.

Основною операцією в групі точок ЕК є скалярне множення вигляду (3.32) для простого поля F(p), а для розширення F(2):

. (3.33)

Стійкість атаки проти загрози повного розкриття визначається складністю розв’язання порівнянь (3.32) і (3.33) відносно особистого ключа d. Складність розв’язування цього рівняння набагато вища, ніж у кільці та полі. У полі – субекспоненційна, а в групі точок еліптичних кривих – експонентна складність.

Направлене зашифрування блоків інформації. Нехай мається повідомлення М, розбиваємо його на блоки , довжина яка задовольняє вимоги 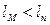, тобто менше довжини модуля ln, . Зашифрування здійснюється за правилом

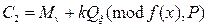, (3.34)

де:

- k – ключ сеансу (сеансовий);

- - відкритий ключ отримувача.

Також обчислюється відкритий ключ сеансу(зашифрування блоку інформації)

, (3.35)

де G – базова точка на еліптичній кривій.

Далі відправник передає користувачеві одержувачеві два блоки:

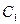- - відкритий ключ сеансу;

- - блок криптограма.

Направлене розшифрування криптограми. Розшифрування криптограми здійснюється за умови що:

одержувач володіє особистим ключем ;

знає загальні параметри;

отримав та має достовірні значення пари ( С1 , С2)

Розшифрування виконується у такій послідовності.

Користувач бере 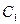, що повинна бути точкою на еліптичній кривій та знаходить

(3.36 )

Далі отриману точку він віднімає від криптограми С2, тобто обчислює

(3.37)

Таким чином, криптографічне перетворення в групі точок еліптичної кривої є зворотнім та однозначним.

Попередня оцінка криптографічної стійкості. Зробимо попередні оцінки криптографічної стійкості на основі розгляду атаки типу «повне розкриття». Для цього розглянемо

проблему розв’язання дискретного логарифма на еліптичних кривих. Нехай є точки ЕК , необхідно вирішити рівняння (3.32) чи (3.33)відносно d, тобто для загального випадку еліптичної кривої над полем F (pm) рівняння

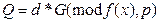(3.38)

відносно особистого ключа або довести, що рішення не існує. Необхідна умова, що має бути виконана – 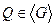, тобто 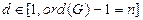, значить n= , де – базова точка, що формує групу, – порядок базової точки 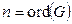, – відкритий ключ, – точка нескінченності, операція « » визначає скалярне множення на еліптичній кривій.

Проблемні питання НШ в групі точок еліптичної кривої.

1).Проблемність в тому, що повинно бути точкою на ЕК. Тобто, перед зашифруванням блоки інформації необхідно подати у вигляді точок еліптичної кривої. Ця задача хоча і є поліноміально складною, але за складністю має той же порядок що і шифрування. Вказане зменшує швидкодію НШ.

2). Недоліком загаль­ного алгоритму є те, що він має дуже велику складність для кожного блоку по­трібно генерувати k і виконувати скалярне множення для обчислення виразів k G та .

Читайте також:

1. А.1 Стан , та проблемні питання застосування симетричної та асиметричної криптографії.
2. Адаптивні хвилькові перетворення : Хвилькові пакети.
3. Визначення висоти точок
4. Визначення перетворення за Лапласом
5. Визначення. Матриці, отримані в результаті елементарного перетворення, називаються еквівалентними.
6. Визначте соціальні перетворення в процесі радянізації українського суспільства.
7. Виконаємо лінійне перетворення
8. Вимірювальні сигнали, перетворення вимірювальних сигналів, форми вимірювальної інформації
9. Вирішення проблеми не міститься в існуючому знанні та не може бути отримане шляхом перетворення наявної наукової інформації.
10. Вирішення проблеми не міститься в існуючому знанні та не може бути отримане шляхом перетворення наявної наукової інформації.
11. Виховна робота в академічній групі
12. Вібрація – це механічні коливання матеріальних точок або тіл, які виникають в горизонтальному і вертикальному напрямах.

Переглядів: 1891