• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Крипто перетворення НШ в полі Галуа

Додаток А Стан , та проблемні питання застосування симетричної та асиметричної криптографії.

Проблемні питання направленого шифрування на ідентифікаторах.

Криптографічне перетворення зі спарюванням точок еліптичних кривих.

Крипто перетворення НШ в групі точок еліптичної кривої.

Крипто перетворення НШ в полі Галуа

Асиметричні крипто перетворення та їх застосування

для забезпечення конфіденційності »

Навчальні питання

Джерела, що рекомендуються до самостійної роботи

1. Горбенко І.Д., Горбенко Ю.І. Прикладна криптологія. Монографія (електронний варіант). Харків, ХНУРЕ, 2011 р.

2. Горбенко І.Д., Горбенко Ю.І. Прикладна криптологія. Електронний конспект лекцій. Харків, ХНУРЕ, 2011 р.

3. Горбенко І. Д. Гриненко Т. О. Захист інформації в інформаційно-телекомунікаційних системах: Навч. посібник. Ч.1. Криптографічний захист інформації - Харків: ХНУРЕ, 2004 - 368 с.

4. Горбенко Ю.І., Горбенко І.Д. Інфраструктури відкритих ключів . Системи ЕЦП. Теорія та практика. Харків. Форт. 2010 , 593с.

Додаткова література

1.В. Задірака . Компьютерная криптологія. Підручник. К, 2002 ,504с.

2. А. Менезис, П. Ван Аршот, С. Ватсон. Руководство по прикладной криптографии CRC Press, 1997, электронная копия, 662 с

10. Брюс Шнайер. Прикладная криптография. М., изд. Триумф. 2002 г., 797 с

Розглянемо сутність асиметричних крипто перетворень в полі Галуа на прикладі направленого шифрування [7–10, 44, 40, 46, 64].

Використання загальних параметрів та генерування асиметричної ключової пари. Нехай є просте поле Галуа F(p). Третя довірена сторона генерує загальні параметри , де - просте, як правило «сильне» просте число, а - первісний елемент. Далі всі користувачі генерують випадково по принципу « сам – собі» 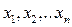- особисті ключі і зберігають їх як таємні, де

_i. (3.18)

Потім кожен формує відкриті ключі, викори­стовуючи загальносистемні параметри , тобто кожен із користувачів обчислює свій відкритий ключ

(3.19 2)

Кожний первісний елемент породжує поле 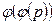ізоморфізмів поля Галуа

.

Приклад генерування ключів для двох користувачів наведений в таблиці 3.6

Таблиця 3.6

Генерування асиметричної пари ключів у полі Галуа

А		В
ХА		ХВ

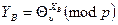
Відкритий ключ сертифікують, тобто виготовляють сертифікат відкритого ключа

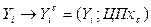, (3.20 3)

де - особистий ключ сертифікації третьої довіреної сторони.

Створюється база всіх сертифікатів і до неї добавляється ключ сертифі­кації центра, разом з загальними параметрами.

(3.21 4)

Алгоритм зашифрування. Нехай потрібно направлено зашифрувати повідомлення М, яке розбивається на блоки довжиною. Алгоритм зашифрування здійснюється таким чином.

1). Генерується особистий ключ сеансу зашифрування

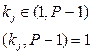, причому (3.22)

2). Обчислюється відкритий ключ сеансу

(3.23 5)

3). Обчислюється відкритий ключ направленого шифрування

(3.24 6)

- відкритий ключ одержувача.

4). При за шифруванні користувач А використовуючи свій ключ сеансу k_a та - відкритий ключ одержувача В, і зрозуміло, загальні параметри , обчислює блок - криптограму Сi, а також відкритий ключ сеансу

, (3.25 1.8)

де 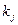– особистий ключ сеансу того хто зашифровує.

Далі користувач А передає користувачу В пару .

Алгоритм розшифрування блока криптограми . Розшифрування користувачем здійснюється таким чином.

1). Користувач В має загальні параметри , що ідентичні користувачеві А.

2) Потім користувач В направлено розшифровує криптограму з використанням свого особистого ключа Х_В, поділивши на , тобто

. (3.26 1.9)

3). Якщо помилок в криптограмі та відкритому ключі сенсу немає, та застосовується правильно особистий ключ Х_В, то користувач В отримує відкритий блок – повідомлення .

Таким чином, криптографічне перетворення в полі Галуа є зворотнім та однозначним.

Проблемні питання криптографічних перетворень в полі Галуа. Як і відносно RSA так і відносно криптографічних перетворень в полі Галуа існує ряд проблемних питань, завдяки яким це перетворення виводиться із застосування, в тому числі такі[ ].

1). Основним недоліком НШ з використанням перетворень в полі Галуа, як і для RSA, є велика довжина модуля перетворення Р та довжини ключів, при яких забезпечується задекларований рівень криптографічної стійкості, так нині рекомендується довжина модуля не менше 2048 бітів.

2). Отримані теоретичні та практичні результати факторизації , перше за все у вигляді решета числового поля, якими підтверджено субекспоненціальний характер складності факторизації. Так для двійкового та загального решіт числового поля складність крипто аналізу може бути оцінена як:

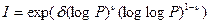, (3.27 18)

– параметри методу. Наприклад, для загального решета числового поля δ=1,90(2.06) , ν=1/3.

3) Необхідність постійного збільшення з метою забезпечення допустимого рівня стійкості довжини модулі Р криптографічного перетворення, так нині рекомендується довжина модуля не менше 2048 бітів, що створює проблеми відносно форматів, стандартизації, апаратної реалізації тощо.

4) Збільшення довжини ключів асиметричної пари (х_i, Y_i) практично до довжини модуля, причому відкритого обов’язково, що викликає підвищення складності прямих та зворотних криптографічних перетворень, а також проблемні питання з форматами та уніфікацією.

5) Просте число Р - модуль криптографічного перетворення, має бути не просто простим, а сильним простим числом, в широкому чи вузькому змістах[ ].

6) В цілому складність крипто аналізу в полі, наприклад в системі Ель - Гамаля, ґрунтується на складності визначення особистого ключа і інформації , при знанні відкритих параметрів Р, і ключа . Складність крипто аналізу визначається складністю рішення дискретного логарифма , і визначення значення повідомлення із співвідношення .

В певній мірі зазначені недоліки значною мірою можуть бути усунуті за рахунок криптографічного перетворення в полі Галуа за двома модулями, наприклад P та q .

В якості прикладу розглянемо криптографічне перетворення Ель - Гамаля за двома модулями P та q[ ], яке може застосовуватись як для цифрового підпису так і направленого шифрування та в криптографічних протоколах (див розділи 6 та 7). Загальносистем­ними параметрами є для DSA [ ]або для ГОСТ 34.310-95[ ], де Р є просте «сильне» число, q – також просте число, але яке входить в канонічний розклад числа (Р – 1), а – первісний елемент простого поля.

Читайте також:

1. А.1 Стан , та проблемні питання застосування симетричної та асиметричної криптографії.
2. Адаптивні хвилькові перетворення : Хвилькові пакети.
3. Визначення перетворення за Лапласом
4. Визначення. Матриці, отримані в результаті елементарного перетворення, називаються еквівалентними.
5. Визначте соціальні перетворення в процесі радянізації українського суспільства.
6. Виконаємо лінійне перетворення
7. Вимірювальні сигнали, перетворення вимірювальних сигналів, форми вимірювальної інформації
8. Вирішення проблеми не міститься в існуючому знанні та не може бути отримане шляхом перетворення наявної наукової інформації.
9. Вирішення проблеми не міститься в існуючому знанні та не може бути отримане шляхом перетворення наявної наукової інформації.
10. Властивості зворотного перетворення за Лапласом
11. Властивості прямого перетворення за Лапласом
12. Вплив легуючих елементів на перетворення в сталі

Переглядів: 872