
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Опуклість та вгнутість кривої. Точки перегину
Нехай функція  визначена на інтервалі
визначена на інтервалі 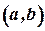 і в кожній точці цього інтервалу має скінчену похідну. Тоді в кожній точці
і в кожній точці цього інтервалу має скінчену похідну. Тоді в кожній точці  графіка цієї функції можна провести дотичну, не паралельну осі
графіка цієї функції можна провести дотичну, не паралельну осі  . Крива, яка є графіком цієї функції, називається гладкою.
. Крива, яка є графіком цієї функції, називається гладкою.
Якщо крива, яка є графіком функції  , розміщена не нижче будь-якої дотичної на інтервалі
, розміщена не нижче будь-якої дотичної на інтервалі 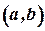 , то вона називається вгнутою догори або просто вгнутою на цьому інтервалі. Іноді її ще називають опуклою вниз (рис. 25).
, то вона називається вгнутою догори або просто вгнутою на цьому інтервалі. Іноді її ще називають опуклою вниз (рис. 25).
Якщо крива, яка є графіком функції  , розміщена не вище будь-якої дотичної на інтервалі
, розміщена не вище будь-якої дотичної на інтервалі 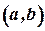 , то вона називається вгнутою донизу або просто опуклою на цьому інтервалі. Таку криву ще називають опуклою вгору (рис. 26).
, то вона називається вгнутою донизу або просто опуклою на цьому інтервалі. Таку криву ще називають опуклою вгору (рис. 26).
 |
Точка  називається точкою перегину гладкої кривої
називається точкою перегину гладкої кривої  , якщо існує
, якщо існує 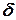 -окіл точки
-окіл точки 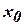 такий, що в інтервалах
такий, що в інтервалах  і
і  крива
крива  має опуклість різних напрямків (рис. 27).
має опуклість різних напрямків (рис. 27).
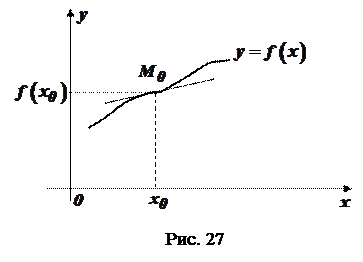
У цьому випадку графік функції  в інтервалах
в інтервалах  і
і  лежить по різні боки від дотичної, проведеної в точці
лежить по різні боки від дотичної, проведеної в точці  .
.
Теорема. Нехай функція  визначена на інтервалі
визначена на інтервалі 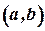 і в кожній точці цього інтервалу має похідні до другого порядку включно. Тоді, якщо
і в кожній точці цього інтервалу має похідні до другого порядку включно. Тоді, якщо  у всіх точках
у всіх точках 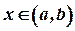 , то графік функції
, то графік функції  на інтервалі
на інтервалі 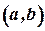 вгнутий (опуклий вниз), якщо ж
вгнутий (опуклий вниз), якщо ж  у всіх точках
у всіх точках 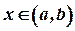 , то графік функції
, то графік функції  на інтервалі
на інтервалі 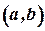 опуклий (опуклий вгору).
опуклий (опуклий вгору).
Доведення.  в інтервалах
в інтервалах  і
і  лежить по різні боки від дотичної, проведеної в точці
лежить по різні боки від дотичної, проведеної в точці  .
.
Нехай  . Виберемо точку
. Виберемо точку  і покажемо, що графік функції
і покажемо, що графік функції  лежить не нижче дотичної, яка проходить через точку
лежить не нижче дотичної, яка проходить через точку  . Щоб відрізняти ординату графіка функції і ординату дотичної, останню будемо позначати буквою
. Щоб відрізняти ординату графіка функції і ординату дотичної, останню будемо позначати буквою  . Запишемо рівняння дотичної в точці
. Запишемо рівняння дотичної в точці  :
:
 (1)
(1)
Оскільки функція  має похідні до другого порядку включно, то згідно формули Тейлора (при
має похідні до другого порядку включно, то згідно формули Тейлора (при 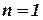 ) маємо:
) маємо:
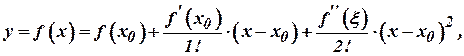 (2)
(2)
де  . Віднімемо від рівності (2) рівність (1)
. Віднімемо від рівності (2) рівність (1)
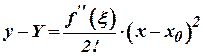 .
.
Оскільки 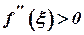 , то
, то  , тобто
, тобто 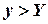 . Отже, графік функції
. Отже, графік функції  у будь-якій, відмінній від
у будь-якій, відмінній від 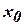 , точці
, точці 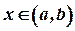 лежить вище дотичної, проведеної до нього в точці з абсцисою
лежить вище дотичної, проведеної до нього в точці з абсцисою 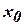 .
.
Аналогічно доводиться теорема для випадку  .
.
Установимо необхідну умову існування точки перегину графіка функції  . Нехай функція
. Нехай функція  визначена і має неперервні похідні до другого порядку включно на інтервалі
визначена і має неперервні похідні до другого порядку включно на інтервалі 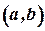 . Тоді. Якщо в кожній точці
. Тоді. Якщо в кожній точці 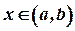
 , то графік функції
, то графік функції  на інтервалі
на інтервалі 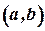 вгнутий (опуклий вниз). Якщо
вгнутий (опуклий вниз). Якщо  ,
, 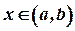 , - то графік опуклий (опуклий вгору).
, - то графік опуклий (опуклий вгору).
Отже, якщо на інтервалі 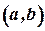
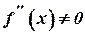 , то графік функції
, то графік функції  точок перегину на цьому інтервалі не має. Таким чином, точка
точок перегину на цьому інтервалі не має. Таким чином, точка  , де
, де  може бути точкою перегину графіка функції
може бути точкою перегину графіка функції  лише в тому випадку, коли
лише в тому випадку, коли 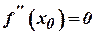 .
.
Отже, умова 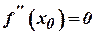 є необхідною, для того, щоб точка
є необхідною, для того, щоб точка  була точкою перегину графіка функції
була точкою перегину графіка функції  .
.
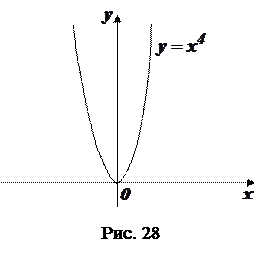 Покажемо, що не всяка точка
Покажемо, що не всяка точка  за умови
за умови 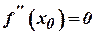 є точкою перегину. Розглянемо такий приклад: Нехай
є точкою перегину. Розглянемо такий приклад: Нехай  . Тоді
. Тоді 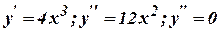 при
при  . Але точка
. Але точка  не є точкою перегину графіка функції
не є точкою перегину графіка функції  (рис. 28).
(рис. 28).
Установимо достатню умову існування точки перегину графіка функції  . Нехай точка
. Нехай точка  така, що
така, що 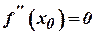 й існує таке
й існує таке 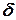 , що в інтервалах
, що в інтервалах  і
і  друга похідна
друга похідна 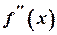 має різні знаки. Тоді точка
має різні знаки. Тоді точка  є точкою перегину. Дійсно, за вказаних умов у інтервалах
є точкою перегину. Дійсно, за вказаних умов у інтервалах  і
і  крива
крива  має опуклість різних напрямків. Отже, точка
має опуклість різних напрямків. Отже, точка  є точкою перегину цієї кривої.
є точкою перегину цієї кривої.
Зауваження. Точка  є точкою перегину графіка функції
є точкою перегину графіка функції  і в тому випадку, коли в точці
і в тому випадку, коли в точці  існує дотична до графіка функції
існує дотична до графіка функції  , друга похідна в самій точці
, друга похідна в самій точці 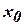 не існує, але існує в деякому
не існує, але існує в деякому 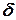 -околі точки
-околі точки 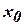 , причому в інтервалах
, причому в інтервалах  і
і  має різні знаки.
має різні знаки.
Це установлюється аналогічно попередньому.
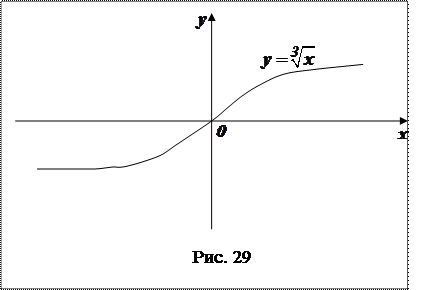 Приклад. Нехай
Приклад. Нехай 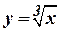 . Ця функція в точці
. Ця функція в точці  має нескінченну похідну першого порядку й дотична до її графіка в точці
має нескінченну похідну першого порядку й дотична до її графіка в точці  співпадає з віссю
співпадає з віссю  . Друга похідна в точці
. Друга похідна в точці  не існує. Графік функції
не існує. Графік функції 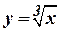 в точці
в точці  має перегин, оскільки справа і зліва від точки
має перегин, оскільки справа і зліва від точки  друга похідна
друга похідна  має різні знаки (рис. 29).
має різні знаки (рис. 29).
Читайте також:
- Алгебраїчний спосіб визначення точки беззбитковості
- Аналіз точки беззбитковості
- Видалення характерної точки
- Визначення точки
- Визначення точки беззбитковості
- Визначення точки беззбитковості.
- Визначення. Точки максимуму й мінімуму функції називаються точками екстремуму.
- Відстань від точки до площини і від точки до прямої на площині
- Диференціальні рівняння руху вільної матеріальної точки
- Енергетичні рівні напівпровідникової квантової точки
- З точки зору динамічного підходу механізм соціального конфлікту проходить зазвичай наступні стадії протікання конфлікту.
- З точки зору цілей, які відстоюють протидіючі сторони конфлікту розподіляються на особисті, групові, суспільні.
| <== попередня сторінка | | | наступна сторінка ==> |
| Розв’язування. | | | Асимптоти графіка функції |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |