• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Основні властивості криволінійного інтеграла першого роду

а) криволінійний інтеграл першого роду не залежить від напрямку шляху інтегрування: ;

б) ;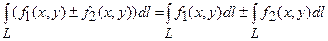

в) , де k = const ;

г) якщо крива 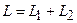, то

;

Криволінійний інтеграл першого роду при обчисленні зводиться до визначеного інтегралу:

а) якщо крива 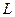задана рівнянням 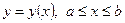, то

;

б) якщо крива 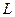задана параметричним рівнянням , , то ;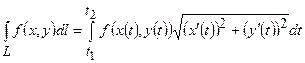

в) у випадку просторової кривої , яка має рівняння

матимемо

;

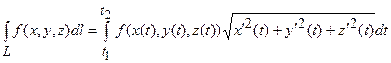Криволінійний інтеграл першого роду застосовують для знаходження:

а) обчислення довжини кривої 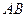здійснюється за формулою: ;

б) якщо циліндрична поверхня, твірні якої паралельні осі 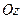, опирається на криву 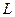в площині 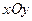, а зверху обмежена поверхнею , то площа такої циліндричної поверхні обчислюється за формулою: ;

в) маса матеріальної кривої обчислюється за формулою: , де – лінійна густина;

г) координати 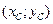центра маси кривої 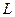знаходяться за формулами:

,

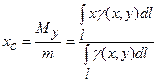
де 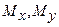– статичні моменти кривої відносно осей і 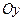. У випадку, коли розглядається однорідна матеріальна крива, слід покласти ;

д) моменти інерції кривої відносно осей і

початку координат обчислюються за формулами:

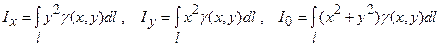
Задача 27. Обчислити криволінійний інтеграл першого роду 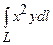, де 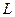– частина кола 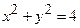, розміщена в першій чверті .

Розв’язання: Запишемо рівняння кола у вигляді 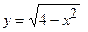, 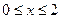. Знайдемо : ,

.

Тоді .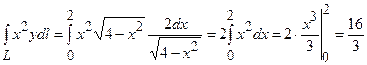

Криволінійний інтеграл другого роду (по координатах) це 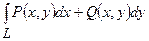, де функції , 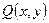визначені і обмежені на кривій .

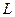Основні властивості криволінійного інтеграла другого роду:

а) криволінійний інтеграл другого роду змінює свій знак на протилежний при зміні напрямку шляху інтегрування

;

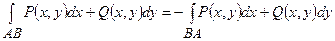б) ;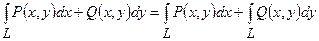

Інші властивості аналогічні властивостям інтеграла першого роду.

Криволінійний інтеграл другого роду при обчисленні зводиться до визначеного інтегралу:

а) якщо крива 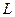задана рівнянням 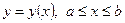, то

;

б) якщо крива 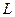задана параметричним рівнянням , , то

;

в) криволінійний інтеграл другого роду залежить від шляху інтегрування:

;

Якщо , то значення інтеграла не залежить від форми кривої 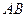, яка сполучає точки 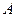та і , а вираз – повний диференціал функції , яку можна відновити використовуючи формули:

або

,

де довільна фіксована точка, в якій визначені функції і .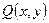

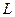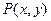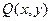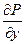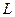Якщо – замкнений контур, який обмежує область і функції і неперервні, разом із своїми частинними похідними 1-го порядку: і в замкненій області включаючи межу , то справедлива формула Гріна:

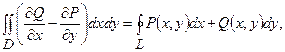
де обхід контуру 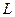вибирається таким, щоб область залишалась зліва.

Криволінійний інтеграл другого роду застосовують для знаходження:

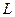а) площі плоскої фігури , обмеженої кривою , за формулою: ;

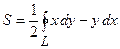б) роботи сили 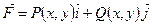при переміщенні матеріальної точки вздовж кривої : .

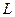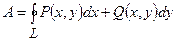Задача 28. Обчислити криволінійний інтеграл другого роду , де 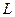– замкнений контур, утворений лініями .

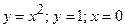Розв’язання: Для замкненого контуру існує лише два напрями

обходу: проти стрілки годинника ( додатна орієнтація контуру) та за стрілкою годинника (від¢ємна орієнтація контуру). При додатній орієнтації контуру він завжди залишається зліва при його обході.

Маємо:

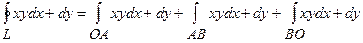
1) рівняння : 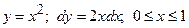, тоді

;

2) рівняння 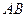: , змінюється від 1 до 0, тоді

;

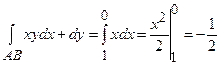3) рівняння : , 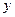змінюється від 1 до 0, тоді

;

Тоді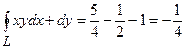

Задача 29. Впевнитись, що вираз

є повним диференціалом деякої функції і знайти цю функцію.

Розв’язання: З даного виразу випливає , . Знайдемо частинні похідні , .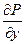

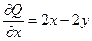, . Оскільки , то вираз дійсно є повним диференціалом деякої функції 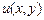. Знайдемо цю функцію за допомогою формули

.

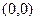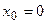В якості точки можна взяти точку : , . Тоді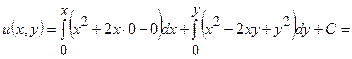

.

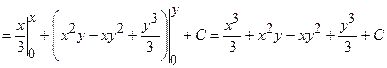Читайте також:

1. I. Застосування похідної та інтеграла до роз’язування задач елементарної математики.
2. I. ОСНОВНІ ЕТАПИ ВИКОНАННЯ КУРСОВОЇ РОБОТИ
3. II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
4. II. Основні засоби
5. II. ОСНОВНІ ПОВНОВАЖЕННЯ ТРУДОВИХ КОЛЕКТИВІВ
6. II.3. Основні способи і прийоми досягнення адекватності
7. III. Основні обов'язки робітників та службовців
8. IV. Основні обов'язки адміністрації
9. Overall Reflection Properties - Загальні Властивості Віддзеркалення
10. OПТИЧНІ ВЛАСТИВОСТІ КОЛОЇДНИХ СИСТЕМ
11. V. ОСНОВНІ ВИМОГИ ДО ОФОРМЛЕННЯ КУРСОВОЇ РОБОТИ
12. VII. ОСНОВНІ ЕТАПИ РОЗВИТКУ УКРАЇНСЬКОЇ КУЛЬТУРИ У ХХ ст.

Переглядів: 3547