• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тема 1:Складання математичної моделі об’єкта керування

Технічний коледж

АК -

Методичні вказівки до виконання

Практичних робіт

з дисципліни «Теорія автоматичного керування та автоматичні регулятори»

для студентів ІІ та ІІІ-го курсу, спеціальності5.092503

“Монтаж, обслуговування засобів і систем автоматизації

технологічного виробництва”

Рекомендовано до друку

методичною радою

Технічного коледжу

Протокол № від 2007

Рівне 2007

Методичні вказівки до виконання практичних робіт

з дисципліни “Теорія автоматичного керування та автоматичні регулятори” для студентів ІІ та ІІІ-го курсу, спеціальності 5.092503 “Монтаж, обслуговування засобів і систем автоматизації технологічного виробництва”

Кухнюк Н.В., - Рівне: Технічний коледж НУВГП, 2007 – 46с.

Упорядник – Кухнюк Н.В., викладач Технічного коледжу.

Відповідальний за випуск: заступник директора з навчально-методичної

роботи Тихонов Г.М.

ВСТУП

Навчальною програмою курсу “Теорія автоматичного керування та автоматичні регулятори” передбачено розв’язок практичних задач.

Сучасний етап розвитку автоматики характеризується значним ускладненням задач теорії автоматичного керування у зв’язку з переходом від автоматизації окремих об’єктів до комплексної автоматизації виробничих процесів, від керування окремими об’єктами до одночасного керування великою кількістю взаємопов’язаних об’єктів.

Дані методичні вказівки допоможуть студентам закріпити теоретичні і знання, набуті на лекціях, переконатись в умінні самостійно робити аналіз у вивченні теорії автоматичного керування. Закріпити знання загальних понять щодо елементів автоматичних систем та їх динамічних характеристик, також структури автоматичних систем, методів визначення їх динамічних характеристик, а також методів аналізу та синтезу автоматичних систем.

Тема 1:Складання математичної моделі об’єкта керування

Теоретичні відомості

Для розрахунку систем автоматичного керування технологічними

процесами чи промисловими об’єктами необхідно знати математичну модель

об’єкта керування, керуючого пристрою та інших елементів системи, які прийнято називати ланками системи. Математичний опис (математична модель ланки) складається з диференціальних та алгебраїчних рівнянь, що

встановлюють зв’язок між вхідними і вихідними сигналами. При цьому

алгебраїчні рівняння описують усталений стан системи або окремої ланки,

коли всі похідні від вхідних і вихідних сигналів рівні нулю. Ці рівнянн

називають рівняннями статики.

Диференціальні рівняння характеризують поведінку системи у часі і

Називаються рівняннями динаміки. Для отримання динамічних характеристик застосовують різні аналітичні та експериментальні методи. Аналітичні методи ґрунтуються на законах фізики, хімії, електротехніки та інших.

В найпростішому випадку, при зосередженості параметрів ланок, стаціонарності їх динамічних властивостей у часі та лінійності при малих змінах вхідних дій динамічні властивості ланки (системи) описуються лінійними диференціальними рівняннями з постійними коефіцієнтами

де x і y – відповідно вхідна і вихідна величини, a і b – коефіцієнти.

Для опису властивостей ланок більш зручно користуватися не диференціальними рівняннями, а перерахованими нижче функціями і характеристиками, що безпосередньо випливають з диференціального рівняння:

передаточною функцією );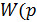

перехідною характеристикою ;

частотними характеристиками .

Для визначення передаточної і перехідної функцій ланки найбільше доцільно використовувати перетворення Лапласа, що ґрунтується на формулах прямого перетворення Лапласа:

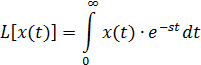
і зворотного перетворення Лапласа:

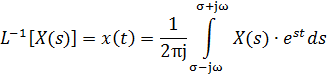
Тут під S мається на увазі комплексна змінна 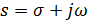. При 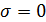перетворення Лапласа переходить в його окремий випадок – перетворення Фур’є.

Передаточною функцієюлінійної ланки називається відношення зображення Лапласа вихідної величини 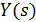до зображення вхідної величини 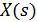при нульових початкових умовах:

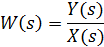
Розв’язок лінійних диференціальних рівнянь може бкти спрощений при використанні методів, що базуються на перетворенні функцій дійсної змінної у функції комплексної змінної. В операторній формі диференціальне рівняння приймає вигляд:

Знайшовши відношення зображень, отримуємо вираз для передаточної функції:

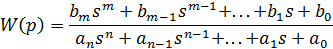
З виразу для передаточної функції видно, що вона є відношенням двох поліномів по s з коефіцієнтами, що відповідають коефіцієнтам диференціального рівняння. Таким чином встановлюється однозначний зв’язок між передаточною функцією та диференціальним рівнянням.

Задача №1. Скласти математичну модель (диференціальне рівняння) об’єкта керування у вигляді гідравлічного резервуара з постійним витоком рідини. За вхідну величину взяти зміну витрати на вході резервуара 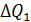, за вихідну величину прийняти зміну рівня рідини в резервуарі 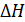. Параметри резервуара відомі.

H

1. Якщо режим установлений:

; .

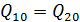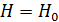2. При зміні витрати на вході:

Застосуємо закон матеріального балансу: за проміжок часу 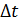об’єм в резервуарі зміниться на величину 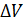(кількість речовини що поступить в резервуар):

з іншого боку зміна витрати призводить до зміни рівня:

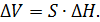
Отже, рівняння матеріального балансу прийме вигляд:

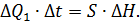
Для безмежно малого проміжку часу рівняння матеріально балансу має вигляд:

Розділимо на :

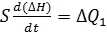- диференціальне рівняння яке описує зміну рідини в резервуарі.

Звідки:

Для 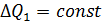використовуємо рівняння: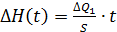

Для операторної форми запису рівняння використаємо формули переходу (прямого перетворення Лапласа):

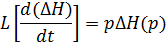
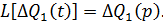
Маємо: 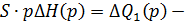операторна форма запису диф. рівняння.

Отже, передаточна функція рівна: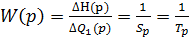

Диференціальне рівняння є математичною моделлю об’єкта керування:

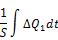
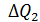
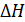
Задача №2. Скласти математичну модель об’єкта керування у вигляді резервуара з вільним витоком рідини. За вхідну величину взяти зміну витрати на вході резервуара 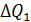, за вихідну величину прийняти зміну рівня рідини в резервуарі 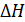. Параметри резервуара відомі. Площа резервуару рівна – S, площа отвору – w.

Початкові умови:

При зміні витрати на вході: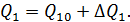

H

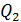
За проміжок часу dt об’єм в резервуарі зміниться на величину dV:

;

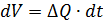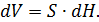
Запишемо рівняння матеріального балансу:

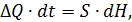
де

Витрата для отвору довільної форми рівна: .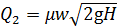

Підставимо в рівняння матеріального балансу, маємо:

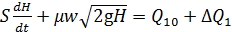– нелінійне дифрівняння 1-го порядку з постійними коефіцієнтами.

Проведемо аналітичну лінеаризацію шляхом розкладу в ряд Тейлора:

;

;

;

;

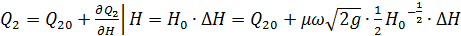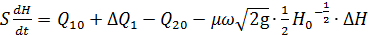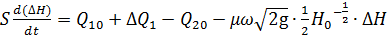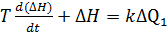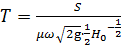– постійна часу.

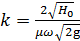– коефіцієнт передачі.

В операторній формі

.

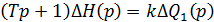Передаточна функція об’єкта керування

.

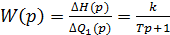де T – постійна часу,

k – коефіцієнт передачі

Задача №3. Скласти математичну модель ланки САК у вигляді електричного кола, яке складається з послідовно з’єднаних резистора і індуктивності. За вхідну величину прийняти вхідну напругуU, за вихідну – струм і.

На практиці такими елементами є обмотки збудження електричних машин постійного струму, котушки електромагнітів, елементи соленоїдних електроприводів тощо.

Отже, нам необхідно встановити залежність у динаміці вхід – вихід 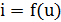використовуючи відомі положення фізики та електротехніки.

R I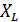

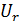
U

z

U L

Рис. 1 Схема електричного RL-кола

Тобто, ланка z являє собою два послідовно з’єднаних електричних опори – активний R і індуктивний .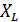

Миттєвий спад напруги на активному і індуктивному опорах відповідно позначається 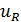і 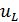. При послідовному з’єднанні опорів сума дорівнює миттєвому значенню напруги мережі: .

Враховуючи, що а ,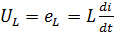

де 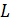– коефіцієнт самоіндукції.

Маємо: 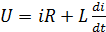- ЕРС самоіндукції.

Поділимо ліву і праву частини на R і переносимо вихідні величини в ліву частину рівняння:

,

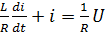де – стала часу, 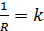- передаточний коефіцієнт ланки.

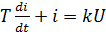– маємо рівняння динаміки ланки активно-

індуктивного опору.

В операторній формі:

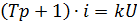
Задача №4. Скласти математичну модель ланки САК у вигляді електричного кола, яка складається з послідовно з’єднаних резистора і індуктивності. За вхідну величину прийняти вхідну напругу, за вихідну – напругу на виході.

Для отримання диференціального рівняння елемента САК складають диференціальні рівняння для вхідного параметра елемента. Стосовно електричного кола маємо:

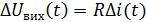
L i(t) L

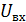R

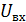
i

а б

Рис. 2.Електричне RL – коло: а – 1 схема; б – нелінійна залежність магнітної індукції L від струму i.

Допустимо, що вхідний параметр з будь-яких причин відхилився від усталеного значення 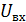на величину .

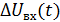Зміна напруги на вході електричного кола (рис.1) приводять до зміни струму, що протікає по колу, а отож і напруги на виході

де 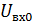, , 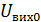- значення в усталеному режимі.

Підставимо рівняння з системи в попередні рівняння:

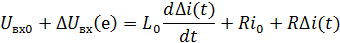
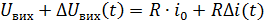
Враховуючи, що отримаємо:

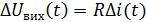
Сумісний розв’язок дає:

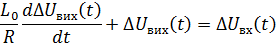
Прийнято вводити змінну 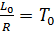- стала часу.

Лінеаризоване диференціальне рівняння в приростах матиме вигляд:

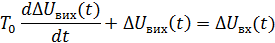
Читайте також:

1. CMM. Визначення моделі зрілості.
2. D-тригер з динамічним керуванням
3. III. GPSS — програма імітаційної моделі ЕОМ
4. III. Процедура встановлення категорій об’єктам туристичної інфраструктури
5. ISO 15504.Структура еталонної моделі
6. IV Етап: Вибір стратегії керування виявленими ризиками й виділення пріоритетних напрямків роботи
7. Аварії (катастрофи) на хімічно небезпечних об’єктах
8. Аварії на пожежно-вибухонебезпечних об’єктах
9. Аварії на радіаційно небезпечних об’єктах.
10. Аварії на радіаційно-небезпечних об’єктах
11. Аварії на хімічно небезпечних об’єктах.
12. Аварії на хімічно-небезпечних об’єктах та характеристика зон хімічного зараження.

Переглядів: 1217