• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тема 2: Типові ланки систем автоматичного керування

Теоретичні відомості

Кожна САР є динамічною системою. Автоматичний регулятор, який входить в систему регулювання, складається з багатьох функціональних елементів (вимірювального, підсилювального, виконавчого, тощо), які перетворюють одні фізичні величини і інші. Фізична величина, котра спричинює зміну іншої фізичної величини у ланці, називається вхідною (Хвх). У свою чергу фізична величина, яка є наслідком зміни першої, називається вихідною (Хвих).

Для всестороннього вивчення систем автоматики, а особливо для аналізу їх динамічних властивостей, знання лише функціональних характеристик їх складових частин недостатньо. З цієї точки зору важливішим є виявлення характеру протікання перехідного процесу при одинакових збуреннях, тобто наявність диференціальних рівнянь, які описують цей перехідний процес. Тому для аналізу динамічних властивостей САР сам об’єкт регулювання та функціональні елементи, що утворюють автоматичний регулятор, зображують у вигляді структурного об’єднання типових динамічних ланок, властивості яких та їх можливості наперед добре відомі.

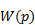
Рис.1. Загальне позначення динамічної ланки САР

Типовою динамічною ланкою називається елемент системи, чий перехідний процес описується лінійним диференціальним рівнянням не вище другого порядку. Кожна ланка зображується на схемах у вигляді чотирикутника, з однієї сторони котрого стрілкою вказується напрям вхідної величини, а з другої – вихідної. Посередині прямокутника вписується вираз його передавальної функції або математичне рівняння, що описує його перехідний процес.

Якщо врахувати, що для лінійних САР кількість типових динамічних ланок є невеликою (пропорційна, інтегруюча, диференціюючи, аперіодична,

коливальна та запізнювальна), то будь-яку систему регулювання можна розглядати як сукупність типових динамічних ланок, з’єднаних відповідним

чином. При цьому треба враховувати одну властивість: кожна ланка діє лише в одному напрямі, тобто вона не здійснює зворотного впливу на попередню ланку.

Значення передаточних функцій типових ланок:

пропорційної – ;

інтегруючої – ;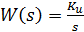

диференціюючої – ;

аперіодичної – ;

коливної – .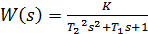

Перехідною характеристикою ланки (системи) називають її реакцію на одиничну ступінчасту дію. Вона показує, як змінюється вихідна величина ланки, коли вхідна величина є одиничною ступінчастою функцією.

Математично одинична ступінчаста функція задається виразом:

Зображення Лапласа одиничної ступінчастої функції:

Тому зображення перехідної характеристики:

Переходячи від зображення до оригіналу, знаходимо вираз для перехідної характеристики: .

Цей вираз підкреслює наявність зв’язку між перехідною характеристикою і передаточною функцією ланки.

Таким чином за перехідною характеристикою системи можна оцінити її динамічні властивості. У випадку, коли перехідну характеристику визначено експериментальним шляхом на її основи можуть бути встановлені параметри ланки.

Разом з тим, знаючи реакцію лінійної системи на ступінчасту дію, можна розрахувати реакцію на довільну дію, використовуючи інтеграл згортки:

Задача №1. Визначити аналітичний вираз перехідної функції аперіодичної ланки 1-го порядку.

За класичним методом розв’язок лінійного диференціального рівняння – є сума часткового та загального рішення:

.

Часткове рішення визначається з рівняння:

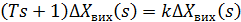, де T - стала часу.

Якщо підставити: 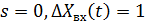. Отож .

Для диф.рівняння першого порядку:

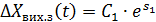
де – стала; – корінь характеристичного рівняння ; .

.

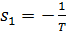Тоді:

Стала визначається з нульових початкових умов:

при , ; .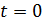

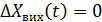Аналітичний вираз перехідної функції запишеться наступним чином:

.

Як бачимо, перехідна функція змінюється за експоненційним законом, або періодичним. Ця ланка відображає інерційність процесу, тому іноді вона називається інерційною ланкою. Перехідний процес закінчується при t=

(3-4) T, із зменшенням сталої часу T ланка простує до без інерційної ланки.

При t=T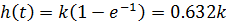

h

k

0.63k

0 T t

Рис. 3 Перехідна характеристика

Задача №2. Записати диференціальне рівняння ланки з передаточною функцією:

За означенням: ,

Маємо: .

.

Використаємо обернене зображення Лапласа (формули переходу від комплексної змінної до оригіналу):

.

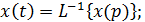
Отже, отримаємо:

.

Задача №3. Знайти передаточну функцію, якщо диференціальне рівняння має вигляд:

.

За означенням: ;

Використаємо формули переходу від оригіналу до комплексної змінної:

; .

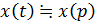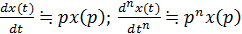Отримаємо диф. рівняння в операторній формі:

Звідки передаточна функція:

.

Задача №4. За теоремою розкладу знайти перехідну характеристику замкнутої САК, з такою передаточною функцією:

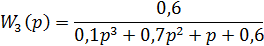
X Y

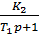
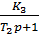
Рис. 4 Структурна схема

;

p(0.1 )=0;

p=0; 0,1 =0;

;

;

; ;

; ;

;

;

;

;

;

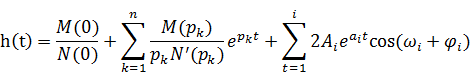
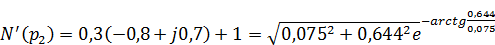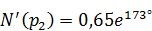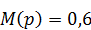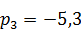a) ;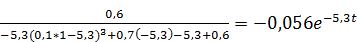

б) ;

;

;

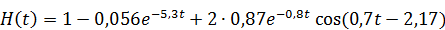При

При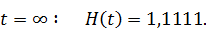

Читайте також:

1. Active-HDL як сучасна система автоматизованого проектування ВІС.
2. BANKING SYSTEM. Банковская система
3. D – моделювання в графічній системі КОМПАС
4. D-тригер з динамічним керуванням
5. D. СОЦИОИДЕОЛОГИЧЕСКАЯ СИСТЕМА ВЕЩЕЙ И ПОТРЕБЛЕНИЯ
6. Demo 7: Модель OSI (модель взаімодії відкритих систем)
7. I. Органи і системи, що забезпечують функцію виділення
8. I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
9. II. Анатомічний склад лімфатичної системи
10. II. Бреттон-Вудська система (створена в 1944 р.)
11. II. Найважливіші проблеми, що визначають розвиток місцевого самоврядування і є спільними для будь-яких урядових систем.
12. III етап. Системний підхід

Переглядів: 4875