
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Тема: Визначення статичних характеристик елементів автоматичних систем керування
Передавальні властивості елементів і систем в статичному режимі описують за допомогою статичних характеристик. Статичною характеристикою елемента називають залежність його вхідної величини Y від вхідної х
Y= f (x) = Y(x) (1.1)
в установленому статичному режимі.
Статична характеристика конкретного елемента може бути задана в формувальному вигляді (наприклад, у вигляді алгебраїчної функції y=cx2 ) або у вигляді графіка.
У загальному випадку, коли стан елемента або системи залежить від декількох вхідних впливів Х1, Х2 ... Хm, то статична характеристика представляє собою функцію декількох незалежних змінних
Y = f (Х1, Х2 ... Хm). (1.2)
Так, як статичний режим є частковою формою динамічного режиму, то відповідна статична характеристика може бути отримана як частковий вид диференційного рівняння:
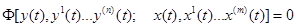 ; (1.3)
; (1.3)
Таке рівняння називають рівнянням динаміки елемента або системи. Якщо x(t) і y(t) та їх похідні входять у рівняння у вигляді добутків, степеней або часток, то ці рівняння називають нелінійними.
У випадку, коли розглядаються статичні характеристики об’єкта, зовнішні збурюючі і керуючі впливи приймаються постійними.
Якщо вивчаються динамічні властивості, то ці впливи вивчаються як змінні у часі (при цьому отримують кілька алгебраїчних і диференційних рівнянь).
Для систем керування, які описуються рівняннями з постійними параметрами, справедливий принцип накладання або суперпозиції:
Зміна вихідної величини Y(t), яка виникає при дії на систему декількох вхідних сигналів xi(t), дорівнює сумі змін Yi(t) величини Y(t), викликаних кожним сигналом окремо.
Статичні або позиційні об’єкти – об’єкти автоматичних систем, конструктивні елементи яких, в статичному режимі мають однозначні залежності між вихідною і вхідною величинами.
Деякі елементи та системи не володіють певними передавальними властивостями в статичному режимі: при різних значеннях вхідної величини х, величина у може приймати одне і те ж значення і, навпаки, при одному і тому ж значенні х, величина у може приймати будь-які значення. Такі елементи називаються астатичними. До них відносяться, наприклад, інтегруючі ланки.
По виду статичних характеристик елементи поділяють на лінійні і нелінійні. Статична характеристика лінійного елемента описується лінійною функцією y=b+ax. У нелінійних елементів зв’язок між вхідною і вихідною величиною виражається звичайно у вигляді степеневих функцій, степеневих поліномів, дробових раціональних функцій і більш складних функцій.
Нелінійні елементи в свою чергу поділяють на елементи з істотно-нелінійною статичною характеристикою і елементи з несуттєво нелінійною характеристикою. Останні можна лінеаризувати.
Статична характеристика є несуттєво нелінійною, якщо вона описується неперервно-диференційованою функцією.
Лінеаризацією називається наближена зміна нелінійної функції лінійною. Лінеаризація нелінійної характеристики є вірною, якщо в процесі роботи елемента його вхідна величина змінюється в невеликому діапазоні навколо деякого значення х=х0. Статична характеристика вважається суттєво нелінійною, якщо вона має злами або розриви.
Лінеаризацію гладких статичних характеристик можна здійснювати або по методу дотичної, або по методу січної.
Коефіцієнт пропорційності К між відхиленнями вихідної і вхідної величини в статичному режимі називають передавальним коефіцієнтом.
Передавальний коефіцієнт є основним параметром лінійних і лінеаризованих елементів статичного типу: його числове значення цілком характеризує передавальні властивості елемента в статиці.
Розмірність передавального коефіцієнта рівна відношенню розмірності вихідної величини до розмірності вхідної величини:
[k]=[y]/[x]
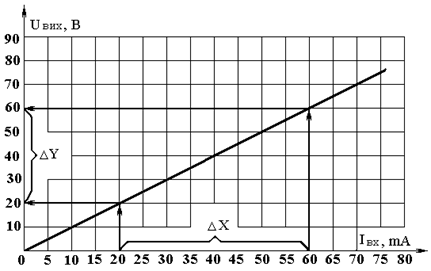
Передавальний коефіцієнт обчислюється за формулою:
 ,
,
де Dу, Dх – відхилення вихідної і вхідної величин відповідно.
Практичне заняття №2
Властивості та характеристики
одноємнісних об'єктів та складання диференційних рівнянь
Одноємнісний, або одномірний керований об'єкт ОКО, характеризується двома узагальнюючими координатами 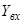 ,
,  (рис. 2.1).
(рис. 2.1).
 Рисунок 2.1 – Модель “вхід – вихід” одноємнісного об'єкта
Рисунок 2.1 – Модель “вхід – вихід” одноємнісного об'єкта
|
Вхідна величина 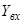 – це величина енергетичного або матеріального потоку, що поступає на вхід об'єкта (
– це величина енергетичного або матеріального потоку, що поступає на вхід об'єкта ( 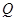 ).
).
Вихідна величина  – це стан об'єкта (
– це стан об'єкта ( 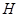 ) або координати, зв'язаних між собою рівнянням балансу енергії або речовини, що накопичуються в об'єкті
) або координати, зв'язаних між собою рівнянням балансу енергії або речовини, що накопичуються в об'єкті
 . (2.1)
. (2.1)
Це основне рівняння одноємнісного об'єкта.
Тут: 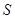 – постійна величина, що характеризує акумулюючу властивість об'єкта;
– постійна величина, що характеризує акумулюючу властивість об'єкта; 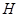 – показник стану об'єкта;
– показник стану об'єкта; 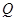 – кількість енергії або речовини, що поступає в об'єкт за одиницю часу (дорівнює різниці притоку
– кількість енергії або речовини, що поступає в об'єкт за одиницю часу (дорівнює різниці притоку 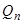 і стоку
і стоку  енергії або речовини)
енергії або речовини)
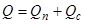 . (2.2)
. (2.2)
Одна з величин, яка входить в рівняння (2.2), є збурюючим впливом або навантаженням, тоді друга величина використовується, як керуючий вплив.
Якщо  , то
, то 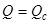 . Тоді
. Тоді 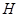 – незмінна.
– незмінна.
При всякому 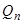 і
і  величина
величина 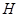 згідно з рівнянням (2.1) буде зростати або зменшуватись залежно від знаку
згідно з рівнянням (2.1) буде зростати або зменшуватись залежно від знаку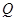 .
.
Величина 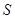 називаєтьсякоефіцієнтом ємності і визначає швидкість зміни координати
називаєтьсякоефіцієнтом ємності і визначає швидкість зміни координати 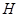 при постійному значенні показника
при постійному значенні показника 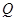 .
.
Якщо об'єкт являє собою резервуар, в який поступає рідина, то координата 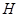 є рівнем рідини. Показник
є рівнем рідини. Показник 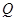 – різниця між припливом і стоком рідини за одиницю часу. Площа поверхні рідини є коефіцієнтом ємності
– різниця між припливом і стоком рідини за одиницю часу. Площа поверхні рідини є коефіцієнтом ємності 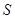 .
.
Чим більша ця площа, тим повільніше проходить зміна рівня при одній і тій же різниці між припливом і стоком.
Коефіцієнт ємності 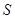 може бути постійним або змінним. Наприклад, для резервуара у вигляді циліндра
може бути постійним або змінним. Наприклад, для резервуара у вигляді циліндра 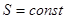 при будь-якому значенні рівня
при будь-якому значенні рівня 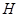 . Якщо резервуар має форму конуса, то буде залежати від поточного значення
. Якщо резервуар має форму конуса, то буде залежати від поточного значення 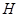 , а рівняння стане нелінійним. В об'єктах з постійним коефіцієнтом ємності
, а рівняння стане нелінійним. В об'єктах з постійним коефіцієнтом ємності 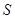 кожному значенню показника
кожному значенню показника 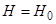 відповідає визначена кількість енергії або речовини, акумульованої ємністю об'єкта
відповідає визначена кількість енергії або речовини, акумульованої ємністю об'єкта
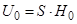 . (2.3)
. (2.3)
В одному і тому ж технічному апараті можуть відбуватися декілька процесів різної фізичної природи.
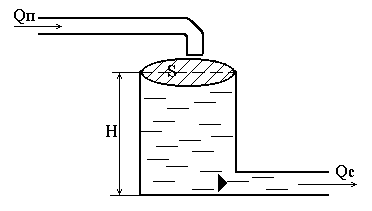 Рисунок 2.2 – Одноємнісний об'єкт
Рисунок 2.2 – Одноємнісний об'єкт
|
Приклад.Нагрівання і вихід вологи відбуваються одночасно при сушці. Такий технічний процес і апарат характеризується декількома коефіцієнтами ємності. Якщо в середині технічного апарата можна виділити декілька ділянок, що мають 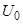 , і якщо перехід енергії або речовини від однієї ділянки до другої затруднений, то такий апарат – багатоємнісний об'єкт.
, і якщо перехід енергії або речовини від однієї ділянки до другої затруднений, то такий апарат – багатоємнісний об'єкт.
Таблиця 2.1 — Приклади одноємнісних об'єктів
| Процес | Вихідна величина, H | Вхідна величина, Q | Коефіцієнт ємності, S |
| Поступальний рух тіла | Лінійна швид-кість, м/с | Результуюча сила, Н | Маса, кг |
| Обертальний рух тіла | Кутова швид-кість, рад/с | Результуючий момент, Нм | Момент інер-ції, кгм2 |
| Заповнення ре-зервуара газом | Тиск, н/м2 | Масова витяга газу, кг/с | Об’єм резер-вуара: газова постійна ´ аб-солютну тем-пературу, с2 |
| Нагрівання або охолодження | Температура тіла, °С | Тепловий потік, Дж | Теплоємність тіла, Дж/°С |
| Сушка або зволоження | Відносна во-логість | Маса вологи, яка виходить за оди-ницю часу, кг/с | Маса сухої речовини, кг |
| Розчинення | Концентрація речовини, кг/м3 | Поступлення су-хої речовини за одиницю часу, кг/с | Ємність апара-та, м3 |
Кожну ділянку в цьому випадку потрібно розглянути окремо, як одноємнісний об'єкт. Крім цього основного рівняння (2.2), одноємнісний об'єкт підпорядковується закону, згідно з яким відбувається обмін енергії і речовини між об'єктом і зовнішнім середовищем. В узагальнюючій формі цей закон може бути виражений у вигляді 2-х залежностей
 . (2.4)
. (2.4)
Ці залежності мають нелінійний характер (рис. 2.4).
При аналізі такі залежності необхідно лінеаризувати. Поведінка об'єктів в часі залежить від співвідношення похідних  і
і 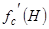 в точці, яка відповідає режиму, що розглядається.
в точці, яка відповідає режиму, що розглядається.
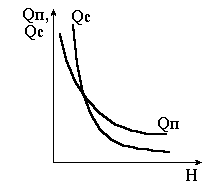 Рисунок 2.3 – Нелінійні залежності
Рисунок 2.3 – Нелінійні залежності 
|
Наприклад:Якщо в резервуарі з рідиною при рівні  різниця похідних
різниця похідних
 , (2.5)
, (2.5)
то випадково виникла різниця між припливом і стоком буде зменшуватись в міру збільшення 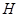 . Через деякий час вона буде 0, а рівень стане постійним
. Через деякий час вона буде 0, а рівень стане постійним 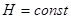 . В цьому випадку говорять, що об'єкт має властивістьсамовирівнювання.
. В цьому випадку говорять, що об'єкт має властивістьсамовирівнювання.
Якщо різниця (2.5) буде менша 0, то із збільшенням рівня буде збільшуватись різниця між припливом і стоком, що в свою чергу викличе подальше зростання рівня. Це означає, що самовирівнювання в об'єкті відсутнє.
Самовирівнювання – це властивість об'єкта, завдяки якій невідповідність між припливом і стоком енергії речовини самостійно прямує до 0, а вихідна величина прямує до нового встановленого значення. Все проходить без керування.
Складемо загальне диференціальне рівняння одноємнісного об'єкта, враховуючи умови балансу і закони обміну,
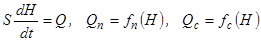 .
.
Для прикладу візьмемо резервуар з рідиною. Нехай до подачі зовнішнього впливу об'єкт перебуває в статичному режимі, коли приплив і стік однакові 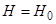 . Після ступінчастої зміни припливу рідини на величину
. Після ступінчастої зміни припливу рідини на величину  відбувається зміна рівня рідини
відбувається зміна рівня рідини 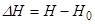 . Зміна рівня зумовлює збільшення або зменшення припливу і стоку. Знайдемо нові значення припливу і стоку. Для цього розкладемо залежність в ряд Тейлора
. Зміна рівня зумовлює збільшення або зменшення припливу і стоку. Знайдемо нові значення припливу і стоку. Для цього розкладемо залежність в ряд Тейлора
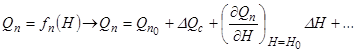
і (2.6)

Враховуючи, що  , підставимо ці значення в рівняння (2.1)
, підставимо ці значення в рівняння (2.1)
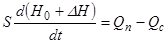 .
.
Дане рівняння можна спростити враховуючи, що у вихідному стані приплив і стік були рівні, а також що похідна від  , яка є постійна, дорівнює 0.
, яка є постійна, дорівнює 0.
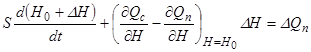 . (2.7)
. (2.7)
Диференціальне рівняння (2.7) об'єкта зв'язує змінну в часі величину 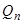 і вихідну величину
і вихідну величину 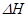 . Дане рівняння складалось з використанням лінеаризації, і тому воно дійсне лише для малих відхилень величин
. Дане рівняння складалось з використанням лінеаризації, і тому воно дійсне лише для малих відхилень величин 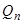 і рівня
і рівня 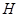 від значень
від значень 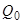 і
і  . Дане рівняння можна переписати у відносних одиницях і ввести поняття коефіцієнта самовирівнювання. Для цього використовуються базові значення статичного режиму. В даному випадку вигідно прийняти за базові
. Дане рівняння можна переписати у відносних одиницях і ввести поняття коефіцієнта самовирівнювання. Для цього використовуються базові значення статичного режиму. В даному випадку вигідно прийняти за базові 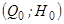 ;
;
 ,
,
тоді  .
.
Якщо підставити ці значення в рівняння (2.7), то отримаємо
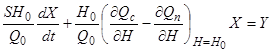 . (2.8)
. (2.8)
Коефіцієнт, що стоїть перед  , позначають через
, позначають через 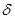
 .
.
Коефіцієнт 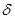 називається коефіцієнтом самовирівнювання.
називається коефіцієнтом самовирівнювання.
Величина і знак коефіцієнта 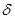 залежать від відношення похідних. Якщо розділити ліву і праву частини рівняння на абсолютне значення коефіцієнта
залежать від відношення похідних. Якщо розділити ліву і праву частини рівняння на абсолютне значення коефіцієнта 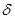 , то це рівняння можна привести до стандартної форми
, то це рівняння можна привести до стандартної форми
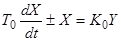 . (2.9)
. (2.9)
Тут  — постійна часу об'єкт;
— постійна часу об'єкт;  — безрозмірний передавальний коефіцієнт об'єкта.
— безрозмірний передавальний коефіцієнт об'єкта.
Якщо 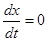 , то рівняння (2.9) перетворюється в рівняння
, то рівняння (2.9) перетворюється в рівняння 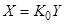 ,яке описує статичні властивості об'єкта. З цих виразів випливає, що чим більше
,яке описує статичні властивості об'єкта. З цих виразів випливає, що чим більше 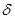 , тим менша постійна часу і передавальний коефіцієнт об'єкта.
, тим менша постійна часу і передавальний коефіцієнт об'єкта.
1. Якщо 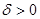 , то одноємнісний об'єкт має властивість самовирівнювання і за своїми динамічними властивостями еквівалентний стійкій інерційній ланці 1-го порядку.
, то одноємнісний об'єкт має властивість самовирівнювання і за своїми динамічними властивостями еквівалентний стійкій інерційній ланці 1-го порядку.
2. Якщо  , то самовирівнювання відсутнє, і такий об'єкт еквівалентний ідеальній інтегруючій ланці.
, то самовирівнювання відсутнє, і такий об'єкт еквівалентний ідеальній інтегруючій ланці.
3. Якщо 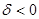 , то в рівнянні (2.9) перед змінною Х буде “–“, що відповідає додатному кореню зростаючої перехідної функції.
, то в рівнянні (2.9) перед змінною Х буде “–“, що відповідає додатному кореню зростаючої перехідної функції.
На рис. 2.4, 1 зображений резервуар, в якому приплив не залежить від рівня рідини 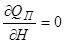 . Ця ж умова витримується для рис. 2.4, 2, 3. Але ж умова стоку рідини у всіх випадках різна. В резервуарі рідина тече вільно через вихідний патрубок. Залежність стоку від рівня при будь-яких значеннях рівня має додатний нахил. Чим більший рівень
. Ця ж умова витримується для рис. 2.4, 2, 3. Але ж умова стоку рідини у всіх випадках різна. В резервуарі рідина тече вільно через вихідний патрубок. Залежність стоку від рівня при будь-яких значеннях рівня має додатний нахил. Чим більший рівень 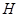 тим більша величина стоку
тим більша величина стоку  . Коефіцієнт самовирівнювання
. Коефіцієнт самовирівнювання 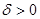 і після зовнішнього впливу у вигляді збільшення припливу рівень прямує до нового встановленого значення.
і після зовнішнього впливу у вигляді збільшення припливу рівень прямує до нового встановленого значення.
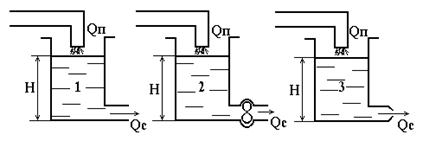 Рисунок 2.4 – Приклади одноємнісних об'єктів
Рисунок 2.4 – Приклади одноємнісних об'єктів
|
 Рисунок 2.5 – Перехідні характеристики об'єктів, приведених на рис. 2.4
Рисунок 2.5 – Перехідні характеристики об'єктів, приведених на рис. 2.4
|
У 2-ому резервуарі стік рідини відбувається вимушено за допомогою насоса. Це означає, що стік  не залежить від рівня рідини
не залежить від рівня рідини 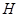 і
і  . В цьому випадку рівень рідини збільшується незалежно від величини потоку.
. В цьому випадку рівень рідини збільшується незалежно від величини потоку.
У 3-ому резервуарі зворотний клапан в міру збільшення рівня рідини зменшує стік 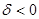 , рівень рідини збільшується зі зростаючою швидкістю.
, рівень рідини збільшується зі зростаючою швидкістю.
Практичне заняття №3
Читайте також:
- A) Оцінка захисних споруд за ємністю – визначення коефіцієнта Квм.
- Active-HDL як сучасна система автоматизованого проектування ВІС.
- BANKING SYSTEM. Банковская система
- CMM. Визначення моделі зрілості.
- D – моделювання в графічній системі КОМПАС
- D-тригер з динамічним керуванням
- D. СОЦИОИДЕОЛОГИЧЕСКАЯ СИСТЕМА ВЕЩЕЙ И ПОТРЕБЛЕНИЯ
- Demo 7: Модель OSI (модель взаімодії відкритих систем)
- I визначення впливу окремих факторів
- I. Загальна характеристика політичної та правової думки античної Греції.
- I. Органи і системи, що забезпечують функцію виділення
- I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
| <== попередня сторінка | | | наступна сторінка ==> |
| Система оцінки знань | | | Тема: Перехідні і амплітудно-фазові характеристики (АФХ) ланок автоматичних систем керування (АСК) |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |