Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Тема: Перехідні і амплітудно-фазові характеристики (АФХ) ланок автоматичних систем керування (АСК)

Найбільш наочне уявлення продинамічні властивості елемента дає йогоперехідна функція.

Перехідною функцією називається зміна вихідної величини в часі після подачі на вхід одиничного ступінчатого впливу при нульових початкових умовах.

Перехідна функція задається графічно або формулою.

Рисунок 3.1 – Графічне зображення перехідної функції

Формульний вираз перехідної функції можна одержати, якщо розв'язати диференційне рівняння при

, (3.1)

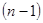Ці умови означають, що вихідна величина і її похідні до -го порядку безпосередньо перед подачею вхідного впливу рівні 0.

Перехідна функція має дві складові: вимушену 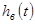і вільну : .

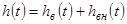Вимушена складова дає частковий розв'язок рівняння при ступінчатому впливі. Вона дорівнює усталеному значенню вихідної величини при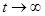

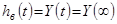. (3.2)

Вільна складова, знаходиться з розв'язку однорідного диференційного рівняння

, (3.3)

де – корені характеристичного рівняння, – сталі інте-
грування, які залежать від початкових умов.

Для лінійних систем, крім принципу суперпозиції, справедливе загальне правило:

Реакція на неодиничний ступінчатий вплив дорівнює добутку перехідної функції на коефіцієнт а:

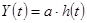Часто процеси, що проходять в окремих ланках системи недостатньо вивчені і оддержати вихідні рівняння для них важко. В таких випадках доцільно використовувати частотні характеристики.Їх можна не лише побудувати за лінеаризованими рівняннями окремих елементів але й знайти експериментально.

Частотні характеристики дають можливість вивчити реакції системи на гармонічні впливи.

Величина амплітуди вихідного сигналу Y_m залежить від амплітуди вхідного сигналу X_m і від параметрів самої системи. Щоб виключити X_m розглядають відношення Y_m/X_m=A.

Відносне значення амплітуди А і зсуву фаз j залежать від частоти w:

A=A(w); j=j(w). (3.4)

Залежність А=А(w) – це амплітудно–частотна характеристика (АЧХ), а залежність j=j(w) – це фазово–частотна характеристика (ФЧХ). На підставі АЧХ і ФЧХ можна отримати амплітудно–фазову характеристику (АФХ) системи. Характеристика будується в комплексній площині. Вектор АФХ будується таким чином, що кут з горизонтальнлю віссю є j(w), а сам ветор – А(w). Кінець вектора А(w) при зміні від 0 до ¥ описує траекторію, яка називається амплітудно-фазовою характеристикою (АФХ). Проекція вектора АФХ на дійсну вісь називається дійсною частиною АФХ. Проекція вектора АФХ на уявну вісь називається уявною частиною АФХ.

При побудові АФХ j(w) відкладається проти годинникової стрілки, якщо його значення додатнє і за годинниковою стрілкою, якщо його значення від’ємне. Взаємозв’язок між АЧХ і ФЧХ може бути виражений наступним чином:

W(jw)=A(w)^j^j⁽^w⁾ , (3.5)

Перевагою АФХ можливість її отримання із передавальної функції шляхом заміни р→jω.

Передавальною функцією 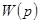лінійної стаціонарної автоматичної системи називається відношення зображення за Лапласом вихідної величини 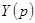до зображення за Лапласом вхідної величини 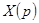при нульових початкових умовах

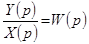, (3.6)

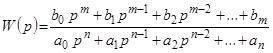. (3.7)

Висновок: Для того, щоб знайти передавальну функцію 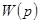лінійної стаціонарної системи, необхідно:

1. Лінійне диференціальне рівняння перетворити за Дапласом з урахуванням початкових умов.

2. Взяти відношення вихідної і вхідної величин, перетворених за Лапласом.

Наприклад: визначити 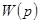лінійної стаціонарної системи, яка описується рівнянням: .

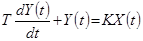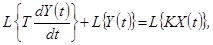
. (3.8)

Перехідну функцію можна визначити на підставі співвідношень 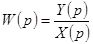і .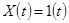

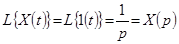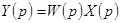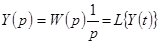. (3.9)

Таким чином, щоб знайти вираз для , необхідно взяти зворотний вираз Лапласа від : . Якщо вхідний вплив d-функція, то враховуючи, що перетворення Лапаласа від , одержимо

, (3.10)

тоді функція .

Висновок: Імпульсна перехідна функція є оригіналом передавальної функції .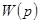

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Тема: Визначення статичних характеристик елементів автоматичних систем керування	\|	Практичне заняття №4

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.