Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

ТЕМА 4. СЕРЕДНІ ВЕЛИЧИНИ І ПОКАЗНИКИ ВАРІАЦІЇ

4.1 Сутність і значення середніх величин

4.2 Види середніх і способи їхнього розрахунку

4.3 Порядкові середні (медіана і мода)

4.4 Показники варіації і їхній розрахунок

Середні величини, поряд з методом групувань, займають чільне місце в статистиці. Вони широко застосовуються в різних галузях наукової та практичної діяльності.

Важливу роль відіграють вони і у роботі економіста:

– їх використовують в економічному аналізі господарської діяльності підприємств, організацій і фірм;

– порівнянні рівня зарплати в галузях, на підприємствах, у цехах;

– плануванні і прогнозуванні середніх витрат сировини, матеріалів, палива, енергії і т.д.

Середньою величиною в статистиці називається показник, що характеризує узагальнююче значення варіюючої ознаки одиниць, сукупності.

Головне значення середніх величин в їх узагальнюючій функції, тобто в заміні безлічі різних індивідуальних значень ознаки їх середньою величиною, що характеризує всю сукупність.

Середня є величиною абстрактною і часто може бути виражена в таких числах, яких немає в реальному житті.

НАПРИКЛАД, середній розмір родини в країні – 3,4 чол., або ж забезпеченість автомобілями – 1,2 на кожні 10 чол. і т.ін.

Засновником теорії середніх величин є вже згадуваний раніше відомий бельгійський вчений А.Кетле.

Він уперше зробив спробу з наукових позицій визначити природу середніх величин і закономірностей, що виявляються в них.

Середню величину він вважав відображенням деякої «істинної» величини, що формується під впливом вічних і незмінних сил природи.

А.Кетле довів, що масові суспільні явища підкоряються певним статистичним закономірностям, що виявляються найчастіше саме в середніх величинах. За допомогою середніх величин, вважав він, можна мати уяву про «істинні» типи явищ і закономірностях масових процесів громадського життя, що ніяк інакше пізнати неможливо.

Бажаючим більш докладно ознайомитися з теорією середніх величин Кетле можна порекомендувати його книги: «Соціальна фізика», «Соціальна система і закони, які нею управляютьі» і ін.

У практиці сучасної статистики середні величини використовуються все частіше не тільки для узагальнення якісно однорідних явищ, але і неоднорідних.

Так, середня врожайність зернових у країні узагальнює явно якісно неоднорідні культури: пшеницю з врожайністю 30 – 35 ц/га, гречку з врожайністю 6 – 10 ц/га і кукурудзу, що дає 50 – 60 ц/га. Причому, якість ґрунтів у різних регіонах країни, теж різна.

Такого роду середні величини, що узагальнюють якісно неоднорідні значення ознаки в сукупності і характеризують просторові системи (держава, регіон, галузь) або динамічні системи, що простягаються у часі (рік, десятиліття, сезон), називаютьсясистемними.

НАПРИКЛАД: середня величина національного доходу на душу населення, середня врожайність зернових у країні, середнє споживання різних продуктів на душу населення і т.ін.

Або, середня температура повітря в місті за 1995 р. дорівнює +8,7°. Вона узагальнює різнорідні температури різних пір року.

Якщо ж середня величина узагальнює якісно однорідні значення ознаки в сукупності, то вона називається типовою.

НАПРИКЛАД: середній вік студентів 1-го курсу, середній зріст студенток 20-літнього віку, середня відвідуваність лекцій по статистиці, середня витрата коштів пенсіонерів на харчування, середня річна температура повітря в місті на основі середніх багаторічних температур.

У статистиці застосовуються різні види середніх величин: середня арифметична, середня геометрична, середня гармонійна, середня квадратична, кубічна, біквадратична, прогресійна і ін. ступенів, тому що відноситься до класу ступеневих.

Кожен вид середньої має свої властивості, що відповідають вирішенню певної задачі. Тому вибір виду середньої має важливе значення і визначається, як правило, економічною сутністю ознаки, яка осереднюється.

Найбільш розповсюдженою в економічних розрахунках і соціально-економічному аналізі є середня арифметична. Середня арифметична підрозділяється на просту і зважену.

Середня арифметична проста застосовується в тих випадках, коли кожне індивідуальне значення ознаки (числовий варіант) зустрічається один раз чи однакове число разів.

Інакше кажучи, середня арифметична проста розраховується по незгрупованих одиницях сукупності.

Її розраховують шляхом підсумовування окремих одиниць і ділення отриманої суми на кількість величин.

Тобто, якщо є значення ознаки, що варіює, (його варіанти): , то середня арифметична проста обчислюється:

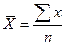НАПРИКЛАД, якщо студент за результатами сесії одержав оцінки : 5; 3; 4, то середній бал його успішності:

Середня арифметична зважена застосовується в тих випадках, коли значення ознаки в сукупності зустрічаються багато разів і неоднакове число раз. Тобто коли варіанти ознаки, що варіює, мають різні частоти. У подібних випадках ми маємо справу, як нам уже відомо, із сгрупованими даними або з варіаційними рядами розподілу.

1.Якщо ряд дискретний і частота кожного варіанта різна, то для обчислення середньої арифметичної необхідно:

а) помножити кожен варіант на його частоту;

б) знайти суму отриманих добутків варіантів на частоти;

в) знайти суму частот (якщо вона невідома);

г) суму добутків варіантів на частоти розділити на суму частот.

У загальному вигляді обчислення середньої арифметичної зваженої для дискретного ряду можна представити в таким чином:

Варіанти, (х)	Частоти, (f)	Добуток варіантів на частоти, (x×f)
х₁	f₁	х₁×f₁
х₂	f₂	х₂×f₂
…	…	…
х_n	fn	x_n×f_n

S f_i S x_i× f_i

обсяг явища

Таким чином, середня арифметична дискретного ряду обчислюється як частка від ділення суми добутків варіантів на частоти на суму частот.

Отже, щоб знайти середню арифметичну дискретного ряду необхідно здійснити наступні операції:

1. Побудувати 3-й стовпець таблиці ряду і заповнити його добутками елементів 1-го стовпця на 2-й, тобто знайти добуток варіантів на частоти.

2. Визначити суму добутків варіантів на частоти (Sxf).

3. Визначити суму частот (Sf).

4. Визначити частку від ділення суми добутків варіантів на частоти на суму частот .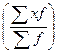

2.Якщо ряд інтервальний, то обчислення середньої арифметичної має одну особливість.

Вона полягає в тому, що в стовпці варіантів значення ознак представлені не одним числом, а певним інтервалом – нижньою і верхньою його межами.

Для того, щоб розрахувати середню арифметичну інтервального ряду необхідно:

1) визначити середню величину кожного інтервалу (його середину) як напівсуму верхньої і нижньої межі;

2) визначити середню для всього ряду в тій послідовності, що і для дискретного варіаційного ряду.

2.1Якщо інтервальний ряд має відкриті інтервали в першій і останній групі, то спочатку треба визначити невідомі границі інтервалів.

А) Вони визначаються або експертним шляхом виходячи із сутності, властивостей ознаки і сукупності;

Б) або величина інтервалу в першій групі приймається рівною інтервалу наступної групи, а величина інтервалу в останній групі дорівнює інтервалу попередньої групи.

Пояснимо це на наступних конкретних прикладах.

А) Нехай є інтервальний ряд розподілу робітників цеху за віком:

Групи робітників за віком, років (х)	Число робітників (f)	Середина інтервалу (х')
до 20		18,5 = (17+20)/2
20 – 30
30 – 40
40 – 50
старше 50		57,5 = (50+65)/2
Разом:

У першій групі відсутня нижня межа інтервалу, а в останній – верхня.

Якщо подивитися на сутність ознаки – вік, то логічно, що нижня межа не може бути менше 17 років, тому середина інтервалу буде дорівнює 18,5.

Що стосується верхньої межі останнього інтервалу, то максимальний вік робітника не може бути більшим 65 років.

Б) Нехай є наступний ряд розподілу робітників за кількістю виготовлених деталей:

Виготовлено деталей, шт. (х)	Число робітників (f)	Середнє значення інтервалу (х')
до 10		9 = (8+10)/2
10 – 12
12 – 16
16 і більш		18 = (16+20)/2
Разом:

Величину інтервалу в першій групі прийняли рівною інтервалу наступної, тобто 2. Тоді нижня межа буде дорівнює 8. Величину інтервалу в останній групі прийняли рівною величині інтервалу попередньої групи, тобто 4. Отже, верхня межа буде дорівнює 20.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Абсолютні і відносні статистичні величини	\|	Середня арифметична з відносних величин

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.