
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Багатовимірні випадкові величини. Система двох випадкових величин
На одному й тому самому просторі елементарних подій W можна визначити не одну, а кілька випадкових величин. Така потреба постає, наприклад, коли досліджуваний об’єкт характеризується кількома випадковими параметрами. Так, у разі виготовлення валів такі їх параметри, як діаметр, довжина, овальність є випадковими величинами, значення яких наперед не можна передбачити. Або, скажімо, структура витрат випадково взятої окремої сім’ї на їжу, одяг, взуття, транспорт, задоволення духовних потреб також є випадковими величинами, визначеними на одному й тому самому просторі елементарних подій.
На багатовимірні випадкові величини поширюються майже без змін основні означення, які були розглянуті для одновимірної випадкової величини.
Означення.Одночасна поява внаслідок проведення експерименту n випадкових величин (X1, X2, …, Xn) з певною ймовірністю являє собою n-вимірну випадкову величину, яку називають також системою n випадкових величин, або n-вимірним випадковим вектором.
1. Система двох дискретних випадкових величин (X, Y) та їх числові характеристики
Законом розподілу двох дискретних випадкових величин називають перелік можливих значень Y = yi , X = xj та відповідних їм імовірностей спільної появи.
У табличній формі цей закон має такий вигляд:
 X = xj
Y = yi X = xj
Y = yi
| x1 | x2 | x3 | … | xm | pyi |
| y1 | p11 | p12 | p13 | p1m | py1 | |
| y2 | p21 | p22 | p23 | p2m | py2 | |
| y3 | p31 | p32 | p33 | p3m | py3 | |
| … | … | … | … | … | … | … |
| yk | pk1 | pk2 | pk3 | … | pkm | pym |
| pxj | px1 | px2 | px3 | … | pxm |
Тут використано такі позначення
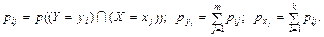
Умова нормування має такий вигляд:
 (1)
(1)
2. Основні числові характеристики для випадкових величин Х, Y, що утворюють систему (Х, Y)
 (2)
(2)

 (3)
(3)
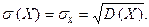 (4)
(4)
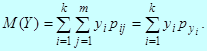 (5)
(5)

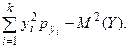 (6)
(6)
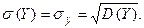 (7)
(7)
3. Кореляційний момент. Коефіцієнт кореляції та його властивості
Під час вивчення системи двох і більше випадкових величин доводиться з’ясовувати наявність зв’язку між цими величинами та його характер. З відповідною метою застосовують так званий кореляційний момент:
 (8)
(8)
У разі Κху = 0 зв’язок між величинами Х та Y, що належать системі (Х, Y), відсутній. Коли Κху ¹ 0, то між відповідними Х і Y кореляційний зв’язок існує.
Тісноту кореляційного зв’язку характеризує коефіцієнт кореляції:
 (9)
(9)
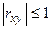 , або
, або 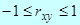 .
.
Отже, якщо випадкові величини Х та Y є незалежними, то Κху = 0 і rху = 0. Рівність нулеві rху є необхідною, але не достатньою умовою незалежності випадкових величин.
Справді, може існувати система залежних випадкових величин, в якої коефіцієнт кореляції дорівнює нулю. Прикладом такої системи є система двох випадкових величин (X, Y), яка рівномірно розподілена всередині кола радіусом R із центром у початку координат. Дві випадкові величини Х і Y називають некорельованими, якщо rху = 0, і корельованими, якщо rху ¹ 0.
Отже, якщо Х і Y незалежні, то вони будуть і некорельованими. Але з некорельованості випадкових величин у загальному випадку не випливає їх незалежність.
 Приклад 1.Задано закон розподілу системи двох дискретних випадкових величин (X, Y):
Приклад 1.Задано закон розподілу системи двох дискретних випадкових величин (X, Y):
| Х = хj Y = yi | 5,2 | 10,2 | 15,2 | Pyi |
| 2,4 | 0,1a | 2a | 0,9a | |
| 4,4 | 2a | 0,2a | 1,8a | |
| 6,4 | 1,9a | 0,8a | 0,3a | |
| Pxj |
Знайти а. Обчислити M (X); D (X); s (X); M (Y); D (Y); s (Y); Kху; rху; P (2,4 £ Y < 6,4; 5,2 < X £ 15,2).
Читайте також:
- Active-HDL як сучасна система автоматизованого проектування ВІС.
- II. Бреттон-Вудська система (створена в 1944 р.)
- IV. Система зв’язків всередині центральної нервової системи
- IV. УЗАГАЛЬНЕННЯ І СИСТЕМАТИЗАЦІЯ ВИВЧЕНОГО
- V. Систематизація і узагальнення нових знань, умінь і навичок
- VI. Система навчаючих завдань для перевірки кінцевого рівня завдань.
- VI. Система навчаючих завдань для перевірки кінцевого рівня завдань.
- VI. Узагальнення та систематизація знань
- VII. Закріплення нового матеріалу і систематизація знань.
- Абсолютна величина числа позначається символом .
- Абсолютні і відносні величини
- Абсолютні і відносні статистичні величини
| <== попередня сторінка | | | наступна сторінка ==> |
| Правочини з дефектами форми | | | Розв’язання. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |