• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Деякі варіанти моделі Рамсея

Варіант 1.У макроекономічному моделюванні особливе місце належить моделям економічного росту, історія яких починається з 30-х років минулого сторіччя. Ще в 1927 р. англійський економіст Ф. Рамсей опублікував статтю, присвячену питанням економічного росту та задачі вибору оптимального варіанта розвитку економіки. Прийнято вважати, що поставлена Рамсеєм задача є першим прикладом застосування теорії динамічної оптимізації в економіці [22]. Рамсей розглядав агреговану замкнуту економіку (тобто економіку, що виробляє єдиний однорідний продукт і в якій відсутній як імпорт в економіку, так і експорт з неї). Крім того, Рамсей вважав, що населення й трудові ресурси не залежать від змінної часу 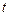, а випуск продукції 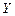може зростати лише завдяки накопиченню капіталу під впливом інвестицій , які повністю витрачаються на приріст капіталу .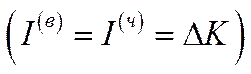

Інакше кажучи, чистий (кінцевий) випуск 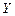описувався однофакторною ВФ

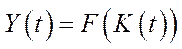. (6.21)

Змінна часу вказана неявно у зв’язку з тим, що запас капіталу залежить від часу. Стосовно змінної часу 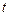зауважимо, що надалі час буде неперервним (він може вимірюватись у роках). Значення будь-якого економічного показника в момент 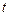природне, оскільки, наприклад, в будь-який день можна встановити кількість зайнятих і шляхом інвентаризації обсяг ОВФ. Значення показника в момент 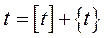можна визначити як суму відповідних накопичень за конкретний рік 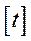та конкретну кількість днів 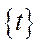(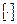– ціла частина числа,
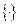– дробова частина числа).

Повернемося до опису моделі Рамсея. Як і на рис. 6.1, весь випуск 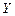витрачається на невиробниче споживання та інвестиції, тобто маємо уточнену рівність (6.2)

. (6.22)

Оскільки інвестиції, як уже було сказано, повністю вкладаються на приріст капіталу, а в моделі з неперервним часом цей приріст збігається з похідною 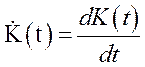, то динаміка капіталу формалізується диференціальним рівнянням

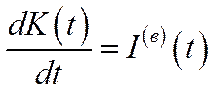(6.23)

яке обов’язково доповнюється початковою умовою (умовою Коші)

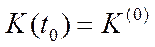(6.24)

де 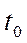– початковий момент часу, для якого обсяг капіталу 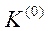відомий.

Об’єднавши співвідношення (6.21)–(6.24) та врахувавши невід’ємність , , 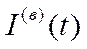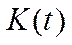(невід’ємність 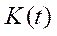випливає з невід’ємності та рівності (6.23)) для економіки, що в кожний момент часу 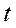характеризується показниками 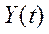, , 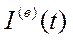, 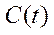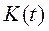(трудові ресурси задаються екзогенно і є сталими), отримаємо в абсолютних показниках один із перших варіантів моделі економічного росту Рамсея

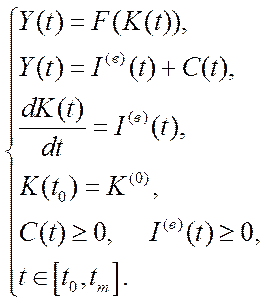(6.25)

Модель (6.25) стала основою для розробки оптимальних програм розвитку економіки з використанням таких інструментів економічної політики, як інвестиції та споживання.

Рамсей запропонував із усіх можливих програм розвитку економіки (із усіх можливих обсягів 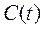та 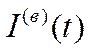, що належать допустимій множині (6.25)), вибрати таку, яка максимізує критерій якості програми росту економіки. Як критерій був вибраний функціонал корисності

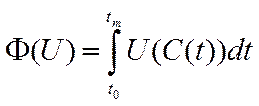, (6.26)

де 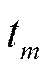– термінальний момент часу, (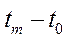) – так званий горизонт планування, 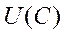– задана функція корисності, що характеризує ступінь задоволення споживачів у поточний момент часу . Функціонал (6.26) є в певному розумінні „сумарною” корисністю невиробничого споживання на проміжку часу 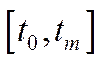. Як функцію корисності в деяких найпростіших випадках можна вибрати лінійну функцію .

Насправді Рамсей розглядав ситуацію, коли 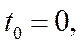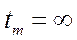. Ми будемо розглядати лише скінченні моменти часу 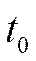, 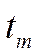(це дозволяє уникнути деяких математичних тонкощів), хоча підкреслимо, що проблема вибору проміжку 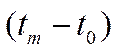заслуговує на самостійне дослідження як з погляду математики, так і з погляду економіки, причому у випадку скінченного 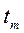задається ще мінімально допустимий рівень капіталоозброєності

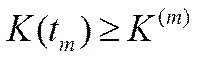. (6.27)

Задача оптимізації програми розвитку економіки полягає в тому, щоб вибрати такі споживання 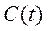та інвестиції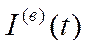, які задовольняють обмеження (6.25), (6.27) і максимізують критерій якості (6.26).

Якщо позначити допустиму множину (6.25), (6.27) через 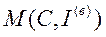, то дана задача може бути формалізована ще так:

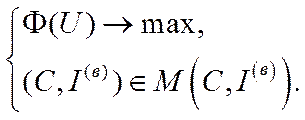(6.28)

Задача (6.28), власне кажучи, описує один із найпростіших варіантів моделі оптимального економічного росту Рамсея.
У математичному плані ця модель належить до класу задач оптимального керування зі змішаними обмеженнями, тобто обмеженнями на функції керування 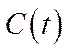, 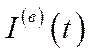(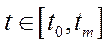) та фазову траєкторію ().

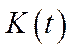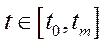Не зупиняючись на математичному дослідженні моделі (6.28), зауважимо лише, що ця модель (або задача Рамсея) з’явилася значно раніше, ніж з’явилися методи розв’язування задач оптимального керування, зокрема так званий принцип максимуму Понтрягіна [34, 38], який відкритий лише в 1956 році.

Зауважимо також, що на базі моделей Рамсея сформувалася так звана неокласична теорія економічного росту. Незважаючи на те, що сучасні моделі росту значно складніші й адекватніші до реальності, запропонований Рамсеєм підхід залишився незмінним: економічна система розглядається як об’єкт управління, а економічна політика оцінюється в порівнянні з оптимальною політикою, закладеною в моделях росту, залежно від різних критеріїв якості.

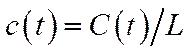Щоб отримати еквівалентну до (6.25) модель у відносних показниках, конкретизуємо їх: – фондо-озброєність, – невиробниче споживання на одного працівника, 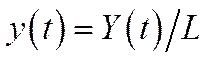– продуктивність праці, 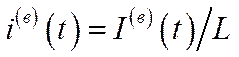– питомі валові інвестиції. Тоді з урахуванням того, що всі показники є функціями часу, крім 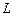, а також лінійної однорідності ВФ, маємо:

,

,

,

.

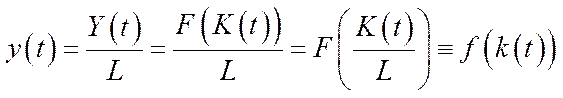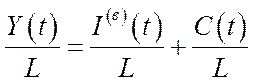Отже, у відносних показниках модель економічного росту (6.25) має вигляд:

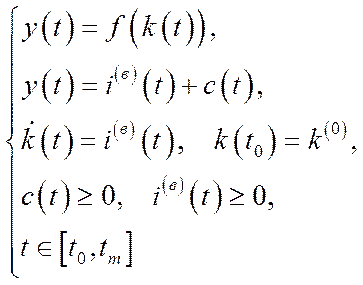(6.29)

або з огляду на те, що 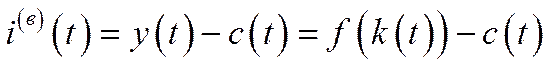, перших два співвідношення можна неявно включити у третє співвідношення і від (6.29) перейти до

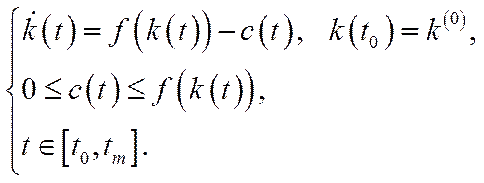(6.30)

Ввівши на основі функції 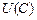функцію корисності 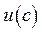, поставимо оптимізаційну задачу: вибрати таке споживання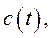 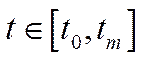, яке задовольняє обмеження (6.27), (6.30) і максимізує функціонал корисності.

Математична формалізація цієї задачі буде моделлю оптимального економічного росту у відносних показниках:

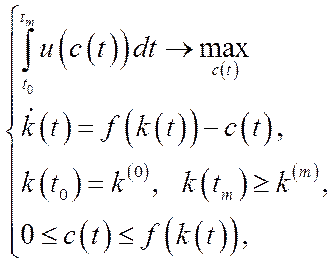(6.31)

де 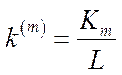, , 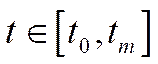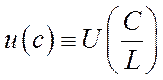. В економіко-математичних дослідженнях, як правило, використовуються моделі у відносних показниках, тобто моделі (6.30), (6.31).

Варіант 2. Зупинимося коротко також на ще одному варіанті моделі, запропонованої Ф. Рамсеєм [48], яка, як і попередня модель, відображає процеси споживання, накопичення та розподілу капітальних вкладень в односекторній економіці й математично формалізує концептуальну модель, описану в пункті (6.1). Конкретизуємо зв’язки (6.1)–(6.3) для економіки, яка в кожний момент часу 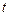також характеризується чотирма величинами 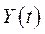, , 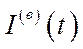, 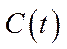(трудові ресурси є сталими і задаються екзогенно).

Нехай 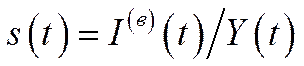– частка кінцевої продукції (норма накопичення капіталу), що витрачається в момент 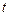на накопичення капіталу 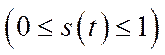, 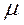– заданий темп амортизації виробничих фондів (капіталу) (тобто 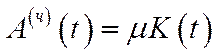), 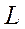– як і раніше, постійна кількість трудових ресурсів, 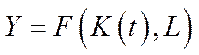– задана функція випуску ВВП чи кінцевої продукції, 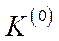– початковий капітал у момент .

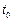Система співвідношень

(6.32)

є ще одним варіантом моделі економічного росту Рамсея. У моделі (6.32) неявно передбачається, що протягом усього розглядуваного проміжку часу основні фонди однорідні та технологічних змін не відбувається.

Зрозуміло, що на основі моделі (6.32) було також запропоновано модель оптимального економічного росту. Якщо як критерій функціонування економіки на проміжку 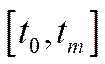взяти „сумарне” питоме споживання (споживання на одиницю робочої сили або одного працівника) з дисконтуванням
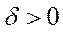(– задана константа),

(6.33)

а значення капіталу в термінальний момент часу 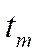обмежити нерівністю (6.27), яка означає, що за межами періоду 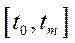обов’язково повинен бути накопичений певний економічний потенціал (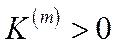– задане), то оптимізаційна задача для керуючого органу (керуючої підсистеми) визначається так: потрібно вибрати таке керування 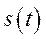, , 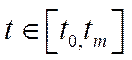яке на допустимій множині співвідношень (6.27), (6.32) максимізує функціонал споживання (6.33).

Ця задача конкретизує в математичній формі ще один варіант моделі оптимального економічного росту Рамсея.

Моделлю-еквівалентом до моделі (6.32), тобто відповідною моделлю економічного росту у відносних показниках буде модель

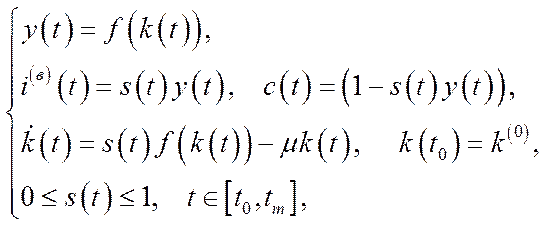(6.34)

де

, ,

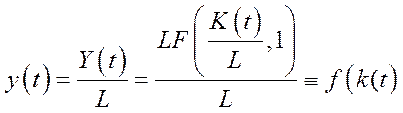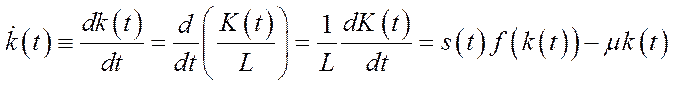а інші уточнення зроблені вище.

Користуючись (6.27) і (6.34) на основі оптимізаційної моделі (6.27), (6.32), (6.33), легко виписати у відносних показниках модель-еквівалент оптимального економічного росту

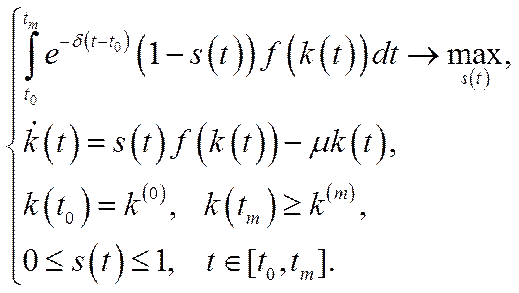(6.35)

Зазначимо, що в описаних вище моделях розглядається скінченний проміжок часу 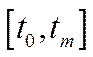, причому оптимізаційні моделі, наприклад (6.31) і (6.35), є в математичному плані задачами оптимального керування [14].

Варіант 3. Моделі (6.32) та (6.34), а також їх оптимізаційні розширення легко модифікуються, якщо трудові ресурси вважати не сталою, а змінною величиною, зокрема вважати, що

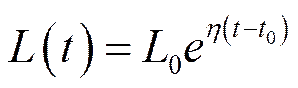,(6.36)

де – кількість працівників у початковий момент часу, 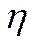– річний темп приросту кількості зайнятих. Очевидно, що (6.36) є розв’язком задачі Коші

,.

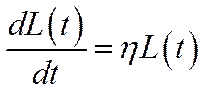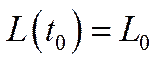У цьому випадку з урахуванням (6.36) зміниться лише диференціальне рівняння в моделях із відносними показниками, оскільки

=

=

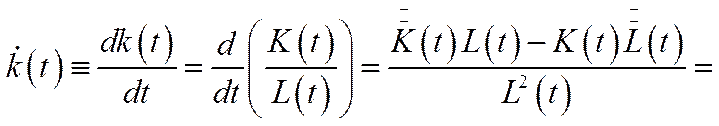
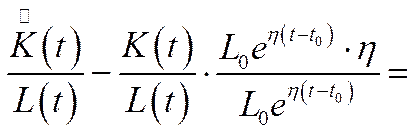
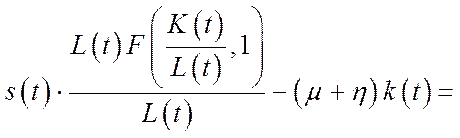
(6.37)

Це означає, що для отримання моделей у відносних показниках у даному разі потрібно лише в моделях (6.34) і (6.35) замість наявного диференціального рівняння записати диференціальне рівняння (6.37).

Наголосимо, що тут йдеться про економіку, яка характеризується в кожний момент часу п’ятьма величинами , , , ,.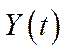

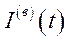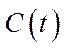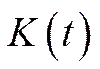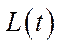Читайте також:

1. Автокореляція залишків – це залежність між послідовними значеннями стохастичної складової моделі.
2. Агітація за і проти та деякі особливості її техніки.
3. АЛОМОРФИ І ВАРІАНТИ МОРФЕМ
4. Альтернативні варіанти геополітичної орієнтації України
5. Альтернативні варіанти довгострокового фінансування діяльності підприємства
6. Аналіз економічноїї політики за допомогою моделі Мандела-Флемінга. Випадки вільного та фіксованого валютного курсів.
7. Аналітичний підбір математичної моделі.
8. Бізнес-моделювання в системі управління розвитком підприємства. Поняття та етапи формування бізнес-моделі
9. Варіанти акультураційних стратегій
10. Варіанти вибору ділової їжі (буфет або a la carte).
11. Варіанти вибору ринкових сегментів
12. ВАРІАНТИ ВИКОРИСТАННЯ ПРОГНОЗІВ В ОРГАНІЗАЦІЇ

Переглядів: 913