• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Продуктивність і нерозкладність моделі Неймана

Поняття продуктивності моделі Неймана вводиться за аналогією з моделлю Леонтьєва, оскільки існує повна аналогія між власними числами (невід’ємними) технологічної матриці А в моделі Леонтьєва та числами 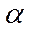(темпами росту), що фігурують у невироджених положеннях рівноваги моделі Неймана.

Виявляється, що продуктивність моделі Неймана повністю визначається значенням її числа Фробеніуса, а розкладність моделі залежить від числа її темпів росту.

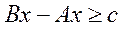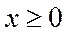
Означення 5.17. Якщо система нерівностей , 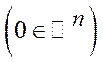має розв’язок при будь-якому 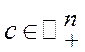, то модель Неймана 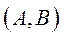називається продуктивною.

Теорема 5.17 (критерій продуктивності моделі Неймана). Для того, щоб модель Неймана була продуктивною необхідно й достатньо, щоб її число Фробеніуса було меншим від одиниці: .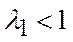

Щоб сформулювати твердження про залежність властивостей моделі Неймана від числа її темпів росту, введемо деякі поняття.

Нехай і 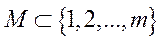деякі непорожні підмножини номерів галузей і продуктів відповідно.

Означення 5.18. Пару множин 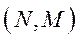будемо називати ізольованою, якщо з того, що 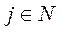, 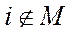випливають рівності .

Якщо в моделі Неймана 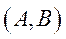існує ізольована пара 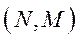, то це означає, що галузі з множини 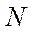не споживають і не виробляють продукцію з номерами 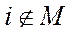, тобто ці галузі утворюють підекономіку з простором товарів меншої розмірності.

Означення 5.19. Модель Неймана 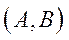, для якої існує ізольована пара 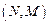, називається розкладною. У протилежному випадку модель Неймана 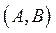буде нерозкладною.

Для розкладної моделі Неймана відповідною перестановкою стовпчиків і рядків матриць А та В їх можна звести до вигляду

, ,

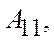
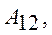
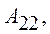
де 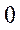– матриці-блоки.

Теорема 5.18 (про розкладність моделі Неймана). Модель Неймана 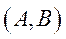розкладна, якщо її числа Неймана і Фробеніуса не збігаються .

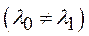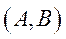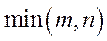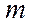Теорема 5.19 (про кількість темпів росту моделі Неймана). Модель Неймана може мати лише скінченне число темпів росту, яке не перевищує величини , де та 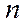– відповідно кількість рядків і стовпців матриць А, В.

Теорема 5.20 (про єдиність темпу росту нерозкладної моделі Неймана). Якщо модель Неймана 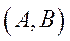нерозкладна, то вона має єдиний темп росту.

З теореми 5.20 випливає, що єдиному темпу росту нерозкладної моделі Неймана не обов’язково відповідає єдине положення рівноваги, оскільки воно залежить від кількості векторів 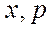, які в сукупності з темпом росту формують положення рівноваги.

Нагадаємо, що модель Неймана узагальнена Гейлом [4]. Але таке узагальнення тут розглядати не будемо, як і інші моделі нейманівського типу.

25. Концептуальна модель односекторної економіки. Неокласичні макровиробничі функції.

Під односекторною однопродуктовою економікою будемо розуміти економіку (як цілісну систему), яка виробляє єдиний універсальний продукт, який може як споживатись, так й інвестуватись. Концептуальна схема (модель) такої економіки наведена нище:

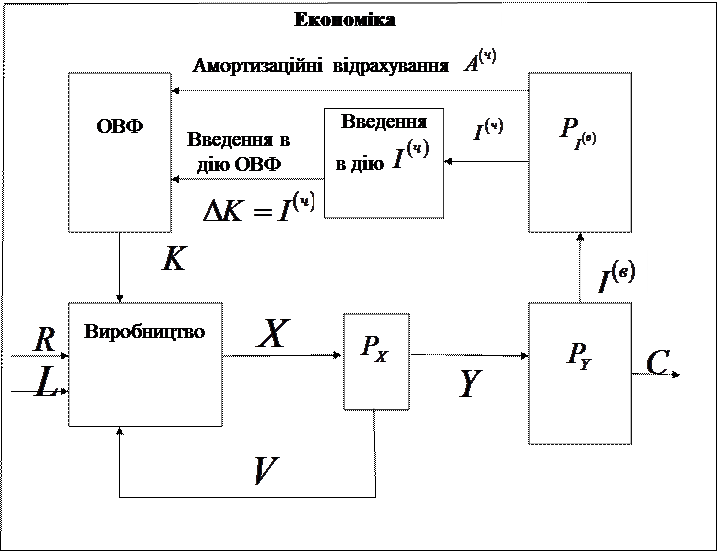
Прийняті такі позначення: 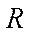– природні ресурси, 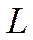– трудові ресурси (кількість зайнятих працівників), 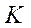– засоби праці або ОВФ, 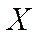– валовий випуск, – виробниче споживання (проміжна продукція), 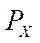– блок розподілу валового випуску, 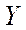– ВВП (кінцева продукція),
– блок розподілу ВВП, 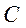– невиробниче споживання (фонд невиробничого споживання), 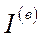– валові капітальні вкладення (валові інвестиції), 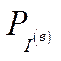– блок розподілу валових капітальних вкладень, 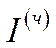– чисті капітальні вкладення (чисті інвестиції), 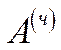– амортизаційні відрахування, 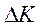– приріст ОВФ ().

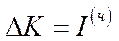З даної концептуальної моделі випливають такі базові співвідношення:

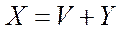, (6.1)

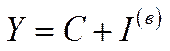, (6.2)

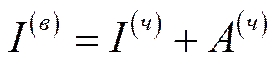. (6.3)

Зміст рівностей (6.1)–(6.3) очевидний. Не зупиняючись на деталізації (6.1)–(6.3), зазначимо лише, що вони є основою для побудови математичних моделей економічного росту, до яких ми повернемося пізніше.

МВФ – це функції, які є моделями або під моделями процесів та систем на макрорівні. Отже, надалі будемо мати справу з МВФ

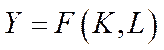. (6.4)

Функція (6.4) називається неокласичною МВФ, якщо вона двічі неперервно диференційовна та задовольняє наступні властивості:

1) (6.5)

– за відсутності хоча б одного ресурсу виробництво неможливе;

2) 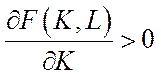, 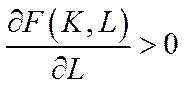(6.6)

– збільшення витрат виробничих фондів і робочої сили призводить до зростання випуску продукції;

3) , 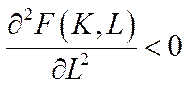(6.7)

– в умовах екстенсивного розвитку економіки збільшення витрат лише одного виробничого ресурсу (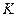або 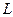) призводить до падіння ефективності його використання;

4) 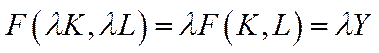(6.8)

– обсяг випуску характеризується постійною віддачею від розширення масштабів виробництва ;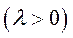

5) , 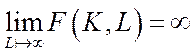(6.9)

– при необмеженому зростанні одного з ресурсів випуск необмежено зростає;

6) 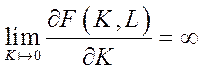, , 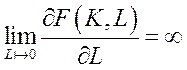(6.10)

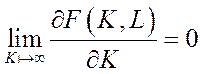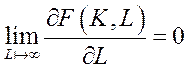, (6.11)

– граничні ефективності фондів та праці необмежено зростають при наближенні відповідних ресурсів до нуля та спадають до нуля при необмеженому зростанні ресурсів.

Стосовно умов (6.7) варто сказати, що дуже часто вони підсилюються аксіомою угнутості чи строгої угнутості МВФ у цілому.

Інколи до макровиробничої функції вводиться змінна часу 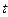, щоб урахувати ряд зовнішніх факторів, зокрема вплив науково-технічного прогресу. Але тут МВФ, що явно залежить від 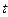, розглядати не будемо.

Зручність функції (6.4), що задовольняє властивості
(6.5)–(6.11), полягає перш за все в тому, що ми можемо замінити її однофакторним еквівалентом, тобто функцією

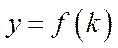, (6.12)

де 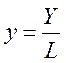– середня продуктивність праці, 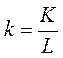– капіталоозброєність (або фондоозброєність), .

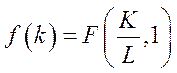На основі (6.5)–(6.11) легко встановити, що для функції (6.12) виконуються такі умови:

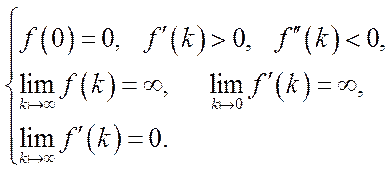(6.13)

Двічі неперервно диференційовна функція (6.12), що задовольняє обмеження (6.13), називається однофакторною неокласичною виробничою функцією.

26.Модель оптимального економічного росту рамсеївського типу.

Читайте також:

1. Автокореляція залишків – це залежність між послідовними значеннями стохастичної складової моделі.
2. Аналіз економічноїї політики за допомогою моделі Мандела-Флемінга. Випадки вільного та фіксованого валютного курсів.
3. Аналітичний підбір математичної моделі.
4. Бізнес-моделювання в системі управління розвитком підприємства. Поняття та етапи формування бізнес-моделі
5. Біологічні особливості, продуктивність та породи коней
6. Будівельна продукція. Кадри, нормування і продуктивність праці
7. Вибір підходу до процесу соціальної роботи зале­жить від теоретичної моделі, якої дотримуються соці­альні працівники, обраної стратегії втручання і методу соціальної роботи.
8. Види світогляду: міфологічний, релігійний та філософський (натуралістична, об’єктивно-ідеалістична, субєктивно-ідеалістичні і матеріалістичні моделі).
9. Використання моделі Хікса – Хансена для оцінки відносної ефективності бюджетно-податкової і кредитно-грошової політики
10. Виникнення суб'єктивних прав і юридичних обов'язків — перехід від загальних приписів правових норм до конкретної моделі поведінки конкретних господарюючих суб'єктів.
11. Відповідність рівнів стека TCP/IP семирівневої моделі ISO/OSI
12. Вовнова продуктивність

Переглядів: 813