
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Динамічна рівновага в моделі Неймана
Таблиця 5.5
| Галузі- виробники | Галузі-споживачі | Кінцева продукція | Валова продукція | |||||||
| Міжгалузеві потоки засобів виробництва | Міжгалузеві потоки капітальних вкладень | |||||||||
| ... | 
| ... | 
| |||||||

| 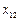
| ... | 
| 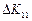
| 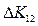
| ... | 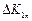
| 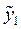
| 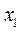
| |

| 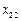
| ... | 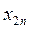
| 
| 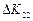
| ... | 
| 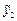
| 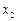
| |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |

| 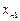
| 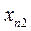
| ... | 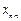
| 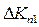
| 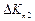
| ... | 
| 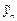
| 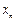
|
У таблиці 5.5 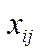 – це міжгалузеві потоки засобів виробництва в поточному періоді;
– це міжгалузеві потоки засобів виробництва в поточному періоді; 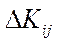 – кількість продукції
– кількість продукції
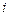 -тої галузі, що направляється в поточному періоді в
-тої галузі, що направляється в поточному періоді в 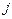 -ту галузь як капітальні вкладення в її основні фонди (фактично це виявляється для галузей-споживачів у прирості виробничого обладнання, виробничих площ, транспортних засобів тощо);
-ту галузь як капітальні вкладення в її основні фонди (фактично це виявляється для галузей-споживачів у прирості виробничого обладнання, виробничих площ, транспортних засобів тощо);
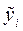 – чиста кінцева продукція
– чиста кінцева продукція 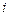 -тої галузі (вона включає в себе продукцію, що використовується на кінцеве споживання (індивідуальне та суспільне), чистий експорт, накопичення невиробничої сфери, приріст оборотних фондів, капітальний ремонт тощо). Як випливає з таблиці 5.5, у схемі ДМБ кінцева продукція кожної
-тої галузі (вона включає в себе продукцію, що використовується на кінцеве споживання (індивідуальне та суспільне), чистий експорт, накопичення невиробничої сфери, приріст оборотних фондів, капітальний ремонт тощо). Як випливає з таблиці 5.5, у схемі ДМБ кінцева продукція кожної 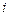 -тої галузі дорівнює сумі потоків капіталовкладень та чистої кінцевої продукції, тобто
-тої галузі дорівнює сумі потоків капіталовкладень та чистої кінцевої продукції, тобто
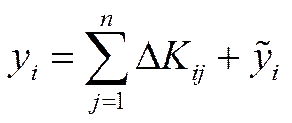 .
.
З урахуванням останньої рівності розподіл продукції всіх галузей формалізується так:
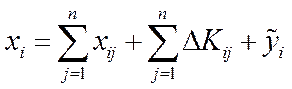 ,
, . (5.36)
. (5.36)
Трансформуємо співвідношення (5.36), ввівши змінну часу. При цьому будемо вважати, що приріст 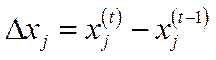 продукції поточного періоду
продукції поточного періоду 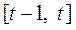 зумовлений капітальними вкладеннями, зробленими в цьому ж періоді. Припускаючи також, що капіталовкладення прямо пропорційні приросту продукції, отримаємо
зумовлений капітальними вкладеннями, зробленими в цьому ж періоді. Припускаючи також, що капіталовкладення прямо пропорційні приросту продукції, отримаємо
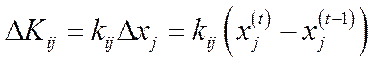 ,
, 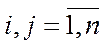 , (5.37)
, (5.37)
де коефіцієнти пропорційності 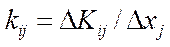 ,
,  , називаються коефіцієнтами вкладень, або коефіцієнтами приросту фондомісткості. Економічний зміст цих коефіцієнтів очевидний. Вони показують, яка кількість продукції
, називаються коефіцієнтами вкладень, або коефіцієнтами приросту фондомісткості. Економічний зміст цих коефіцієнтів очевидний. Вони показують, яка кількість продукції 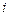 -тої галузі повинна бути вкладена в
-тої галузі повинна бути вкладена в 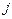 -ту галузь для збільшення виробничої потужності
-ту галузь для збільшення виробничої потужності 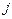 -тої галузі на одиницю продукції. Зауважимо, що коефіцієнти
-тої галузі на одиницю продукції. Зауважимо, що коефіцієнти 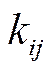 ,
,  можуть також залежати від часу, хоча в рамках пропонованого варіанта динамічної моделі міжгалузевого балансу ми будемо вважати їх сталими величинами.
можуть також залежати від часу, хоча в рамках пропонованого варіанта динамічної моделі міжгалузевого балансу ми будемо вважати їх сталими величинами.
Якщо зважати на те, що всі обсяги валової й кінцевої продукції належать до конкретного моменту часу 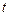 , а приріст валової продукції визначається в порівнянні з
, а приріст валової продукції визначається в порівнянні з 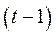 -м моментом часу (наприклад поточний і попередній роки), то, використавши (5.36) і (5.37), отримаємо співвідношення
-м моментом часу (наприклад поточний і попередній роки), то, використавши (5.36) і (5.37), отримаємо співвідношення
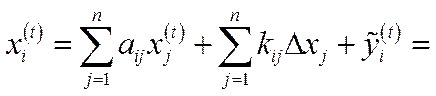
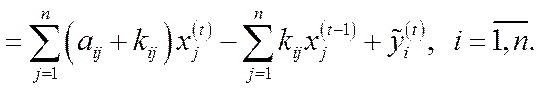 (5.38)
(5.38)
Якщо відомі 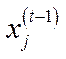 ,
, 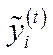 ,
, 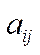 ,
, 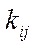 ,
, 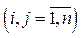 , то динамічна модель (5.38) буде системою
, то динамічна модель (5.38) буде системою  лінійних рівнянь із
лінійних рівнянь із  невідомими
невідомими  ,
, 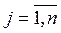 . Інакше кажучи, система (5.38) дозволяє визначити випуск валової продукції в наступний період (момент) часу залежно від валового випуску в попередній період.
. Інакше кажучи, система (5.38) дозволяє визначити випуск валової продукції в наступний період (момент) часу залежно від валового випуску в попередній період.
У математичному плані модель (5.38) дискретна. Очевидно, базуючись на (5.38), можна запропонувати також неперервний варіант динамічної моделі міжгалузевого балансу
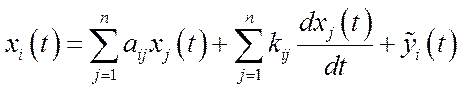 ,
,  . (5.39)
. (5.39)
Система (5.39) є системою  лінійних диференціальних рівнянь першого порядку зі сталими коефіцієнтами. Для її розв’язання, крім
лінійних диференціальних рівнянь першого порядку зі сталими коефіцієнтами. Для її розв’язання, крім 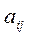 ,
, 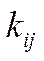 та
та 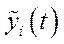
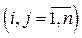 , потрібно також задати значення валових випусків у початковий момент часу
, потрібно також задати значення валових випусків у початковий момент часу  . Розв’язавши отриману задачу Коші, знайдемо шуканий валовий випуск у будь-який момент часу
. Розв’язавши отриману задачу Коші, знайдемо шуканий валовий випуск у будь-який момент часу 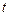 , хоча найбільш реальні дані можна отримати лише для невеликих проміжків часу. Зробимо кілька зауважень.
, хоча найбільш реальні дані можна отримати лише для невеликих проміжків часу. Зробимо кілька зауважень.
· Cтосовно дискретної моделі (5.38) зазначимо, що для порівняно коротких періодів часу 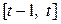 припущення (5.37) може виявитись нереальним, оскільки існують відставання в часі (так звані лаги) між капіталовкладеннями й приростом випуску продукції. У зв’язку з цим актуальні також моделі, які враховують лаг капітальних вкладень.
припущення (5.37) може виявитись нереальним, оскільки існують відставання в часі (так звані лаги) між капіталовкладеннями й приростом випуску продукції. У зв’язку з цим актуальні також моделі, які враховують лаг капітальних вкладень.
· Ще одне зауваження стосується припущення про те, що в період 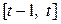 виробничі потужності використовуються повністю, тому сумарний приріст продукції
виробничі потужності використовуються повністю, тому сумарний приріст продукції 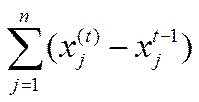 досягається за рахунок капіталовкладень
досягається за рахунок капіталовкладень 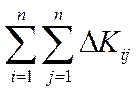 . В умовах перехідної (трансформаційної) економіки, яка характеризується падінням виробництва, а отже, неповним використанням виробничих потужностей, дане припущення частково порушується. У зв’язку з цим використання моделі в умовах нестабільної та циклічної економіки проблематичне. Однак цінність результатів, отриманих на основі розрахунків із моделлю, не зменшується, особливо під час визначення обсягів виробництва в галузях при загальному обсязі чистої кінцевої продукції, величина якої близька до фонду кінцевого споживання (з огляду на інертність цього показника нескладно отримати його оцінку).
. В умовах перехідної (трансформаційної) економіки, яка характеризується падінням виробництва, а отже, неповним використанням виробничих потужностей, дане припущення частково порушується. У зв’язку з цим використання моделі в умовах нестабільної та циклічної економіки проблематичне. Однак цінність результатів, отриманих на основі розрахунків із моделлю, не зменшується, особливо під час визначення обсягів виробництва в галузях при загальному обсязі чистої кінцевої продукції, величина якої близька до фонду кінцевого споживання (з огляду на інертність цього показника нескладно отримати його оцінку).
· Особливу роль у динамічній моделі відіграють коефіцієнти приросту фондомісткості 
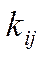
 . Кожний стовпчик матриці цих коефіцієнтів характеризує для відповідної
. Кожний стовпчик матриці цих коефіцієнтів характеризує для відповідної 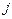 -тої галузі величину й структуру фондів, необхідних для збільшення виробничих потужностей (випуску продукції) на одну одиницю. Коефіцієнти приросту фондомісткості певним чином пов’язані з прямими коефіцієнтами фондомісткості. Це використовується при побудові динамічних моделей, оскільки дані про фондомісткості продукції отримати завжди легше, ніж розрахувати коефіцієнти вкладень.
-тої галузі величину й структуру фондів, необхідних для збільшення виробничих потужностей (випуску продукції) на одну одиницю. Коефіцієнти приросту фондомісткості певним чином пов’язані з прямими коефіцієнтами фондомісткості. Це використовується при побудові динамічних моделей, оскільки дані про фондомісткості продукції отримати завжди легше, ніж розрахувати коефіцієнти вкладень.
23. Аналіз оптимальних траєкторій динамічної моделі Леонтьєва засобами магістральної теорії.
Динамічні моделі менш ідеалізовані та більш адекватні щодо реальної дійсності. У попередньому пункті розглянуто лише один із варіантів динамічної моделі міжгалузевого балансу, на основі якої можна побудувати допустиму траєкторію розвитку багатогалузевої економіки на певному відрізку часу. Можна також розглянути багато інших варіантів динамічного міжгалузевого балансу, зокрема в основі багатьох більш складних і змістовних моделей, що використовуються в практиці планування й прогнозування, лежить так звана
 -модель [1, 25, 30, 39]. Однак в економіко-математичній теорії розроблена загальна динамічна модель багатогалузевої економіки Неймана [1], яка містить у собі як окремий випадок більш прості варіанти моделей динамічного міжгалузевого балансу і буде описана пізніше. Реальна модель такого типу,
-модель [1, 25, 30, 39]. Однак в економіко-математичній теорії розроблена загальна динамічна модель багатогалузевої економіки Неймана [1], яка містить у собі як окремий випадок більш прості варіанти моделей динамічного міжгалузевого балансу і буде описана пізніше. Реальна модель такого типу,
по-перше, є задачею великої розмірності, а по-друге, є оптимізаційною задачею, оскільки потрібно вибрати не просто траєкторію, а оптимальну траєкторію розвитку багатогалузевої економіки. Знайти розв’язки таких задач складно або й неможливо. У зв’язку з цим розвинена теорія якісних методів дослідження оптимальних траєкторій моделей нейманівського типу, зокрема магістральна теорія, елементи якої проілюструємо нижче на прикладі одного з найпростіших варіантів оптимізаційної динамічної моделі Леонтьєва.
Як і раніше, розглянемо економічну систему, що складається з  „чистих” галузей, причому
„чистих” галузей, причому  – матриця міжгалузевого балансу,
– матриця міжгалузевого балансу,  – вектор валової продукції,
– вектор валової продукції, 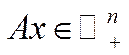 – вектор проміжної продукції (вектор виробничих витрат). Нехай виробничий процес досліджується на проміжку часу
– вектор проміжної продукції (вектор виробничих витрат). Нехай виробничий процес досліджується на проміжку часу 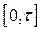 , який поділений на
, який поділений на 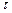 періодів:
періодів: 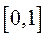 ,
, 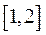 , ...,
, ..., 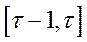 . Кожному моменту часу
. Кожному моменту часу 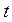
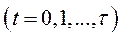 відповідає свій вектор валової продукції
відповідає свій вектор валової продукції 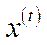 , який при
, який при  використовується як вектор виробничих ресурсів для виробничого циклу в наступний період
використовується як вектор виробничих ресурсів для виробничого циклу в наступний період 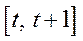 . Очевидно, вибір вектора
. Очевидно, вибір вектора 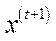 можна здійснити різними способами, тому перед дослідником постає природне запитання про знаходження деякої оптимальної траєкторії
можна здійснити різними способами, тому перед дослідником постає природне запитання про знаходження деякої оптимальної траєкторії  динамічного процесу виробництва, в якій початковий стан
динамічного процесу виробництва, в якій початковий стан 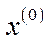 заданий. Якщо, крім того, задати вектор цін
заданий. Якщо, крім того, задати вектор цін 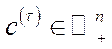 на продукцію в кінці планового періоду (тобто в момент
на продукцію в кінці планового періоду (тобто в момент 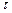 ), то можна поставити таку оптимізаційну задачу: побудувати таку траєкторію
), то можна поставити таку оптимізаційну задачу: побудувати таку траєкторію 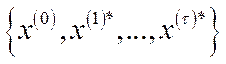 розвитку
розвитку -галузевої економіки, яка б при заданих
-галузевої економіки, яка б при заданих 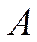 ,
, 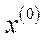 ,
, 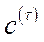 та відповідних технологічних обмеженнях максимізувала вартість продукції
та відповідних технологічних обмеженнях максимізувала вартість продукції  (або вартість термінального стану економіки). Математична модель цієї задачі має такий вигляд:
(або вартість термінального стану економіки). Математична модель цієї задачі має такий вигляд:
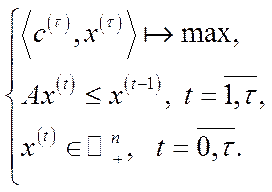 (5.40)
(5.40)
У моделі (5.40) нерівність 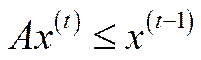 формалізує технологічне обмеження в період часу
формалізує технологічне обмеження в період часу 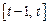 і означає, що виробничі витрати в цей період не можуть перевищувати виробничих (ресурсних) запасів, які сформувались на початок даного періоду. В економіко-математичній літературі модель (5.40) часто називають динамічною моделлю Леонтьєва, опускаючи термін „оптимізаційна”, хоча насправді вона є саме такою. Як уже було сказано вище, ця модель, як частинний варіант моделі Неймана, узагальнює схему задання технології виробничого процесу. В математичному плані модель (5.40) є стандартною задачею лінійного програмування [7, 36], дослідження якої дозволить нам продемонструвати суть магістральної теорії.
і означає, що виробничі витрати в цей період не можуть перевищувати виробничих (ресурсних) запасів, які сформувались на початок даного періоду. В економіко-математичній літературі модель (5.40) часто називають динамічною моделлю Леонтьєва, опускаючи термін „оптимізаційна”, хоча насправді вона є саме такою. Як уже було сказано вище, ця модель, як частинний варіант моделі Неймана, узагальнює схему задання технології виробничого процесу. В математичному плані модель (5.40) є стандартною задачею лінійного програмування [7, 36], дослідження якої дозволить нам продемонструвати суть магістральної теорії.
Перш за все, запишемо ресурсні обмеження в скалярному вигляді:


де 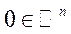 .
.
У зв’язку з цими обмеженнями введемо вектори 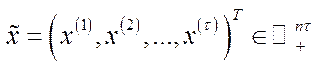 ,
, 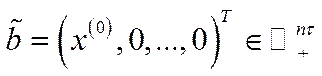 ,
,  та матрицю
та матрицю
 ,
,
елементами якої є квадратні матриці розмірності 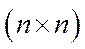 .
.
Тоді задача лінійного програмування (5.40) запишеться так:
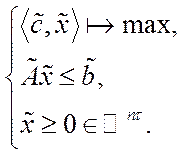 (5.41)
(5.41)
Двоїстою до (5.41) буде задача
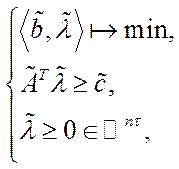 (5.42)
(5.42)
де 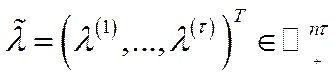 .
.
Очевидно, від (5.42) можна перейти до більш деталізованої задачі
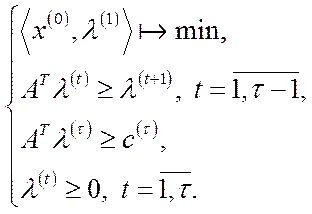 (5.43)
(5.43)
Задача (5.43) є задачею мінімізації вартості початкових ресурсів.
Усі сформульовані вище задачі (тобто задачі (5.40)–(5.43)) є задачами великої розмірності. Практично розв’язати їх вдається не завжди, тому виникає питання про якісний аналіз оптимальних траєкторій, тобто про дослідження поведінки цих траєкторій без їх наявної конкретизації. Такими питаннями займається магістральна теорія.
Щоб сформулювати основний результат цієї теорії стосовно моделі (5.40), введемо спочатку ряд допоміжних понять.
Означення 5.6. Число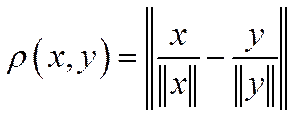 ,
,
де 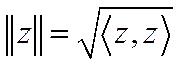 – евклідова норма, називається квазіметрикою, або мірою „кутової” відстані між векторами
– евклідова норма, називається квазіметрикою, або мірою „кутової” відстані між векторами 
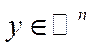
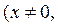
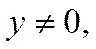
 .
.
Очевидно, число 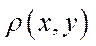 є довжиною вектора
є довжиною вектора  , що є різницею двох нормованих векторів. Зазначимо очевидні властивості квазіметрики
, що є різницею двох нормованих векторів. Зазначимо очевидні властивості квазіметрики  :
:
·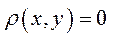 тоді і лише тоді, коли вектори
тоді і лише тоді, коли вектори 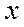 ,
, 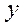 колінеарні;
колінеарні;
·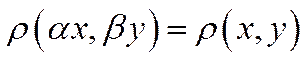 для всіх чисел
для всіх чисел 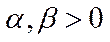 ;
;
·якщо при 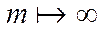
 ,
, 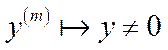 , то
, то 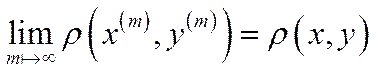 ;
;
·для будь-яких 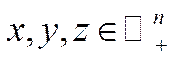
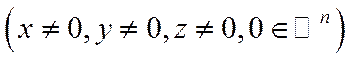
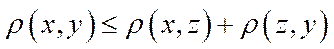 .
.
Означення 5.7. Промінь 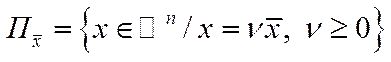
називається магістраллю для задачі (1.40), якщо для будь-якого  існують такі числа
існують такі числа 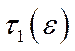 і
і 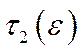 , що для довільної оптимальної траєкторії
, що для довільної оптимальної траєкторії 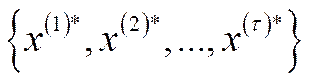 виконується нерівність
виконується нерівність 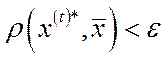 для всіх
для всіх  .
.
Інколи магістраллю називають просто вектор 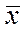 , який породжує промінь
, який породжує промінь 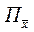 .
.
Довільне твердження про наявність магістралі називається теоремою про магістраль.
Значення теореми про магістраль полягає в тому, що промінь 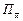 дає апроксимацію оптимальних траєкторій. Інакше кажучи, оптимальна траєкторія „майже весь час” знаходиться у „вузькому” конусі, вісь симетрії якого колінеарна до магістралі
дає апроксимацію оптимальних траєкторій. Інакше кажучи, оптимальна траєкторія „майже весь час” знаходиться у „вузькому” конусі, вісь симетрії якого колінеарна до магістралі 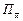 . Звичайно, проміжок
. Звичайно, проміжок 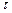 вважається досить великим:
вважається досить великим:  . Числа
. Числа 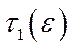 і
і 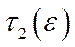 не залежать від планового горизонту
не залежать від планового горизонту 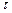 , а сам вектор
, а сам вектор 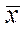 „мало залежить” від зміни цільового функціонала
„мало залежить” від зміни цільового функціонала  . Усе це випливає із строгих математичних обґрунтувань.
. Усе це випливає із строгих математичних обґрунтувань.
Щоб сформулювати теорему про магістраль для задачі (5.40), наведемо визначення примітивної матриці. Як відомо, невід’ємні матриці можна поділити на два класи: розкладні й нерозкладні. Нерозкладні матриці також поділяються на два класи: циклічні та примітивні. Змістовність такого поділу легко обґрунтувати.
Означення 5.8.Нерозкладна матриця 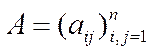 називається циклічною (або імпримітивною), якщо множину
називається циклічною (або імпримітивною), якщо множину 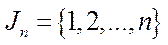 можна подати у вигляді
можна подати у вигляді 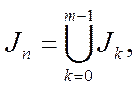
 ,
, 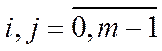 , причому, якщо
, причому, якщо 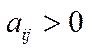 ,
,  ,
, 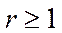 , то
, то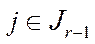 , а при
, а при  індекс
індекс 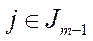 .
.
Одночасною перестановкою рядків та стовпчиків циклічної матриці 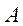 її можна звести до вигляду
її можна звести до вигляду
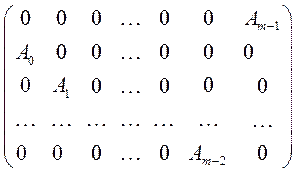 ,
,
де розмірність квадратної матриці 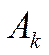
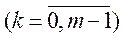 збігається з кількістю елементів у множині
збігається з кількістю елементів у множині  .
.
Означення 5.9.Нерозкладна матриця 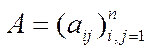 , яка не є циклічною, називається примітивною.
, яка не є циклічною, називається примітивною.
Справедливе наступне твердження, яке ми формулюємо без доведення.
Теорема 5.14 (теорема Морішими про магістраль для динамічної моделі Леонтьєва з термінальним функціоналом).Нехай у задачі (5.40) матриця 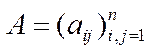 – невід’ємна, нерозкладна та примітивна, а вектори
– невід’ємна, нерозкладна та примітивна, а вектори 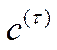 і
і 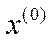 – додатні. Тоді магістраллю для задачі (5.40) буде правий вектор Фробеніуса
– додатні. Тоді магістраллю для задачі (5.40) буде правий вектор Фробеніуса 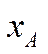 матриці
матриці 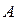 .
.
Доведення цієї теореми можна знайти в [1, 39]. Засобами магістральної теорії досліджено багато задач, аналогічних до (5.40), зокрема задачі з нетермінальним, тобто інтегральним цільовим функціоналом, однак розгляд таких задач і відповідних їм моделей виходить за рамки даного посібника.
24. Модель Неймана. Поняття динамічної рівноваги, продуктивності й нерозкладності для моделі Неймана.
Як було зазначено вище, динамічні моделі міжгалузевого балансу є частинним випадком моделі Неймана [1, 39], в якій допускається сумісне виробництво в кожному технологічному процесі (в кожній галузі) декілька видів продукції. Це усуває основний недолік схеми Леонтьєва – припущення про чисті галузі (кожна галузь виробляє єдиний продукт і єдиним технологічним способом).
Модель Неймана задається парою невід’ємних матриць  , де
, де 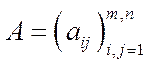 – матриця витрат,
– матриця витрат, 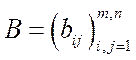 – матриця випуску. Якщо позначити через
– матриця випуску. Якщо позначити через  ,
, 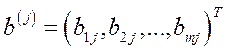 –
– 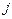 -ті вектори-стовпці матриць А, В, то пара
-ті вектори-стовпці матриць А, В, то пара 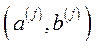 описує виробничий процес, де
описує виробничий процес, де 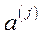 – вектор витрат, а
– вектор витрат, а 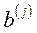 – вектор випуску продукції при функціонуванні даного процесу з одиничною інтенсивністю (
– вектор випуску продукції при функціонуванні даного процесу з одиничною інтенсивністю (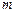 – кількість різних продуктів (кількість рядків),
– кількість різних продуктів (кількість рядків),  – кількість різних технологічних способів (кількість стовпців)).
– кількість різних технологічних способів (кількість стовпців)).
Інтенсивність – це показник [29], за допомогою якого вимірюють "потоки", тобто залежні від часу економічні процеси, наприклад річний випуск продукції, річний обсяг споживання продуктів харчування в країні тощо. Під інтенсивністю 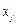 технологічного способу виробництва
технологічного способу виробництва 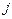 в економіко-
в економіко-
математичній літературі, як правило, розуміють кількість продукції, що випускається моделюючим об’єктом в рік при використанні технології 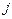 . Одинична інтенсивність – це інтенсивність
. Одинична інтенсивність – це інтенсивність 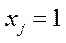 . Скінченний набір виробничих процесів
. Скінченний набір виробничих процесів 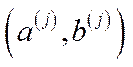 ,
, 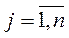 будемо називати набором базисних процесів. Побудуємо новий процес, у якому вектори витрат і випуску є лінійними комбінаціями відповідних базисних процесів:
будемо називати набором базисних процесів. Побудуємо новий процес, у якому вектори витрат і випуску є лінійними комбінаціями відповідних базисних процесів:
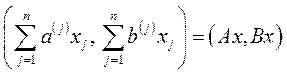 , (5.44)
, (5.44)
де вектор 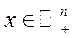 назвемо вектором інтенсивностей (інтенсивностей використання технологічних способів). Виходячи з (5.44) будемо говорити, що
назвемо вектором інтенсивностей (інтенсивностей використання технологічних способів). Виходячи з (5.44) будемо говорити, що 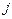 -тий базисний процес
-тий базисний процес 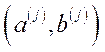 бере участь в процесі
бере участь в процесі 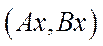 з інтенсивністю
з інтенсивністю 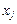 .
.
Нехай  – множина всеможливих процесів або технологічна множина Неймана. Елемент
– множина всеможливих процесів або технологічна множина Неймана. Елемент 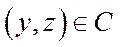 є штучним процесом, а базисні процеси можна вважати такими, що відповідають певним галузям чи підприємствам.
є штучним процесом, а базисні процеси можна вважати такими, що відповідають певним галузям чи підприємствам.
Перейдемо до описання моделі Неймана, в основі якої лежать наступні припущення 1) – 4).
1) Модель Неймана лінійна. Розглядається 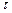 періодів (років, місяців тощо)
періодів (років, місяців тощо) 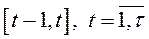 , причому в кожному з періодів
, причому в кожному з періодів 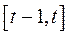 виробництво продукції здійснюється за допомогою одного із процесів множини
виробництво продукції здійснюється за допомогою одного із процесів множини 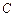 , де
, де 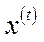 – вектор інтенсивностей.
– вектор інтенсивностей.
2) Модель Неймана замкнута, тобто для виробництва в період  може бути витрачена лише продукція, вироблена в попередньому періоді
може бути витрачена лише продукція, вироблена в попередньому періоді  :
:
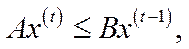
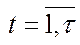 , (5.45)
, (5.45)
де 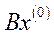 – вектор початкових запасів на початку періоду
– вектор початкових запасів на початку періоду 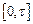 .
.
Послідовність векторів інтенсивностей  , які задовольняють систему нерівностей (5.45), називатимемо планом або траєкторією інтенсивностей.
, які задовольняють систему нерівностей (5.45), називатимемо планом або траєкторією інтенсивностей.
Нехай  – вектор цін на продукцію в період
– вектор цін на продукцію в період 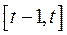 . Прибуток процесу
. Прибуток процесу 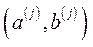 з одиничною інтенсивністю
з одиничною інтенсивністю 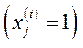 за період
за період 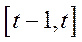 визначається величиною
визначається величиною 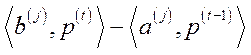 (можна вважати, що на початку періоду
(можна вважати, що на початку періоду 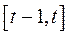 здійснюється покупка сировини за цінами
здійснюється покупка сировини за цінами 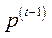 , а потім вироблена продукція вже продається за новими цінами
, а потім вироблена продукція вже продається за новими цінами 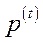 ).
).
3) Жодний з базисних процесів  ,
, 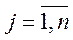 не дає додатного прибутку:
не дає додатного прибутку:
 ,
, 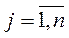 ,
, 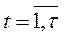
або
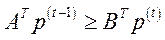 ,
, 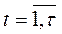 . (5.46)
. (5.46)
Припущення (5.46) називають правилом нульового прибутку, або правилом безприбутковості виробництва. Незважаючи на деяку парадоксальність припущення 3), його все-таки можна трактувати як специфічну властивість замкнутої моделі: із зростанням загальної кількості продуктів (товарів) грошова маса не збільшується.
Послідовність векторів-цін 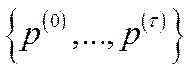 , які задовольняють нерівність (5.46), будемо називати траєкторією цін.
, які задовольняють нерівність (5.46), будемо називати траєкторією цін.
4) Загальна грошова маса не змінюється і постійно знаходиться в обігу:

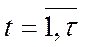 , (5.47)
, (5.47)
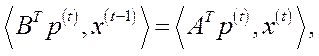
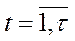 . (5.48)
. (5.48)
Незмінність грошової маси, тобто баланс між вартістю витрат 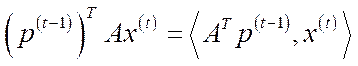 та вартістю випуску продукції
та вартістю випуску продукції 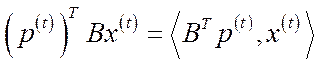 в кожному з періодів
в кожному з періодів 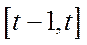 відображається співвідношеннями (5.47). Той факт, що грошова сума весь час знаходиться в обігу, формалізується рівностями (5.48), які означають, що на початку кожного періоду
відображається співвідношеннями (5.47). Той факт, що грошова сума весь час знаходиться в обігу, формалізується рівностями (5.48), які означають, що на початку кожного періоду 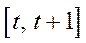 вся сума грошей
вся сума грошей 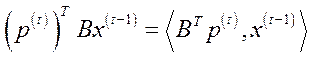 , отримана від продажу продукції попереднього виробничого циклу
, отримана від продажу продукції попереднього виробничого циклу 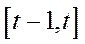 , дорівнює грошовій сумі
, дорівнює грошовій сумі 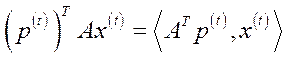 витрат сировини наступного виробничого циклу
витрат сировини наступного виробничого циклу 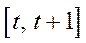 .
.
Динамічна модель Неймана формалізується співвідношеннями (5.45)–(5.48).
При вивченні множин допустимих траєкторій і цін важливу роль відіграють так звані стаціонарні траєкторії – найпростіші з можливих динамічних траєкторій.
Означення 5.10.Траєкторія інтенсивностей 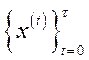 називається стаціонарною, якщо існує таке число
називається стаціонарною, якщо існує таке число 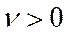 , що
, що  , тобто
, тобто 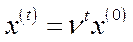 .
.
Означення 5.11. Траєкторія цін 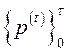 називається стаціонарною, якщо існує таке число
називається стаціонарною, якщо існує таке число 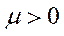 , що
, що 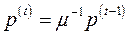 , тобто
, тобто 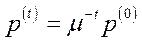 .
.
Підставивши вирази 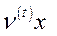 та
та 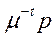 відповідно у (5.45) та (5.46), приходимо до таких тверджень:
відповідно у (5.45) та (5.46), приходимо до таких тверджень:
· послідовність інтенсивностей  буде стаціонарною тоді і лише тоді, коли для числа
буде стаціонарною тоді і лише тоді, коли для числа 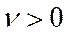 і початкового вектора
і початкового вектора 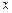 виконується нерівність:
виконується нерівність:
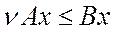 ; (5.49)
; (5.49)
· послідовність цін  буде стаціонарною тоді і лише тоді, коли для числа
буде стаціонарною тоді і лише тоді, коли для числа 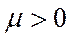 і початкового вектора
і початкового вектора 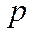 виконується нерівність:
виконується нерівність:
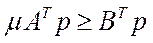 . (5.50)
. (5.50)
Для стаціонарних же траєкторій 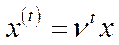 ,
,  співвідношення (5.47), (5.48) конкретизується у вигляді (5.51), (5.52):
співвідношення (5.47), (5.48) конкретизується у вигляді (5.51), (5.52):
 , (5.51)
, (5.51)
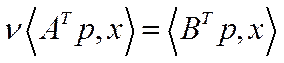 . (5.52)
. (5.52)
Означення 5.12. Модель Неймана знаходиться у стані динамічної рівноваги 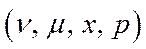 , де числа
, де числа 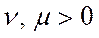 , а
, а
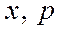 – невід’ємні ненульові вектори, якщо виконуються умови (5.49)–(5.52):
– невід’ємні ненульові вектори, якщо виконуються умови (5.49)–(5.52):
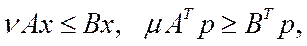
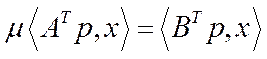 ,
,
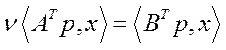 .
.
Величина 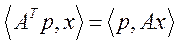 є вартістю витрат в стані рівноваги моделі Неймана. Будемо вважати, що
є вартістю витрат в стані рівноваги моделі Неймана. Будемо вважати, що 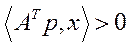 . Тоді з (5.50), (5.51) випливає, що
. Тоді з (5.50), (5.51) випливає, що  .
.
Означення 5.13. Трійка 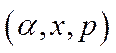 , де число
, де число 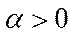 , вектори
, вектори 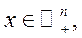
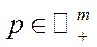 , називається невиродженим положенням рівноваги в моделі Неймана, якщо
, називається невиродженим положенням рівноваги в моделі Неймана, якщо
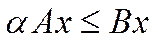 , (5.53)
, (5.53)
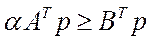 , (5.54)
, (5.54)
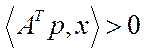 . (5.55)
. (5.55)
Означення 5.14. Нехай вектор  є компонентою невиродженого положення рівноваги. Тоді промінь (множина векторів)
є компонентою невиродженого положення рівноваги. Тоді промінь (множина векторів) 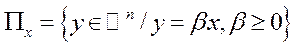 називається променем Неймана (магістраллю).
називається променем Неймана (магістраллю).
Дж. фон Нейман довів, що при деяких обмеженнях на матриці 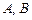 система (5.53)–(5.55), має розв’язок, однак накладені на
система (5.53)–(5.55), має розв’язок, однак накладені на 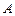 та
та 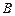 умови не мали чіткої економічної інтерпретації. У зв’язку з цим умови на матриці
умови не мали чіткої економічної інтерпретації. У зв’язку з цим умови на матриці 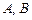 згодом були змінені, зокрема стали такими, як у наступному твердженні.
згодом були змінені, зокрема стали такими, як у наступному твердженні.
Теорема 5.15 (умови існування невиродженого положення рівноваги в моделі Неймана).Нехай невід’ємні матриці  такі, що матриця випуску
такі, що матриця випуску 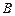 не має нульових рядків, а матриця витрат
не має нульових рядків, а матриця витрат 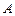 не має нульових стовпців. Тоді модель Неймана з даними матрицями має невироджене положення рівноваги, тобто система (5.53)–(5.55) має розв’язок.
не має нульових стовпців. Тоді модель Неймана з даними матрицями має невироджене положення рівноваги, тобто система (5.53)–(5.55) має розв’язок.
Умови теореми мають очевидний економічний зміст. Умова  , означає, що серед базисних процесів немає таких, які нічого не витрачають (відсутність „рогу достатку“), а умова
, означає, що серед базисних процесів немає таких, які нічого не витрачають (відсутність „рогу достатку“), а умова 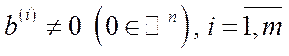 означає, що в системі (система замкнута) виробляється кожний продукт. Ці умови ще можна конкретизувати так:
означає, що в системі (система замкнута) виробляється кожний продукт. Ці умови ще можна конкретизувати так:
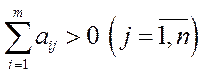 ,
, 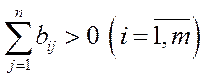 .
.
Інакше кажучи, в кожному виробничому способі використовується хоча б один продукт і кожний продукт може бути вироблений принаймні одним технологічним способом.
У процесі доведення даної теореми [1, 39] розглядається пара двоїстих задач лінійного програмування:
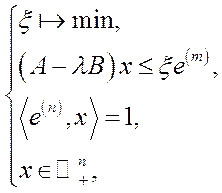 (5.56)
(5.56)
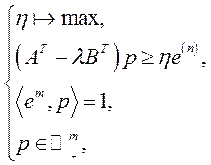 (5.57)
(5.57)
де 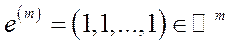 ,
, 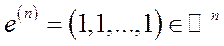 ,
, 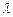 – числовий параметр.
– числовий параметр.
Установлено, що існує  , для якого
, для якого 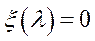 . Це означає, що для відповідного до
. Це означає, що для відповідного до 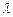 розв’язку
розв’язку 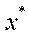 задачі (5.56), при
задачі (5.56), при 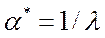 виконується співвідношення (5.53). Згідно з однією з теорем двоїстості
виконується співвідношення (5.53). Згідно з однією з теорем двоїстості 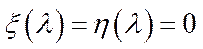 , тому для розв’язку
, тому для розв’язку 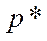 задачі (5.57) при
задачі (5.57) при 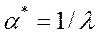 виконується співвідношення (5.54). Це означає, що знайдена трійка
виконується співвідношення (5.54). Це означає, що знайдена трійка 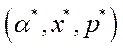 є положенням рівноваги, хоча не обов’язково невиродженим. Виявляється також, що невироджене положення рівноваги обов’язково існує. Воно гарантується в тому випадку, коли число
є положенням рівноваги, хоча не обов’язково невиродженим. Виявляється також, що невироджене положення рівноваги обов’язково існує. Воно гарантується в тому випадку, коли число  , де
, де 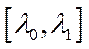 – відрізок (множина) розв’язків рівняння
– відрізок (множина) розв’язків рівняння 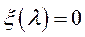
 . Функція
. Функція 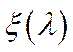 є функцією значень задачі (5.56). Ця функція визначена при всіх
є функцією значень задачі (5.56). Ця функція визначена при всіх 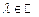 (оскільки при всіх
(оскільки при всіх  задача (5.56) має розв’язок) та володіє властивостями:
задача (5.56) має розв’язок) та володіє властивостями:
1) 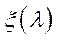 – неперервна при
– неперервна при 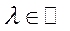 ; 2)
; 2) 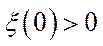 ; 3)
; 3) 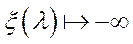 при
при 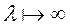 ; 4)
; 4) 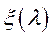 – монотонно спадна функція.
– монотонно спадна функція.
Крім того, вона має вигляд
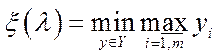 ,
,
де 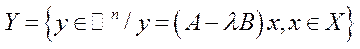 ,
, 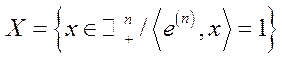 (
(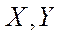 – обмежені, замкнуті множини).
– обмежені, замкнуті множини).
Означення 5.15.Числа  та
та  (найлівіший і найправіший нулі функції
(найлівіший і найправіший нулі функції 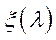 ) називаються відповідно числом Неймана і числом Фробеніуса.
) називаються відповідно числом Неймана і числом Фробеніуса.
Використовуючи наведені поняття, можна сформулювати ще одне твердження про положення рівноваги в моделі Неймана.
Теорема 5.16. Щоб трійка 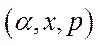 була положенням рівноваги (можливо, й виродженого) моделі Неймана, необхідно й достатньо, щоб
була положенням рівноваги (можливо, й виродженого) моделі Неймана, необхідно й достатньо, щоб 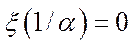 , а пари
, а пари 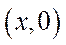 та
та  були розв’язками відповідно задач (5.56) і (5.57) при
були розв’язками відповідно задач (5.56) і (5.57) при 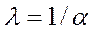 .
.
Означення 5.16. Число  , яке входить у трійку
, яке входить у трійку 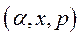 невиродженого положення рівноваги моделі Неймана
невиродженого положення рівноваги моделі Неймана 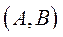 , називається темпом росту (темпом зростання замкнутої виробничої системи).
, називається темпом росту (темпом зростання замкнутої виробничої системи).
А числа 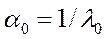 та
та 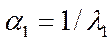 є відповідно максимально і мінімально можливими темпами росту по стаціонарній траєкторії. При
є відповідно максимально і мінімально можливими темпами росту по стаціонарній траєкторії. При 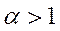 маємо розширене відтворення,
маємо розширене відтворення,
при 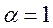 – просте відтворення, а при
– просте відтворення, а при 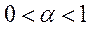 – звужене відтворення.
– звужене відтворення.
Читайте також:
- Автокореляція залишків – це залежність між послідовними значеннями стохастичної складової моделі.
- Аналіз економічноїї політики за допомогою моделі Мандела-Флемінга. Випадки вільного та фіксованого валютного курсів.
- Аналітичний підбір математичної моделі.
- Баланс сил і рівновага в МС
- Бізнес-моделювання в системі управління розвитком підприємства. Поняття та етапи формування бізнес-моделі
- Взаємодія попиту і пропозиції та ринкова рівновага.
- Взаємодія попиту і пропозиції. Ринкова рівновага.
- Взаємодія попиту й пропозиції. Ринкова рівновага
- Взаємодія попиту та пропозиції. Ринкова рівновага
- Взаємодія попиту та пропозиції: ринкова рівновага.
- Взаємозв'язок сукупного попиту та сукупної пропозиції. Макроекономічна рівновага
- Вибір підходу до процесу соціальної роботи залежить від теоретичної моделі, якої дотримуються соціальні працівники, обраної стратегії втручання і методу соціальної роботи.
| <== попередня сторінка | | | наступна сторінка ==> |
| Означення 5.5. Якщо існують похідні , то матриця | | | Продуктивність і нерозкладність моделі Неймана |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |