• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Означення 5.5. Якщо існують похідні , то матриця

,

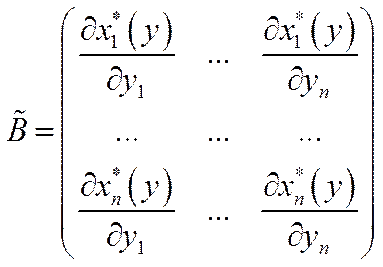називається матрицею повних стохастичних витрат.

Наступні твердження дають прості достатні умови існування матриці 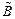і критерій стохастичної продуктивності стохастичного аналога моделі Леонтьєва.

Теорема 5.12 (про існування матриці повних стохастичних витрат для моделі (5.35)).Якщо

,

то матриця повних стохастичних витрат існує.

Теорема 5.13 (критерій стохастичної продуктивності моделі (5.35)). Щоб модель (5.35) була стохастично продуктивною, необхідно й достатньо, щоб її матриця повних стохастичних витрат 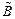була невід’ємною.

Більш детальне дослідження моделі (5.35) можна знайти у [23, 46]. Зауважимо лише, що модель (5.35) для реальних матриць , як правило, є стохастично продуктивною.

Крім моделі (5.35), можна запропонувати також інші варіанти стохастичних аналогів моделі Леонтьєва. Однак навіть цієї моделі достатньо для ілюстрації стохастичного підходу в моделюванні міжгалузевих (чи інших внутрісистемних) балансових співвідношень і з’ясування деяких проблем, пов’язаних зі стохастичною інформацією.

22. Динамічна модель міжгалузевого балансу.

Розглянуті вище моделі міжгалузевого балансу – статичні, оскільки належать до окремо взятих періодів часу й не відображають зв’язок із попередніми або наступними періодами. На відміну від статичних, динамічні моделі міжгалузевого балансу [1, 25, 39, 44, 45] враховують взаємозв’язок між попередніми й наступними періодами розвитку економіки. Інакше кажучи, динамічні моделі описують не окремий стан, а процес економічного розвитку, максимально наближаючись до реальної економічної системи. Крім того, у динамічних моделях зі складу кінцевої продукції виділяються виробничі капіталовкладення, тобто інвестиції в основний капітал, що дозволяє аналізувати їх розподіл, використання й виробничу ефективність. Нижче розглянемо варіант динамічної моделі, в основі побудови якої лежить функціональна залежність між величиною інвестицій та приростом продукції за період .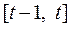

Принципова схема перших двох квадрантів динамічного міжгалузевого балансу (ДМБ) наведена в таблиці 5.5.

Читайте також:

1. Блочна матриця.
2. Будучи, як правило, дочірніми фірмами великих компаній, вони існують за рахунок засобів венчурного капіталу і здійснюють чітко визначений вид діяльності.
3. Види прийомів, які існують в міжнародній практиці
4. Границя функції. Означення границі функції за Гейне й за Коші.
5. Графічне позначення матеріалу в перерізах і на виді - штрихування, що виконується тонкими суцільними лініями.
6. Дiї над матрицями
7. Дайте характеристику соціальної політики української держави в умовах ринкової економіки. Які існують проблеми, труднощі? Які ви бачите шляхи їх вирішення?
8. Дайте характеристику соціальної політики української держави в умовах ринкової економіки. Які існують проблеми, труднощі? Які ви бачите шляхи їх вирішення?
9. Два означення інтегралу. Теореми про загальний вигляд інтегралу та залежність двох інтегралів одного диференціального рівняння.
10. Демократія - це така форма організації та функціонування політичної системи, при якій існують рівні можливості для здійснення прав і свобод кожного члена суспільства.
11. Дії над матрицями
12. Дії над матрицями

Переглядів: 749