• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Співвідношення (4.39), (4.40) називають законом Вальраса в широкому розумінні, а (4.36), (4.40) – законом Вальраса у вузькому розумінні.

У розгорнутому вигляді умови (4.38)–(4.40) мають вигляд:

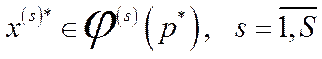, (4.41)

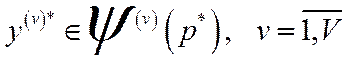, (4.42)

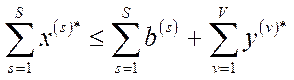, (4.43)

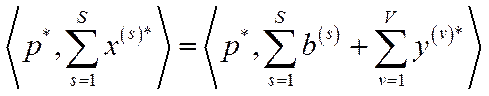. (4.44)

Отже, модель ринку за Вальрасом побудована. Умови рівноваги задаються співвідношеннями (4.38)–(4.40) або
(4.41)–(4.44). Процес формування ринкових цін можна реалізувати за допомогою алгоритму, який складається з чотирьох блоків (рис. 4.4.).

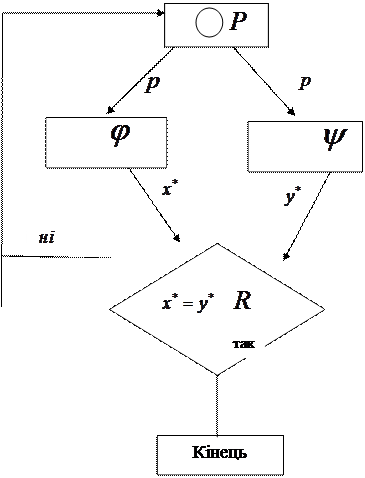
У блоці 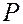формується вектор цін 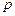. Після цього інформація про вибрані ціни надходить до блоків 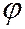і 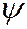, у яких формуються множини 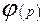і 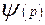, інформація про які надходить у блок 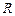попарного порівняння елементів 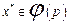і 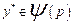. Якщо 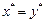, то процес формування рівноважних цін на цьому закінчується. Якщо це не так, то повертаємось у блок 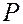і продовжуємо процедуру до тих пір, поки не будуть знайдені рівноважні ціни.

Реалізація даного алгоритму пов’язана з двома фундаментальними проблемами:

· установлення факту існування конкурентної рівноваги в моделі Вальраса;

· розробка збіжного до рівноважних цін обчислювального алгоритму.

У найбільш загальному випадку існування конкурентної рівноваги в моделі Вальраса не встановлено, оскільки така модель досить абстрактна. Однак факти існування рівноваги встановлені для різних модифікацій моделі Вальраса, зокрема для моделі Ерроу-Дебре. Успішна розробка збіжних алгоритмів ґрунтується на використанні конструктивних необхідних і достатніх ознак рівноваги.

За теоремою Ерроу-Дебре, конкурентна рівновага в моделі Вальраса існує, якщо виконуються такі умови:

1. Множина наборів споживчих благ 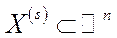для споживача – це замкнена, опукла і необмежена множина .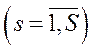

2. Множина 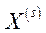має нижню межу, тобто існує вектор 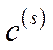, для якого , .

3. Функція неперервна й угнута на .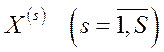

4. Кожний споживач 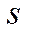ненасичуваний, тобто в 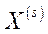немає точки насичення – найбільш переважного елемента (споживач завжди віддасть перевагу більшому набору товарів перед меншим) і володіє додатною початковою власністю .

5. Кожна технологічна множина 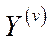– це замкнена опукла множина .

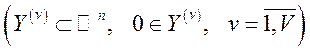6. Сукупна технологічна множина – опукла і задовольняє умову 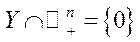, тобто не може існувати додатного чистого випуску хоча б по одному з товарів без існування хоча б по одному з товарів (ресурсу) від’ємних затрат.

7. Існують такі 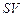констант 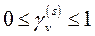, , 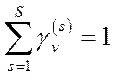, 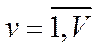що 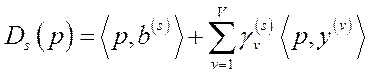, тобто 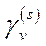– частка участі -того споживача в прибутку виробника 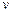(ця умова означає, що прибуток кожного виробника повністю розподіляється між споживачами-пайовиками).

На закінчення підкреслимо, що існування конкурентної рівноваги не означає, що економіка перейде в цей стан.
У випадку, коли такий перехід можливий, потрібно розробити його відповідний алгоритм.

18. Схема міжгалузевого балансу. Модель Леонтьєва. Аналіз продуктивності моделі Леонтьєва.

Перші варіанти моделей міжгалузевих балансів розроблені ще у 20-30 рр. ХХ ст. Наукові результати в розробці таких моделей пов’язані з іменем видатного американського економіста В.В. Леонтьєва. Вивчення моделі Леонтьєва почнемо з конкретизації схеми міжгалузевого балансу (СМБ) виробництва й розподілу суспільного продукту.

Нехай для економічної системи (економіки країни, регіону тощо), яка представлена сукупністю окремих галузей (видів виробництва), виконуються такі припущення:

· в економіці функціонує 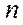галузей;

· уся вироблена валова продукція поділяється на проміжну й кінцеву;

· кожна галузь виробляє єдиний макропродукт єдиним технологічним способом.

Встановлено, що для формалізації схеми МБ економісти будують міжгалузеві баланси в одній із трьох форм:

· натуральній;

· натурально-вартісній;

Галузі- виробники	Галузі-споживачі	Кінцева продукція	Валова продукція
		...
			...
			...
...	...	...	...	...	...	...
			...
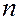
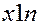
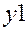
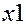
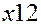
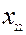
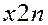
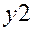
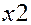
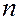
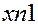
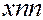
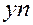
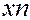
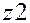
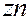
Умовно чиста продукція			...		IV
Валова продукція			...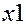

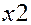
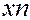
· вартісній.

У економіко-математичних дослідженнях найбільш зручна вартісна форма балансу, коли все вимірюється у відносних одиницях виміру.

СМБ складається з чотирьох блоків (квадратів).

Перший квадрант конкретизує матрицю 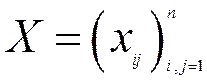міжгалузевих потоків продукції. Елемент 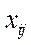– це кількість продукції 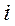-тої галузі, яка споживається 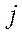-тою галуззю в процесі її функціонування за певний період часу (для якого складається баланс).

Другий квадрант характеризується кінцевою продукцією невиробничого споживання, яка включає в себе приріст запасів, особисте споживання населення, витрати на утримання державного апарату, оборону, освіту, медицину тощо. Очевидно, що валова продукція кожної 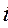-тої галузі-виробника 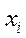складається з проміжної (продукції виробничого споживання) та кінцевої продукції 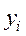, тобто 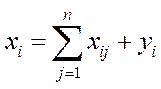, 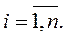(5.1)

Третій квадрант описує вартісну структуру валової продукції, яка для поділена на продукцію виробничого споживання та умовно чисту продукцію , і складається з окремих компонентів і виконуються такі співвідношення:

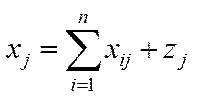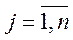, , (5.2)

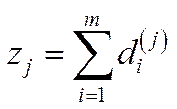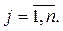, (5.3)

Четвертий квадрант вільний. У ньому здебільшого відображається розподіл і використання умовно чистої продукції чи національного доходу.

Просумувавши (5.1) і (5.2) та врахувавши, що 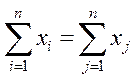, отримаємо співвідношення

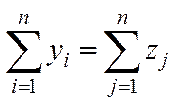. (5.4)

Ця рівність показує, що сумарна кінцева продукція завжди дорівнює сумарній умовно чистій продукції або це означає, що в міжгалузевому балансі виконується принцип еквівалентності матеріального та вартісного складу національного доходу.

Формалізація моделі Леонтьєва

У міжгалузевому балансі технологічні зв’язки між галузями визначаються коефіцієнтами прямих матеріальних витрат

, , , (5.5)

які показують витрати продукції 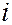-тої галузі на виробництво одиниці продукції 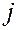-тої галузі з урахуванням лише прямих витрат.
З урахуванням (5.5) співвідношення (5.1) набувають вигляду

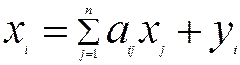, (5.6)

або в матрично-векторній формі

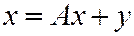, (5.7)

де та 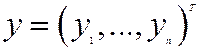– відповідно вектори валової й кінцевої продукції, а матриця 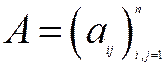– матриця коефіцієнтів прямих матеріальних витрат.

Систему (5.7) прийнято називати статичною моделлю Леонтьєва. Якщо матриця задана, а вектори та – невідомі, то (5.7) чи (5.6) є системою 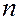лінійних алгебраїчних рівнянь з 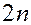невідомими.

У зв’язку з цим проблему існування вектора 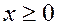(0 – 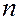-вимірний нульовий вектор), який є розв’язком системи (5.7) при 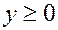, називають проблемою продуктивності моделі Леонтьєва.Інакше кажучи, проблема продуктивності рівносильна проблемі існування оберненої матриці 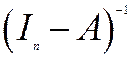, де 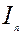– діагональна одинична матриця розмірності 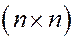або проблемі існування непорожньої множини:

,

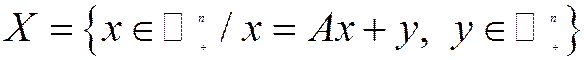де 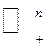– невід’ємний ортант 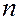-вимірного векторного простору.

Якщо продуктивність моделі Леонтьєва встановлена, то із (5.7) випливає, що

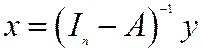. (5.8)

Формула (5.8) конкретизує шуканий розв’язок моделі Леонтьєва. При цьому матрицю 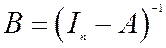називають матрицею повних матеріальних витрат (елемент 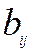– це кількість продукції 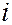-тої галузі, яка необхідна для випуску одиниці кінцевої продукції 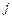-тої галузі з урахуванням як прямих, так і опосередкованих (непрямих) витрат).

Матриця 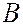також невід’ємна, це випливає з рівності

.

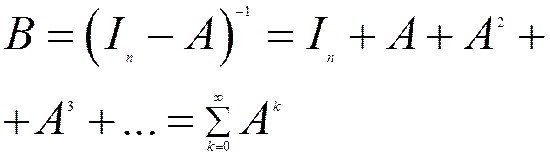У теорії міжгалузевих балансів чітку економічну інтерпретацію має також матриця непрямих матеріальних витрат 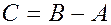, що також складається з невід’ємних елементів.

Елемент 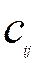– це кількість опосередкованих витрат продукції 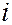-тої галузі для виробництва одиниці продукції 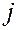-тої галузі.

Крім системи (5.6) чи (5.7) розглядають також двоїсту до неї систему, яка записується в термінах цін.

Нехай 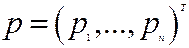– вектор цін (інколи вектор називають вектором індексів зростання цін), кожна компонента 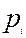якого є ціною одиниці продукції -тої галузі. Якщо елементи І і ІІІ квадрантів таблиці 5.1 записані у натуральній формі, з урахуванням цін І і ІІІ квадранти міжгалузевого балансу можна відобразити у таблиці 5.2.

Таблиця 5.2

Галузі- виробники	Галузі-споживачі
		...
			...
			...
...	...	...	...	...
			...
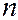
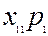
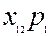
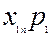
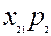
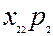
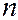
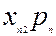
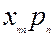
Умовно чиста продукція			...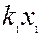
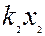
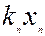
Валова продукція			...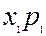

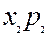
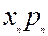
Із таблиці 5.2. випливають балансові співвідношення

,

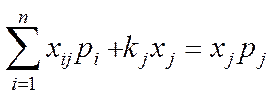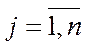
або

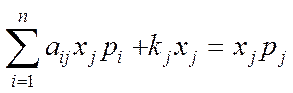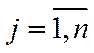, , (5.9)

де 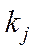– коефіцієнт умовно чистої продукції галузі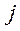 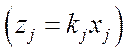або відносна ціна одиниці продукції 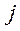, яка включена в умовно чисту продукцію.

Співвідношення (5.9) називають двоїстою моделлю до моделі (5.6).

Вектор можна записати ще у такому вигляді:

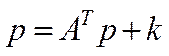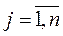, , (5.10)

де .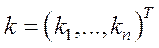

Співвідношення (5.10) також називають двоїстою моделлю до моделі (5.7).

Система (5.10) чи (5.9) прибуткова, якщо вона має додатний розв’язок . Можна довести, що прибутковість системи (5.10) і продуктивність системи (5.7) еквівалентні: із продуктивності прямої системи випливає прибутковість двоїстої та навпаки.

Отже, моделі міжгалузевого балансу дозволяють кількісно оцінити на прогнозний період рівень цін у галузях економіки.

Дослідження продуктивності моделі Леонтьєва

Математичний аналіз моделі Леонтьєва пов’язаний із теорією невід’ємних матриць. Невід’ємні матриці можна поділити на два класи: розкладні та нерозкладні. З’ясуємо зміст цих понять.

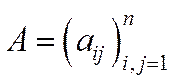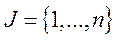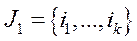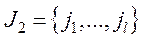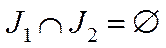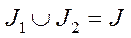
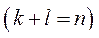Означення 5.1. Невід’ємна матриця називається розкладною, якщо множину індексів можна розбити на такі дві підмножини: , , що , та , , .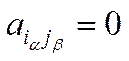

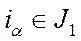Усі інші невід’ємні матриці називаються нерозкладними.

Підмножини 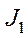та 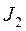ще називають ізольованими. Якщо перенумерувати індекси так, щоб , а 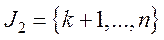, то для матриці це означає одночасну перестановку рядків і стовпчиків. Така операція дозволяє звести матрицю 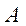до вигляду

,

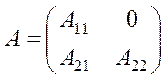де і 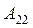– квадратні матриці.

Наприклад, якщо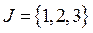, , , то матриця

,

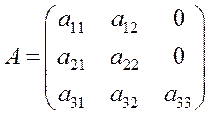очевидно, розкладна 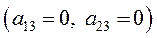. При цьому

, , , .

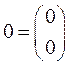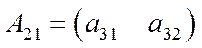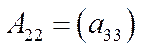З іншого боку, матриця

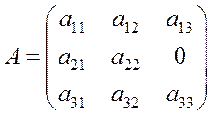
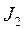нерозкладна, бо немає таких ізольованих підмножин та , щоб , , .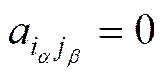

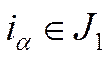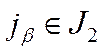Основні властивості нерозкладних матриць.

· Нерозкладна матриця не може мати ні нульових рядків, ні нульових стовпців.

· Якщо матриця нерозкладна, а вектор , то .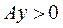

· Якщо – нерозкладна матриця розмірності 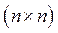, то 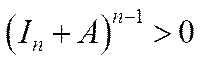, тобто всі елементи матриці 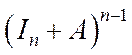додатні.

· Якщо 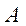– нерозкладна, то для будь-якої пари індексів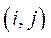 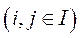існує натуральне число 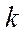, для якого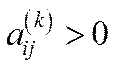
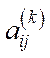(– елемент матриці ).

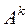· Для того, щоб матриця 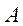була нерозкладною, необхідно й достатньо, щоб для будь-яких індексів 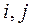існувала послідовність 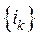, , 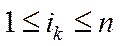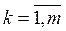така, що , , , .

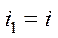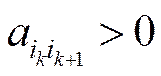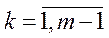· Якщо матриця 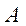нерозкладна, а 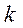– довільне натуральне число, то в матриці 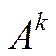не може бути ні нульових рядків, ні нульових стовпців.

Розкладність і нерозкладність мають чітку економічну інтерпретацію. Розкладність матриці прямих матеріальних витрат 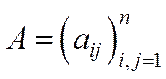означає, що існує група ізольованих галузей, які можуть функціонувати незалежно від інших галузей. У випадку нерозкладності цієї матриці такої групи галузей не існує.

Щоб сформулювати необхідні та достатні умови продуктивності моделі Леонтьєва, наведемо деякі факти з теорії невід’ємних матриць.

Теорема 5.1 (Теорема Перрона-Фробеніуса про спектральні властивості невід’ємної нерозкладної матриці).Нехай 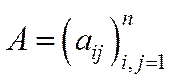– невід’ємна нерозкладна квадратна матриця, а 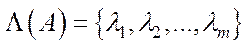, 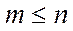– множина її власних значень. Тоді в множині 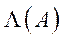є таке власне значення , що , , 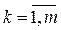і якому відповідає єдиний (з точністю до скалярного множника) власний вектор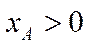 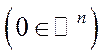. При цьому число 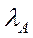називають числом Фробеніуса, а вектор 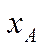– вектором Фробеніуса матриці .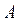

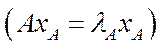Вектор 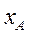ще називають правим вектором Фробеніуса, оскільки існує також вектор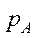 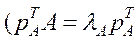або 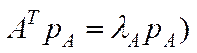, який називають лівим вектором Фробеніуса. У випадку нерозкладності матриці 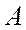, транспонована матриця 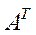теж буде нерозкладною.

Теорема 5.2 (про спектр довільної невід’ємної матриці). Нехай 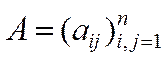– невід’ємна квадратна матриця,
а 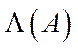– множина її власних значень. Тоді в множині 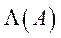є таке власне значення 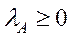, що , 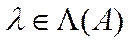і якому відповідає власний вектор .

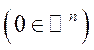Теорема 5.3 (про оцінки для фробеніусівського числа невід’ємної матриці). Нехай 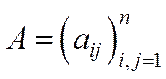– невід’ємна квадратна матриця. Тоді для її фробеніусівського числа 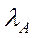справджуються такі оцінки:

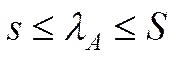, , (5.11)

де , , , ,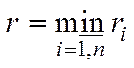

, .

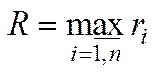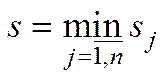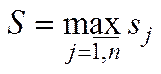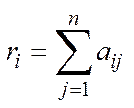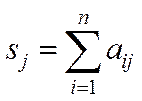Якщо матриця 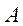ще й нерозкладна, то нерівності (5.11) строгі, за винятком випадку , .

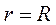Теорема 5.4 (критерій продуктивності моделі Леонтьєва). Для продуктивності моделі Леонтьєва з невід’ємною нерозкладною матрицею необхідно і достатньо, щоб фробеніусівське власне число 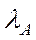даної матриці задовольняло нерівність .

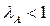Отже, перевірка на продуктивність зводиться до суто математичної задачі щодо спектра матриці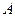. У загальному випадку така задача досить складна, тому широкого практичного застосування цей критерій продуктивності моделі Леонтьєва не отримав. У зв’язку з цим розроблені значно простіші достатні умови продуктивності.

Теорема 5.5 (достатня умова продуктивності моделі Леонтьєва). Якщо система 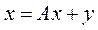має розв’язок 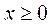при деякому , то модель Леонтьєва продуктивна. Інакше кажучи, якщо в моделі Леонтьєва можна задовольнити деякий додатний вектор кінцевої продукції, то модель продуктивна.

Теорема 5.6 (достатні умови продуктивності моделі Леонтьєва). Якщо матриця 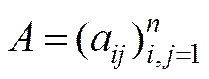невід’ємна та нерозкладна, а

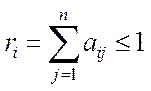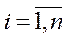, , (5.13)

і хоча б для одного рядка 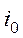виконується нерівність , то модель Леонтьєва, яка відповідає цій матриці, продуктивна.

19. Коефіцієнт трудових витрат і витрат виробничих фондів

Коефіцієнти трудових витрат та витрат виробничих фондів служать для побудови деяких модифікацій моделей МБ та економіко-математичного аналізу балансових співвідношень.

Нехай у економіці, яка має 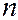галузей 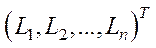– вектор трудових ресурсів, а 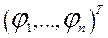– вектор виробничих фондів у 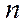галузях економіки.

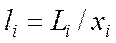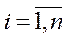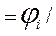
Величини , , будемо називати коефіцієнтами прямих трудових витрат, а величини 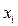, , 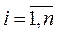– коефіцієнтами прямих витрат виробничих фондів (коефіцієнтами фондомісткості одиниці -тої продукції).

Повні трудові витрати визначаються величиною

(5.13),

де 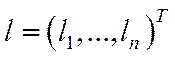буде називатись вектором повних витрат трудових ресурсів, 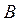– матриця повних матеріальних витрат у міжгалузевому балансі, – вектор кінцевої продукції. Аналогічно обчислюються повні витрати виробничих фондів

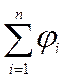
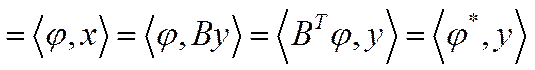(5.14)

Компоненти вектора 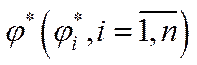називаються коефіцієнтами повних витрат виробничих фондів (витрат фондів на одиничні кінцеві випуски).

Зазначимо, що коефіцієнти трудових витрат та витрат виробничих фондів мають важливе значення для кількісного та якісного економічного аналізу міжгалузевих зв’язків.

Введені вище коефіцієнти витрат трудових ресурсів та виробничих фондів використовуються для побудови деяких модифікацій МБ та економіко-математичного аналізу балансових співвідношень.

Перш ніж сформулювати так звану оптимальну модель розподілу ресурсів у 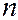галузевій економіці, зазначимо, що основною причиною побудови такої моделі є наперед відомі загальні витрати трудових ресурсів у даній економіці. Це означає, що відома величина 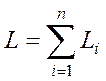. У цьому випадку ставити задачу про знаходження вектора валового випуску 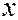, який би був розв’язком моделі Леонтьєва при будь-якому заданому 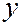не доцільно, оскільки наявних трудових ресурсів може не вистачити для досягнення .

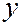Очевидно, що балансові співвідношення між валовим кінцевим випуском потрібно доповнити обмеженням: .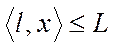

Оскільки часто при плануванні кінцевого випуску задають його структуру, то нехай 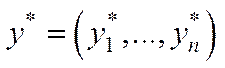- це і є той базовий вектор кінцевої продукції, який визначає її структуру. Тоді можна розв’язувати задачу про максимізацію числа комплектів кінцевої продукції 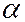при наявних обмеженнях на валову та кінцеву продукцію і трудові ресурси. Така задача може бути формалізована у вигляді:

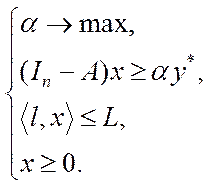(5.16)

З одного боку (5.16) є моделлю максимізації кінцевого випуску, а з іншого – моделлю оптимального розподілу трудових ресурсів. Аналогічно формується модель оптимізації числа комплектів кінцевої продукції при відповідних балансових обмеженнях на валову та кінцеву продукції та витрати на виробничі фонди. Дана модель має вигляд:

(5.17)

Модель (5.17) також є моделлю оптимального розподілу ВФ. Якщо до моделей (5.16) та (5.17), які є задачами лінійного програмування, виписати двоїсті задачі та скористатись І та ІІ основними теоремами двоїстості, то можна здійснити економіко-математичний аналіз процесів, пов’язаних з моделлю Леонтьєва та трудовими ресурсами.

20. Порівняльна статика моделі Леонтьєва.

Використовуючи модель Леонтьєва, вивчимо реакцію виробничої системи з технологічною матрицею 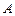на зміну вектора кінцевої продукції 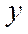. Усі компоненти вектора 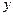є в даному випадку екзогенними параметрами. Результати досліджень сформулюємо й обґрунтуємо у вигляді строгих математичних тверджень.

Теорема 5.9 (про додатність вектора валового випуску в моделі Леонтьєва з невід’ємною, нерозкладною й продуктивною матрицею).Якщо в моделі (5.7) матриця 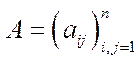невід’ємна, нерозкладна й продуктивна, а вектор 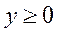, 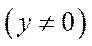то вектор валового випуску буде додатним: .

Доведення. Оскільки 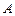– продуктивна матриця, то 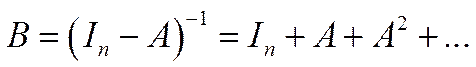, тобто

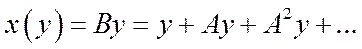(5.27)

Крім того, згідно з однією з властивостей нерозкладних матриць для будь-якої пари індексів 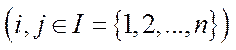, існує таке натуральне числ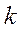о , що 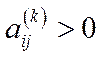(– елемент матриці 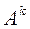). Це означає, що 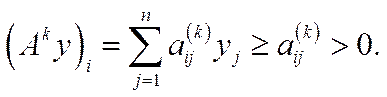Отже, із (5.27) випливає, що для всіх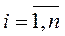

.

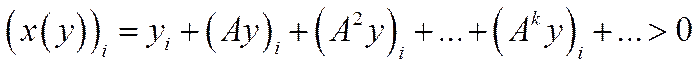Отже, додатність вектора валового випуску встановлена.

Зауважимо також, що в умовах теореми 5.9 матриця .

Тепер з’ясуємо питання про те, як зміниться вектор валового випуску 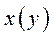, якщо попит на перший товар (тобто перша координата вектора 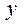) збільшиться.

Теорема 1. Нехай в моделі (5.7) матриця 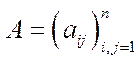– невід’ємна, нерозкладна і продуктивна, а вектор 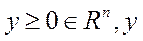тотожно не дорівнює 0. Тоді вектор валового випуску .

Теорема 2. Нехай в моделі (5.7) матриця 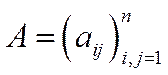– невід’ємна, нерозкладна і продуктивна. Якщо 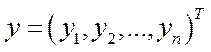, , причому 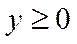, , 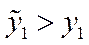то

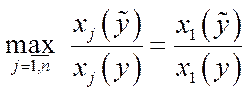. (5.28)

Якщо

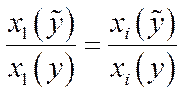(5.29)

при 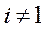, то .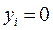

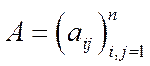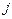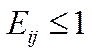
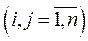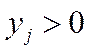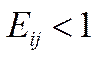Теорема 3. Якщо матриця – невід’ємна, нерозкладна й продуктивна, то еластичність будь-якого валового продукту і відносно попиту на довільний кінцевий продукт не перевищує одиниці: . Якщо ж , то при .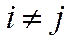

21. Стохастичний аналог моделі Леонтьєва.

Розглянута раніше модель Леонтьєва є статичною, однозначно визначеною. На практиці в більшості випадків матриця А є продуктивною, тобто не виникає проблем із знаходженням розв’язку моделі Леонтьєва, який у матричному вигляді записується так:

Як правило, модель Леонтьєва (5.7) використовується для прогнозування вектора валового випуску 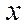при заданому векторі кінцевої продукції 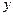. Проблема існування шуканого вектора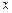, тобто проблема продуктивності моделі, є основною при розв’язанні цієї задачі. У більшості випадків реальна матриця 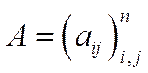така, що 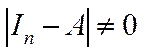, тому існування єдиного невід’ємного розв’язку 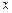системи (5.7) (чи (5.6)) забезпечується невід’ємністю матриці .

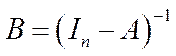Ситуація змінюється, якщо матрицю 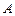вважати випадковою (внаслідок помилок вимірювання та прогнозування), тобто вважати, що кожний її елемент 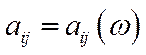є випадковою величиною або дійсною числовою функцією, заданою на множині елементарних подій 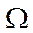, яка є елементом імовірнісного простору 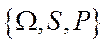, де 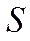– так звана
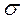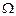– алгебра подій, а – імовірнісна міра, визначена на і 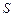(згідно з визначенням випадкової величини для будь-якого 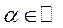, виконується умова 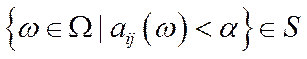та існує ймовірність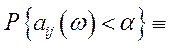 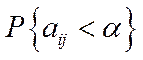, яка дорівнює конкретному значенню функції розподілу 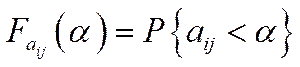,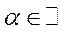). Якщо матриця прямих матеріальних витрат випадкова, то реальний випуск кінцевої продукції 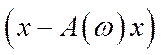буде випадковим вектором і лише в рідкісних випадках він може збігатись із плановим вектором 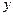(для детермінованого випадку 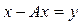), тому досягти балансу в традиційному розумінні неможливо. Це означає, що випуск валової продукції потрібно вибирати так, щоб мінімізувати похибку апріорного відхилення. Реалізувати цей вибір можна, наприклад, мінімізуючи математичне сподівання суми квадратів відхилень, тобто розв’язуючи задачу стохастичного програмування

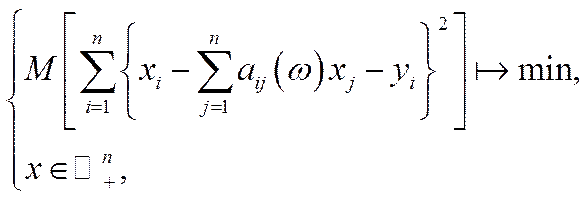(5.35)

де – математичне сподівання. Задача (5.35) є задачею стохастичного програмування в так званій 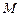-постановці, при якій випадкова величина замінюється її математичним сподіванням, і задача зводиться до оптимізації детермінованої цільової функції. Не зупиняючись на методах розв’язування задачі (5.35), зазначимо лише, що вона формалізує один із можливих стохастичних аналогів моделі Леонтьєва [5, 19, 23]. Стосовно (5.35) вводиться також поняття стохастичної продуктивності.

Означення 5.4. Модель (5.35) називається стохастично продуктивною, якщо вона має розв’язок при будь-якому .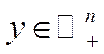

З поняттям стохастичної продуктивності тісно зв’язано поняття повних стохастичних витрат валової продукції (в детерміновану випадку такий зв’язок є між продуктивністю та повними витратами валової продукції). Якщо вектор 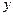в задачі (5.35) є сукупністю параметрів, то її розв’язок буде вектор-функцією .

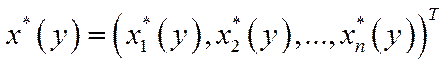Читайте також:

1. II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
2. IV. Закономірності структурно-функціональної організації спинного мозку
3. Алкени – вуглеводні, в молекулах яких є один подвійний зв’язок між атомами вуглецю . Алкені називають також олефінами або етиленовими вуглеводнями.
4. Алкіни – вуглеводні, в молекулах яких є два атоми вуглецю, сполучені потрійним зв’язком - -. Алкіни називають також ацетиленовими вуглеводнями.
5. Аналіз співвідношення активів із джерелами їх фінансування
6. Будова і закономірності розвитку крайових прогинів
7. Бюджетні установи отримують кошти на своє функціонування з бюджету виключно на основі фінансових документів, які називаються кошторисами.
8. Вади розвитку – це порушення внутрішньоутробного розвитку, відхилення від нормальної будови організму. Найлегші ступені вад розвитку називають аномаліями, найважчі – потворністю.
9. Варіанти співвідношення потреб і виробництва
10. Взаємозалежність і співвідношення громадянського суспільства і правової держави.
11. Взаємозалежність і співвідношення громадянського суспільства і правової держави.
12. Види інноваційних стратегій та їх співвідношення

Переглядів: 1103