Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Гіпотеза де-Бройля

КВАНТОВА МЕХАНІКА

Хвильові властивості речовини. В 1924 р. де-Бройль висунув гіпотезу, що двоякість (дуалізм) не є особливістю тільки світла, але має універсальне значення. Він припустив, що частинки речовини поряд з корпускулярними властивостями мають також і хвильові і переніс на випадок частинок речовини ті ж правила переходу від корпускулярної картини до хвильової, які справедливі для світла. Ці твердження отримали назву гіпотези де-Бройля. Фотон має енергію і імпульс

e=հn, p=հ/l .

Енергія і імпульс відбивають його корпускулярні властивості, а частотаn і довжина l – хвильові властивості.

За ідеєю де-Бройля рух будь-якої частинки пов’язаний з поширенням хвилі, довжина якої

l=հ/р (8.1)

а частота – n=e/հ.

Ці хвилі спочатку називали хвилями де-Бройля, а потім вони отримали назву хвилі матерії. Гіпотезу де-Бройля невдовзі було блискуче підтверджено експериментально у досліді з проходження електронного пучка через металеву фольгу (див. рис. 88, а).

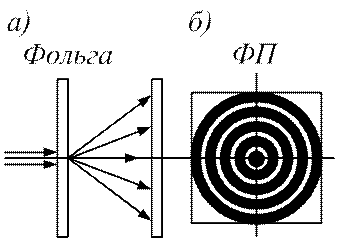
Рис. 88

Прискорений пучок електронів проходить через тонку металеву фольгу і потрапляє на фотопластину (ФП). Електрон при співударі з фотопластиною чинить на неї таку ж дію, як фотон, тобто засвітлює місце попадання. Пучок електронів розсіюється металевою фольгою і дає дифракційну картину, аналогічну до тієї, що має місце при падінні на фольгу рентгенівського

випромінювання (див. рис. 88, б). При цьому дифракційна картина відповідає довжині хвилі

l=հ / mv,

де v – швидкість електронів, тобто збігається з довжиною хвилі де-Бройля з формули (8.1).

Таким чином, матерія двояка, тобто частинки речовини одночасно мають і корпускулярні і хвильові властивості. Це положення називається принципом двоякості.

§2. Квантово-механічний опис руху мікрочастинок

Виникла потреба побудувати механіку, яка б враховувала хвильові властивості частинок. Ця механіка спочатку отримала назву хвильової, а потім квантової механіки.

Рівняння Шредінгера. Основним рівнянням квантової механіки є рівняння Шредінгера. Для стаціонарних станів тобто станів, що не змінюються у часі, рівняння Шредінгера має вигляд

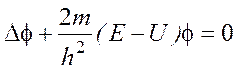де Δ=д²/дx²+д²/дy²+д²/дz² – оператор Лапласа (лапласіан);

m – маса частинки;

U –потенціальна енергія частинки у силовому полі, в якому вона рухається;

E – повна енергія частинки;

f (x,y,z ) – хвильова функція.

Хвильова функція. У квантовій механіці стан частинки описується хвильовою функцією f (x,y,z). Фізичний зміст хвильової функції полягає в тому, що квадрат її модуля визначає густину ймовірності знаходження частинки у відповідному місці простору. Тоді імовірність dP того, що частинка буде знайдена у межах об’єму dV визначається формулою

dP=|f|²dV.

Співвідношення невизначеностей. Квантова механіка має статистичний характер. Вона не дозволяє визначити місцезнаходження частинки у просторі або траєкторією, по якій рухається частинка. У застосуванні до мікрочастинок поняття певного місцеположення і траєкторії взагалі відсутні, оскільки рух по певній траєкторії не сумісний з хвильовими властивостями частинок.

Ступінь точності, з якою до частинки можна застосувати уявлення про певне положення її у просторі, дається співвідношенням невизначеностей. Згідно з цим співвідношенням частинка не може одночасно мати точне значення координати і відповідне цій координаті значення імпульсу. Математичне формулювання цього принципу має вигляд

Δx·Δp_x≥ ħ,

де Δx – невизначеність (абсолютна похибка) координати; Δp_x– невизначеність імпульсу вздовж цієї координати.

Із співвідношення невизначеностей випливає, що чим точніше визначена одна з величин (координата або імпульс уздовж цієї координати), тим більшою стає невизначеність (похибка) іншої величини.

Квантування. Відповідно до свого фізичного змісту хвильова функція f (x,y,z) повинна бути однозначною, кінцевою і безперервною у всій області визначення x,y,z. Рівняння Шредінгера має рішення, яке задовольняє цим умовам, не при будь-яких значеннях енергії Е, а лише при певних визначених значеннях. Отже, енергія частинки у заданому силовому полі квантована, тобто змінюється не безперервно, а дискретно квантами (порціями) енергії з певним для даного силового поля (яке описується потенціальною енергією U) законом квантування. Крім енергії частинки, виявляються квантованими і інші її характеристики (момент імпульсу, тощо).

§3. Атом водню

Енергія атома. В атомі водню потенціальна енергія

U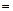–Ze²/r,

де е – заряд електрона, r – відстань електрона від ядра, Z – ціле число.

Якщо Z=1 – це атом водню, а при Z ≠ 1 – воднеподібний атом, тобто атом будь-якого елемента в якого відщеплені всі електрони, крім одного.

Рівняння Шредінгера для стаціонарних станів воднеподібного атому

Δf+2m(E+Ze²/r)f/ħ²=0

має розв’язок в наступних випадках:

1) При будь-яких позитивних значеннях енергії електрона Е. Цей випадок відповідає електрону, що пролітає поблизу ядра і йде знову на нескінченність (див. рис. 89).

Рис. 89

2) При дискретних від’ємних значеннях. Цей випадок відповідає електрону, що знаходиться у межах атому. Енергія електрона при цьому визначається формулою

(n=1,2,3…).

Квантові числа. Хвильові функції f_n,l,m, що відповідають значенням енергії Е_n, містять три цілочисельні параметри:

1) n – головне квантове число, яке приймає цілочисельні значення n=1, 2, 3…;

2) l – азимутальне квантове число, яке при заданому головному числі n приймає цілочисельні значення l=0,1,2,3,..,n–1 – всього n значень;

3) m – магнітне квантове число, яке при заданому азимутальному числі l приймає цілочисельні значення m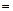–l,…,0,…+l. – всього 2l+1 значень.

Таким чином, кожному значенню енергії Е_n відповідає кілька хвильових функцій f_n,l,m, що відрізняються квантовими числами l і m. Стани з однаковою енергією називаються виродженими. Кратність виродження дорівнює

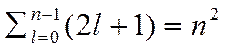Азимутальне квантове число l визначає орбітальний, тобто пов’язаний з рухом по орбіті навколо ядра, момент імпульсу електрона в атомі. Закон квантування моменту імпульсу електрона .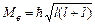

Магнітне квантове число m визначає проекцію орбітального моменту імпульсу на вектор 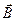магнітного поля. Закон квантування .

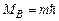Таким чином, орбітальний момент імпульсу електрона в атомі і його проекція на напрямок магнітного поля, як і енергія, є квантовими числами, тобто змінюються дискретно кожна відповідно до свого закону квантування.

У атомній фізиці стан електрона в атомі з різними значеннями азимутального квантового числа прий-нято позначати літерами.

l=0 – s-стан,

l=1 – p-стан,

l=2 – d-стан,

l=3 – f-стан.

Потім g, h і далі за латинською абеткою. Наприклад, якщо стан електрона 3p, то це означає, що n = 3, l = 1.

Переходи електронів за енергетичним спектром. Схему рівнів енергії (енергетичний спектр) зручно приставити у вигляді, що подано на рис. 90.

Рис. 90

Випромінювання і поглинання енергії атомом водню відбувається при переходах електрона із стану з одним значенням енергії Еn у стан з іншим значенням енергії (коротко кажуть – при переходах електрона з одного енергетичного рівня на інший).

Можливі тільки такі переходи, для яких азимутальне квантове число l змінюється на одиницю:

Δ l=±1. (8.2)

Умова (8.2) називається правилом відбору і є наслідком закону збереження моменту імпульсу при випромінюванні і поглинанні фотона.

Спектри випромінювання і поглинання. Переходи np®1s (n=2,3…) утворюють серію ліній випромінювання, яка називається серією Лаймана. Переходи електрона ns®2p, nd®2p, np®2s (n=3,4…) утворюють серію ліній випромінювання, яка називається серією Бальмера. Стан 1s – стан з мінімальною енергією – називається основним станом.

Атом поглинає (і випромінює) тільки ті фотони, енергія яких точно відповідає різниці енергії двох його рівнів. Спектр поглинання (з основного стану) 1s®np (n=2,3…).

§4. Багатоелектронні атоми

В атомах, що містять кілька електронів, кожний з електронів рухається в усередненому полі ядра і решти електронів. Енергетичні рівні електрона в такому центрально симетричному полі залежать не тільки від головного квантового числа n, але і від азимутального l, а відповідні їм хвильові функції від трьох квантових чисел

E=E_nl , f=f_nlm,

тобто в цьому випадку знімається виродження за азимутальним квантовим числом l.

Момент імпульсу атома в цілому складається з моментів імпульсу електронів, що входять до складу атома. Додавання моментів імпульсу здійснюється за квантовими законами

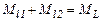де 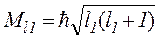; – моменти імпульсів, що додаються, l₁, l₂– їх азимутальні квантові числа. При цьому результуючий момент імпульсу

де L=l₁+l₂, l₁+l₂–1,…..½l₁–l₂½ – азимутальне квантове число результуючого моменту імпульсу. Таким чином, результуючий момент імпульсу може набувати 2l₂+1 або 2l₁+1 (потрібно взяти менше з l_i ) різних значень.

Переходи в енергетичній схемі рівнів атома підкоряються такому правилу відбору: можливі лише такі переходи, при яких момент імпульсу атома змінюється на одиницю .

§5. Спін електрона

Якщо атоми, що випромінюють світло, помістити у магнітне поле, то лінії випромінювання в спектрі випромінювання цього атома розщеплюються на кілька окремих лінії – мультиплет. Для пояснення мультиплетної структури спектрів у 1925 р. була висунута гіпотеза про те, що електрон має власний момент імпульсу M_s, не пов’язаний з рухом електрона по орбіті. Цей власний момент імпульсу електрона було названо спіном. Спін слід вважати внутрішньою властивістю, яка притаманна електрону, подібно тому, як йому притаманні заряд і маса.

Величина власного моменту імпульсу мікрочастинки визначається квантовим числом s

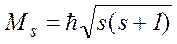Для електрона S =1/2; .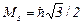

Проекція спіна на напрямок вектора індукції 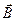магнітного поля

де спінове квантове число електрона .

Повний момент імпульсу M_j електрона в атомі складається з орбітального M_e і спінового M_s .

M_j =M_e + M_s,

де .

При цьому квантове число j, що визначає повний момент імпульсу електрона при , приймає два значення

а при l=0 тільки одне значення .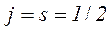

З механічними моментами пов’язані магнітні моменти, які взаємодіють один з одним подібно до того, як взаємодіють два контури з струмом. Енергія цієї взаємодії (яка називається спін-орбітальною взаємодією) залежить від взаємної орієнтації орбітального і спінового моментів. Отже, стани з різними квантовими числами j повинні мати різні енергії, і тому лінії випромінювання розщеплюються на мультиплети.

§6. Розподіл електронів в атомі по енергетичних рівнях

Таким чином, стан електрона в атомі характеризується чотирма квантовими числами:

1) головне n=1,2,3... (будь-яке ціле);

2) азимутальне l=0,1,2,...,n–1 – всього n значень;

3) магнітне m_l= – l,...,0,...+l – всього 2l+1значень;

4) спінове m_s=±1/2 –всього два значення.

Енергія стану в основному визначається квантовими числами n і l. Крім того, має місце слабка залежність від m_l і m_s.

Заселення енергетичних рівній, тобто розподіл електронів по станам з різними значеннями енергії, підкоряється двом принципам.

1. Принцип Паулі. В одному і тому ж атомі не може бути двох електронів, що мають однакову сукупність чотирьох квантових чисел n, l, m_l, m_s.

2. Принцип мінімуму енергії. У незбудженому стані атома електрони повинні розташовуватися на самих низьких досяжних для них енергетичних рівнях.

Рис. 91

На рис. 91 наведено заселеність енергетичних рівнів літію (Z=5) у незбудженому стані (тобто з мінімумом енергії). Такий стан атома має назву основного стану. Рівні розв’язані (тобто відрізняються) по квантових числах n, l, m_l. Тоді на кожному рівні (тобто у стані зі заданою енергією) знаходиться по два електрони з протилежно орієнтованими спінами, оскільки спінове квантове число приймає тільки два значення m_s=±1/2. Сукупність електронів атома, що мають однакові квантові числа n і l, утворює оболонку. Кількість електронів у оболонці 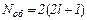. Сукупність оболонок з однаковими головними квантовими числами n утворює шар. Кількість електронів в шарі .

Розподіл електронів по оболонках і шарах. Цей розподіл, а також позначення шарів наведено у табл. 1.

З табл. 1 видно, що елементи із зарядовим числом Z=2 (Не) і Z=10 (Ne) мають повністю заповненні шари (К – шар для Не; K і L – шари для Ne). Тому їхні хімічні властивості подібні і обидва вони відносяться до однієї групи періодичної системи (групи інертних газів). Елементи із зарядовим числом Z=3 (Li) має повністю заповнений К-шар і один електрон у 2s стані. Елемент з Z=11 (Na) має повністю заповнені K і L шари і один електрон у 3s стані. Електрон 2S для Li і 3S для Na пов’язані з ядром слабше за інших і є валентними. У зв’язку з цим хімічні властивості Na і Li подібні і вони знаходяться в одній групі періодичних систем.

Таблиця 1

n	Кількість електронів у шарі	Умовна позначка шару	Кількість електронів у оболонці
			s(l=0)	p(l=1)	d(l=2)	f(l=3)	g(l=4)
		K		–	–	–	–
		L			–	–	–
		M				–	–
		N					–
		O

Таким чином, за допомогою табл. 1 всі хімічні елементи можна розташувати по групах періодичної системи елементів.

§7. Основні види міжатомного зв’язку молекул

Сили, що утримують атоми в молекулі, обумовлені взаємодією зовнішніх електронів атомів. Електрони внутрішніх оболонок при об’єднанні атомів у молекулу залишаються у попередніх станах. Розрізняють два види зв’язку атомів в молекулах.

1. Гомеополярний (або ковалентний) зв’язок. Він здійснюється в тих молекулах, в яких частина електронів рухається навколо обох ядер. Цей зв’язок утворюється парами електронів з протилежно орієнтованими спінами (див. рис. 92)

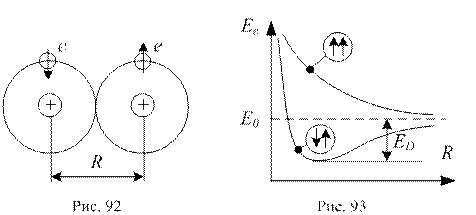
Та обставина, що утворення молекули можливе лише при наближенні атомів з антипаралельними спінами, пояснюється тим, що електронна енергія E_e , тобто енергія електронної конфігурації, залежить від відстані R між ядрами атомів у молекулі, притому у випадках паралельної і антипаралельної орієнтації спінів характер цієї залежності суттєво різний. На рис. 93 наведено такі залежності для молекул водню (Н₂).

Тільки при антипаралельній орієнтації спінів атомів у цієї залежності є мінімум і, отже, можливе утворення молекули, бо стійким станом є стан з мінімумом енергії. Граничне значення енергії Е₀ при , для обох кривих на рис. 93 однакове і дорівнює сумі енергії ізольованих атомів. Величина Е_D – є енергія зв’язку молекули. Вона дорівнює енергії, яку потрібно надати молекулі, щоб викликати її розподіл на атоми.

Рис. 94

2. Гетерополярний (або іонний) зв’язок. Він має місце, коли електрони в молекулі можна розділити на дві групи, кожна з яких весь час знаходиться коло одного з ядер. Електрони розподіляються так, що навколо одного з ядер утворюється надлишок електронів, а навколо іншого – їх нестача (див. рис. 94). Таким чином, молекула мовби складається з двох іонів протилежних знаків, які притягаються один до одного. Прикладами молекул з гетерополярним зв’язком є молекули NaCl, HCl та ін.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Теплове випромінювання	\|	КОНСПЕКТ ЛЕКЦІЙ

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.012 сек.