Основні поняття теорії графів

Граф - це форма задання відношень. Граф - графічна структура, яка складається з множини елементів, що називається вершинами і множини відношень між цими елементами, які позначаються в цій структурі лініями, що називаються ребрами або дугами.

Граф позначається буквою G, множина вершин V, множина відношень (дуг або ребер) – E, упорядкована пара G = (V, E). Нехай V = {v₁, v₂, ..., v_n} і E = = {e₁, e₂...,e_m}

При цьому елементи множини V зображають крапками на площині, а ребра (v_i, v_j ) — відрізками (прямолінійними або криволінійними), які з'єднують крапки v_i та v_j. Граф називається скінченним, якщо множини його вершин і ребер є скінченними. Кількість вершин графа n, а кількість ребер m. Граф, який містить n вершин та m ребер називають (n, m) - графом.

Кількість вершин n(G) графа називають його порядком.

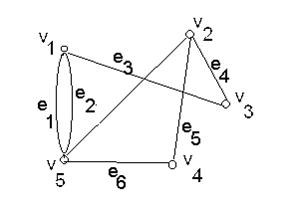
Рис. 2.

Граф, який є моделлю симетричного відношення називається простим або симетричним графом, неорієнтованим графом.

Граф G = (V, E), V = {v₁, v₂, v₃ v₄,, v₅} і E = {e₁, e₂, e₃, e₄, e₅, e₆}. Ребра можуть задаватися ще послідовністю вершин E = {(v₁, v₅), (v₁, v₅), (v₁, v₃), (v₂,,v₃),(v₂,v₄), (v₂, v₅), (v₄, v₅)}.

Граф, який показує наявність декількох відношень між однією і тією ж множиною елементів називається мультиграфом.

Основна ознака мультиграфа – між деякими його вершинами існує декілька ребер або дуг.

Граф, який є моделлю несиметричного відношення називається орієнтованим графом. Щоб змоделювати несиметричне відношення треба вказати направлення ребер. Направлення показують стрілочкою. Стрілочка, яка відображає несиметричне відношення називається дугою графа.

Рис. 3.

Таким чином для простого графа – граф складається з двох множин (вершин та ребер), для несиметричного графа – граф складається з двох множин (вершин та дуг).

Два ребра називаються суміжними, якщо обидва вони є інцидентними одній вершині.

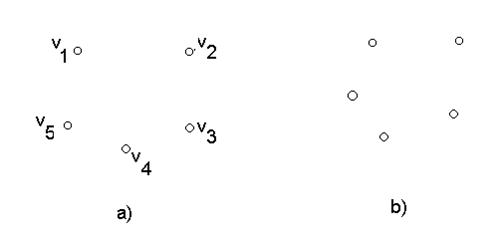
Рис. 4.

Якщо граф G = (V, Æ ) - множина відношень порожня (рис. 4, а).

Але якщо множина вершин V - порожня, то порожньою є також множина Е. Такий граф називається порожнім. Такий граф називається нуль-графом і позначається Æ (рис. 4, b).

Лінії, що зображають ребра графа, можуть перетинатися, але точки перетину не є вершинами; різні ребра можуть бути інцидентними одній і тій самій парі вершин (рис.2), такі ребра називаються кратними. Цей випадок відповідає наявності кількох однакових пар E = {(v₁, v₅), (v₁, v₅). Граф, що містить кратні ребра, називається мультиграфом.

Ребро може з'єднувати деяку вершину саму з собою (рис. 5), таке ребро називається петлею. Цей випадок відповідає наявності в множині Е пар вигляду (v, v). Граф із петлями та кратними ребрами називається псевдографом.

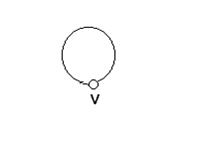
Рис. 5

Графи, які найчастіше розглядаються, є скінченними, тобто скінченні множини їхніх елементів (вершин і ребер), їх і розглядатимемо. Проте деякі поняття та результати, про які йтиметься, належать до довільних графів. Скінченний неорієнтований граф без петель і кратних ребер називається звичайним..

При зображенні орієнтованих графів напрямки ребер позначаються стрілками (рис. 3). Орієнтований граф може мати кратні ребра, петлі, а також петлі, що з'єднують ті ж самі вершини ребра, але у зворотних напрямках.

Є специфічний вид ребра або дуги, які і в симетричному і в орієнтованому називається однаково петля - модель рефлексивного відношення

Рис. 6.

Повний граф G = (V, E), n =_, m = _ .

Кожне ребро e_k Î E з’єднує пару вершин v_i_,v_j Î V, які є його кінцями ці вершини граничні. Розрізняють початкову вершину з якої дуга виходить та кінцеву вершину , в яку дуга входить. Дві вершини (граничні вершини) які з’єднані двома або більше ребрами називаються кратними.

В загальному випадку граф може містити і ізольовані вершини які не є граничними вершинами ні з одним з ребер.

Кожному неорієнтованому графу можна поставити у відповідність орієнтований граф з тією самою множиною вершин, в якій кожне ребро замінено двома орієнтованими ребрами, що є інцидентними тим самим вершинам і мають зворотні напрямки. Таку відповідь будемо називати канонічною.

Граф, що має як ребра, так і дуги, називається мішаним.

Інцидентність. Задання графа за допомогою матриці інцидентності.

Задати граф означає задати множини його вершин і ребер, а також відношення інцидентності. Коли граф G — скінченний, тоді вершини даного графа v₁ ,v₂,,..., v_n, а його ребра е₁, е₂,..., е_m. Відношення інцидентності можна означити матрицею S= _, що має n рядків й т стовпців. Рядки відповідають вершинам графа, а стовпці відповідають його ребрам. Якщо вершина v_i є інцидентною ребру е_о, , то s_ij = 1, в іншому випадку s_ij = 0. Це матриця інцидентності звичайного графа G, яка є одним із способів його визначення (для графа на рис. 2).

S_ij = _

;

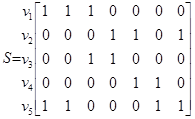У матриці інцидентності _ орієнтованого графа G, якщо вершина v_i —початок ребра e_j, то s_ij = 1; якщо v_i: - кінець e_j, то s_ij = -1. Кількість одиниць у рідку дорівнює степені відповідній вершині (для орграфа кількість позитивних одиниць визначає позитивну степінь, а кількість від’ємних одиниць - від’ємну степінь). Нульовий рядок відповідає ізольованій вершині, а нульовий стовпець - петлі.

Треба мати на увазі, що нульовий стовпець матриці інцидентності лише вказує на присутність петлі, але не містить відомостей про те, з якою вершиною зв’язана ця петля.

S_ij = _

S_ij = _.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Однорідні системи лінійних алгебраїчних рівнянь.	\|	Властивості матриці інцидентності

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.007 сек.