
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Округлення числа.
При округлені числа а його заміняють числом а1 з меншою кількістю значущих цифр. При округленні до m "значущих цифр" відкидають всі цифри, які стоять праворуч m-ої значущої цифри. Якщо перша зліва із відкинутих цифр більша або дорівнює 5, то останню цифру, яку залишають збільшують на 1.
Приклад: Вкажіть вірні цифри:


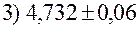
4. Відносна похибка наближеного значення числа.
Відносною похибкою  наближеного значення числа а називається відношення абсолютної похибки α цього наближення
наближеного значення числа а називається відношення абсолютної похибки α цього наближення
до числа а, тобто 
На практиці оцінюють модуль відносної похибки число Е, для якого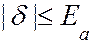 . Число Е називається границею відносної похибки
. Число Е називається границею відносної похибки
і визначається: 
Залежність відносної похибки від числа значущих цифр приведена в таблиці 1.
| Число | Най - | Найбі - | Границя абсолютної | Відносна похибка найменшого числа | Відносна похибка найбільшого числа |
| Однозначне | 0,5 | 0,5 = 50% | 0,056 = 5,6% | ||
| Двозначне | 0,5 | 0,05 = 5% | 0,005 = 0,5% | ||
| Тризначне | 0,5 | 0,005 = 0,5% | 0,0005 = 0,05% | ||
| Чотиризначне | 0,5 | 0,0005 = 0,05% | 0,00005 = 0,005% |
Із таблиці видно, що три вірні значущі цифри забезпечують точність результатів від 0,005 до 0,5%. В технічних розрахунках прийнято виконувати обчислення з трьома значущими цифрами. Границю абсолютної похибки знаходять по даній відносній похибці і модуль наближеного значення величини 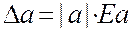
Приклад 1.
Знайти відносну похибку числа 6,8, якщо обидві цифри вірні.
По умові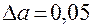 , а тому
, а тому 
Приклад 2.
Які цифри числа 4,83 (0,3%) вірні?
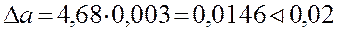

Вірні цифри 4,8
5. Дії над наближеними значеннями чисел.
а) Без врахування похибок.
При додаванні (відніманні) наближених значень чисел в результаті слід залишити стільки десяткових знаків, скільки їх має дане з найменшим числом десяткових знаків.
При множенні ( діленні)наближених значень чисел в результаті слід залишити стільки значущих цифр, скільки їх має дане з найменшим числом значущих цифр.
При піднесенні до степеня наближеного значення числа в результаті слід залишити стільки значущих цифр, скільки їх має основа степеня.
При додаванні кореня з наближеного значення числа в результаті слід залишити стільки значущих цифр, скільки їх має підкореневий вираз.
б) З урахуванням похибок.
Границя абсолютної похибки суми наближених значень чисел дорівнює сумі границь абсолютних похибок цих чисел
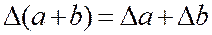

Границя абсолютної похибки різниці двох наближених значень чисел дорівнює сумі границь їх абсолютних похибок.

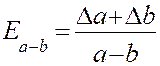
Границя відносної похибки добутку наближених значень чисел дорівнює сумі границь їх абсолютних похибок

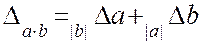
Границя відносної похибки частки наближених значень двох чисел дорівнює сумі границь їх абсолютних похибок
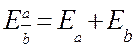
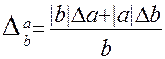
Границя відносної похибки степеня наближеного значення числа дорівнює добутку показника степеня на границю відносної похибки основи степеня


Границя відносної похибки кореня з наближеного значення числа дорівнює границі відносної похибки підкореневого числа поділеного на показник кореня

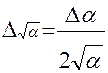

6. Обчислення з наперед заданою точністю.
Обернена задача:
Які повинні бути похибки даних наближених чисел, щоб в результаті обчислень була одержана наперед задана допустима границя похибки.
Приклад.
З якою точністю треба виміряти сторону квадрата, щоб при обчисленні площі границя абсолютної похибки не перевищувала
1 см2:

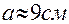
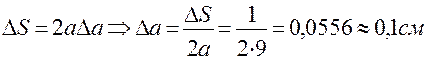
2. Дійсні числа.
1. Ірраціональні числа
Числа, які вживаються при лічбі, називаються натуральними
N = {1,2,3…}.
Множина нескінченна, дискретна. Завжди виконуються дії додавання і множення.
Приєднуємо до натуральних чисел число 0 і від’ємні числа. Утворюється множина цілих чисел Z. В множині Z завжди виконуються дії додавання, множення і віднімання.
Приєднуємо до множини цілих чисел дробові числа ( як додатні, так і від’ємні). Утворюється множина раціональних чисел Q.
Означення: Числа виду  , де
, де  ,
,  - називаються раціональними.
- називаються раціональними.
Властивості:
1) Для любих чисел a і b означена сума 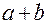 і операція суми комутативна і асоціативна:
і операція суми комутативна і асоціативна:


 2) Для любих чисел
2) Для любих чисел 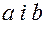 означений добуток
означений добуток 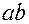 з властивостями:
з властивостями:


Любе раціональне число можна записати в вигляді нескінченного, десяткового дробу.
2. Ірраціональні числа.
Теорема.
Не існує раціонального числа, квадрата якого дорівнює 2.
Доведення.
Припустимо, що існує раціональне число  таке, що
таке, що  ,
, 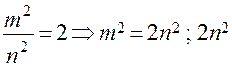 - парне число, а значить m2 – парне число. Тобто m = 2k. Маємо
- парне число, а значить m2 – парне число. Тобто m = 2k. Маємо  . Аналогічно: n – парне число. Значить дріб
. Аналогічно: n – парне число. Значить дріб  можна скоротити, що суперечить умові.
можна скоротити, що суперечить умові.
Таким чином, виникає необхідність ввести нові числа.
Ірраціональними числами називаються числа, які можна записати в вигляді десяткових нескінченних неперіодичних дробів – 1.
3. Дійсні числа.
Об’єднання раціональних і ірраціональних чисел називається дійсними числами – R.
Між множиною R всіх дійсних чисел і множиною всіх точок координатної прямої існує взаємно однозначна відповідність.
Числові проміжки:
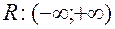 - числова вісь
- числова вісь
Якщо 
Якщо
Якщо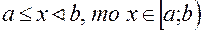
Якщо
Якщо 
3. Поняття функції, властивості.
Співвідношення між множинами x і y при якому кожному елементу x відповідає тільки один елемент y – множини.
Функція, яка задана на числовій множині і приймає значення із числової множини, називається числовою.
Множина x називається областю визначення функції D(x),а елементи цієї множини називається аргументами.
Множина y називається областю значення функції E(y), а елементи цієї множини називається функціями.
Задати числову функцію це значить:
1) Вказати D(x);
2) Вказати закон по якому кожному елементу x відповідає тільки один y.
Способи задавання функції:
1) З допомогою стрілок;
2) З допомогою впорядкованих пар;
3) Табличний;
4) Графічний;
5) Описовий;
6) Аналітичний;
7) Символічний.
Основні властивості функції
1) Монотонність – функція яка тільки зростає. Функція називається монотонно зростаючою якщо: для 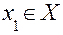 , для
, для 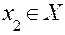 , із того, що
, із того, що 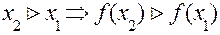 .
.
Функція називається монотонно спадною якщо: для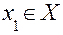 , для
, для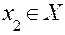 , із того, що
, із того, що 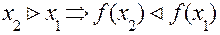 .
.
Функція, яка зростає і спадає, називається Кусково монотонною.
2) Парна і непарна функція.
Функція називається парною, якщо x – симетричнамножина і 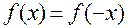
Функція називається непарною, якщо
3) Функція називається обмеженою, якщо її значення y не обмежене. Функція називається обмеженою, якщо її множина y обмежена.
4) Функція називається обмеженою, якщо кожному x відповідає один y і кожному y відповідає один x.
5) Функція називається періодичною, якщо існує таке найменше число T, яке будучи доданим до аргументу, значення функція не міняє.
6) Функція називається неперервною в точці  , якщо границя функції в цій точці існує і дорівнює значенню функції в цій точці
, якщо границя функції в цій точці існує і дорівнює значенню функції в цій точці  .
.
4. Графік функції.
Графіком функції називається множини точок площини  , де x приймає значення із D(x), а y – із E(y) функції.
, де x приймає значення із D(x), а y – із E(y) функції.
1) Графік лінійної функції 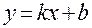 - пряма лінія.
- пряма лінія.
2) Графік функції 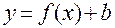 отримуємо із графіка
отримуємо із графіка 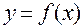 зміщенням його вздовж осі
зміщенням його вздовж осі  на
на 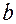 одиниць. Якщо
одиниць. Якщо 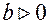 - вгору, а якщо
- вгору, а якщо  - вниз.
- вниз.
3) Графік функції 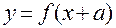 отримаємо із графіка
отримаємо із графіка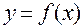 зміщенням його вздовж осі
зміщенням його вздовж осі 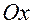 на
на 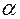 одиниць: якщо
одиниць: якщо - вліво, а якщо
- вліво, а якщо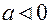 - вправо.
- вправо.
4) Графік функції  є композиція графіків 2) і 3).
є композиція графіків 2) і 3).
5)  Вершина
Вершина  . Будуємо відносно вершини
. Будуємо відносно вершини 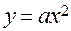
6) Графік функції 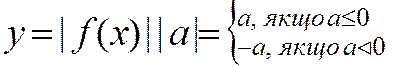
5) Графік функції 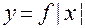 :
:
1) Будуємо 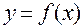 ;
;
2) Залишаємо ту частину графіка, яка знаходиться праворуч від осі  і дзеркально відображаємо відносно осі
і дзеркально відображаємо відносно осі  .
.
5. Приріст аргументу і приріст функції.
Якщо змінна величина х приймає значення від х1, до х2, то різниця між її значеннями називається приростом аргументу і позначається  .
.
Різниця між відповідними значеннями функції називається приростом функції і позначається  .
.
В загальному вигляді приріст функції в точці 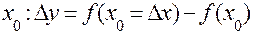 .
.
Геометричне приріст аргументу відповідає приросту абсциси точки кривої, а приріст функції – приросту ординати цієї точки.
6. Границя функції в точці і на нескінченності.
Число А називається границею функції 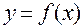 в точці
в точці 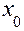 , якщо для будь-якого числа
, якщо для будь-якого числа 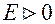 існує таке число
існує таке число 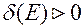 , що для всіх
, що для всіх  , і таких, що
, і таких, що  , виконується нерівність
, виконується нерівність 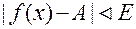 .
. 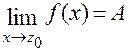 або
або .
.
Число А називається границею функції 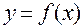 при
при 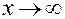 , якщо для любого
, якщо для любого 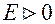 існує число
існує число 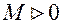 , що при всіх
, що при всіх  .
.
Функція  називається нескінченно малою, якщо
називається нескінченно малою, якщо  .
.
Функція  називається нескінченно великою, якщо
називається нескінченно великою, якщо 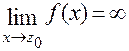 .
.
Якщо  - нескінченно мала, то
- нескінченно мала, то  нескінченно велика.
нескінченно велика.
7. Теорема про границі.
Якщо функції  і
і 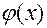 в точці
в точці 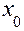 мають границі, то:
мають границі, то:
1) Границя суми дорівнює сумі границь 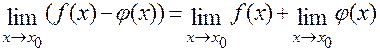 .
.
2) Границя добутку дорівнює добутку границь 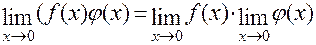 .
.
Наслідок 1. Постійний множник можна виносити за знак границі 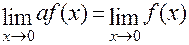 .
.
Наслідок 2. Границя степені дорівнює степені границь  .
.
3) Границя частки дорівнює частці границі 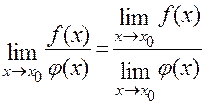 , при умові
, при умові  .
.
8. Неперервність функції в точці і на проміжку.
Функція називається неперервною в точці  , якщо границя функції в цій точці існує і дорівнює значенню функції в цій точці
, якщо границя функції в цій точці існує і дорівнює значенню функції в цій точці  .
.
Умови неперервності функції в точці:
1. Границя функції 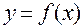 в точці
в точці  визначена.
визначена.
2. Границя функції 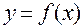 в точці
в точці  існує.
існує.
3. Границя дорівнює значенню функції в цій точці.
Функція називається неперервною проміжку, якщо вона неперервна в кожній точці цього проміжку.
Властивості неперервних функцій:
1. Многочлен є функція неперервна на всій числовій осі.
2. Дробово – раціональна функція є функція неперервна на області визначення.
3. Якщо функція  неперервна на сегменті
неперервна на сегменті 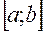 , то вона на цьому сегменті обмежена.
, то вона на цьому сегменті обмежена.
4. Якщо функція  неперервна на сегменті
неперервна на сегменті 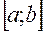 , то вона на цьому сегменті приймає найменше і найбільше значення.
, то вона на цьому сегменті приймає найменше і найбільше значення.
5. Якщо функція  непевна на сегменті
непевна на сегменті 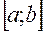 і на його кінцях приймає значення різних знаків, то існує хоч би одна точка С на
і на його кінцях приймає значення різних знаків, то існує хоч би одна точка С на 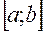 , в якій
, в якій 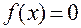 .
.
9. Застосування неперервності функції до наближених методів розв’язування рівнянь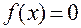 .
.
Метод половинного ділення.
Вважаємо, що графічним методом корені рівняння відокремлені і один із них (находиться на 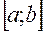 .
.
Задача полягає в тому, щоб обчислити корінь з заданою точністю . Для цього ділимо відрізок 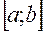 навпіл і обчислюємо значення функції
навпіл і обчислюємо значення функції  в середині відрізка
в середині відрізка 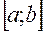 . Якщо
. Якщо 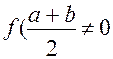 то для подальших обчислень вибирається один із отриманих половинок, на кінцях якої
то для подальших обчислень вибирається один із отриманих половинок, на кінцях якої приймає значення різних знаків. Повторюючи аналогічні обчислення, будемо все більш ближче наближатися до кореня рівняння
приймає значення різних знаків. Повторюючи аналогічні обчислення, будемо все більш ближче наближатися до кореня рівняння 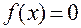 . Процес обчислення триватиме доти, доки довжина відрізка буде менше . Тоді за величину кореня, як правило, вибирають середину відрізка.
. Процес обчислення триватиме доти, доки довжина відрізка буде менше . Тоді за величину кореня, як правило, вибирають середину відрізка.
10. Комплексні числа.
1. Розширення множин дійсних чисел.
Відповідно до прийнятих в математиці принципів розширення поняття числа при розширенні множини дійсних чисел мають задовольнятися такі вимоги:
1. Означення нових чисел мусить спиратися на поняття дійсного числа, і нова множина має містити всі дійсні числа;
2. Для нових чисел повинні виконуватися п’ять законів прямих арифметичних лій;
3. У новій числовій множині мусить мати розв’язок рівняння 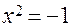 , бо в цій множині має виконуватися дія обернена до піднесення до степеня.
, бо в цій множині має виконуватися дія обернена до піднесення до степеня.
Число і квадрат якого дорівнює 1, позначається буквою і і називається уявною одиницею.
Рівність приймається за означенням і не доводиться. До нової множини належать числа ві – уявні числа.
Означення.
Всі числа виду а + ві, де а і в дійсні числа, а і уявна одиниця, називаються комплексними числами. «Комплексний» - складений. Числа а + ві ототожнюються з дійсними числами, тобто попередній числовий «запас» входить до нової числової множини як її частина.
Умови рівності комплексних чисел і правила виконання прямих дій:
1. Два комплексних числа а + ві і с + dі рівні між собою тоді і тільки тоді, коли а = с; b = d.
Числа а + ві і а – ві називаються спряженими.
2. Сумою двох комплексних чисел а + ві і с +dі називається комплексне число (а + с) + (b + d)і.
Додавання комплексних чисел підлягає переставному і сполучному закону 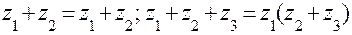 .
.
3. Добутком двох комплексних чисел а + ві і с +dі називається комплексне число (ас - bd) + (аd + bс) і.
4. Дія множення комплексних чисел підлягає переставному і сполучному закону. 
2. Геометрична інтерпретація комплексних чисел.

Кожному комплексному числу а + ві відповідає точка координатної площини М(а;в).
Координатну площину називають комплексною віссю абсцис – дійсною віссю, вісь ординат – уявною віссю.
Комплексне число можна інтерпретувати як вектор  .
.
Читайте також:
- Додатні ірраціональні числа. Невід’ємні дійсні числа.
- Іменникова категорія числа. Експресивна та інформативна функції іменників, ужитих в однині чи множині.
- Квантові числа.
- Ознаки подільності на складені числа.
- Поняття натурального ряду чисел та його відрізка. Лічба елементів скінченої множини. Порядкові і кількісні натуральні числа.
- Прості і складені числа. Нескінченність множини простих чисел. Решето Ератосфена.
- Теореми про подільність суми, різниці і добутку цілих невід’ємних чисел на натуральні числа.
| <== попередня сторінка | | | наступна сторінка ==> |
| Абсолютна похибка наближеного | | | Тригонометрична форма запису комплексних чисел. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |