• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Додатні ірраціональні числа. Невід’ємні дійсні числа.

2. Ми вже розглянули звичайні та десяткові дроби та виявили, що між ними існує певний зв'язок, а саме: кожний десятковий дріб можна перетворити у звичайний; не кожний звичайний дріб можна перетворити у скінченний десятковий дріб (коли це не можна зробити?!). Як скінченні, так і нескінченні періодичні десяткові дроби належать до множини Q раціональних чисел, яку можна також називати множиною періодичних десяткових дробів. З іншого боку, розглядаючи процес вимірювання величин чи розв’язування рівнянь виду х²=а, ми отримуємо числа, які не є періодичними десятковими дробами. У вказаних випадках можуть з’являтися нескінченні неперіодичні десяткові дроби, наприклад: 0,10100100010000…, √2, √3,√5, π, е тощо. Отже, такі дроби ми можемо отримати при вимірюванні несумірних відрізків і при розв'язанні рівнянь виду х^2к=а, де а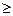0. Виявляється, що нескінченні неперіодичні десяткові дроби зображують числа, які не належать до множини раціональних чисел. Це числа нової природи. Таким чином, постає питання розширення множини раціональних чисел, яке слід провести, дотримуючись наступних умов:

- до множини раціональних чисел приєднаємо числа нової природи – ірраціональні числа;

- визначимо арифметичні операції додавання, віднімання, множення і ділення над ірраціональними числами так, щоб вони не суперечили правилам виконання дій над раціональними числами;

- поширимо основні закони (властивості) дій над раціональними числами на числа нової природи;

- поставимо завдання про можливість знаходження розв’язків рівняння виду хⁿ=а, де n і a - будь-які натуральні числа;

- поставимо вимогу про можливість знаходження спільної міри для будь-яких однорідних величин.

Для виконання поставлених завдань введемо означення понять, які відносяться до нової числової множини.

Означення: нескінченний неперіодичний десятковий дріб називається ірраціональним числом.

Прикладом таких чисел є наступні: Наприклад: Ö2,Ö3, p=3,141592…, 2,212212221… тощо. Хоча в означенні нічого не говориться про існування таких чисел, але, доводячи теорему про несумірність сторони квадрата з його діагоналлю, ми фактично довели теорему про існування ірраціональних чисел. Якщо до множини невід’ємних раціональних чисел ми приєднаємо додатні ірраціональні числа, то отримаємо множину невід’ємних дійсних чисел, яку прийнято позначати R₀. якщо ж розглянути ще й від’ємні ірраціональні числа, то матимемо справу з множиною дійсних чисел.

Означення: об'єднання множини Q раціональних чисел з множиною додатних і від'ємних ірраціональних чисел називають множиною дійсних чисел.

Множину дійсних чисел прийнято позначати R. Таким чином, можна записати таке співвідношення між відомими нам числовими множинами: RÉQÉZÉN або NÌZÌQÌR, яке можна зобразити за допомогою кругів Ейлера так, як це зроблено на діаграмі № 5.2.

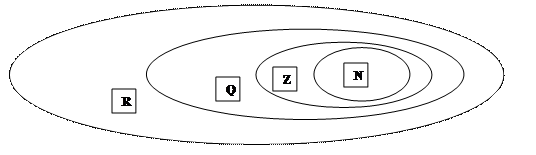
Діаграма № 5.2. Співвідношення між числовими множинами N, Z, Q, R.

Читайте також:

1. Дійсні типи
2. Дійсні типи
3. Дійсні числа
4. Додатні раціональні числа як нескінченні періодичні десяткові дроби. Чисті та мішані періодичні дроби та їх перетворення у звичайні.
5. Збирання матеріалу на основі спостережень за дійсністю
6. Іменникова категорія числа. Експресивна та інформативна функції іменників, ужитих в однині чи множині.
7. Квантові числа.
8. Мистецтво – це специфічний вид людської діяльності, що відображає навколишню дійсність і людську свідомість у художніх образах та є одним із засобів естетичного оволодіння світом.
9. Написати програму для обчислення значення функції f (0.8, a) + f (a, b)-f (2a-1, ab), де a, b дійсні числа і
10. Наука – сфера людської діяльності та одна з форм суспільної свідомості, функція якої – вироблення і теоретична систематизація об’єктивних знань про дійсність.
11. Невід’ємні раціональні числа та їх властивості.

Переглядів: 3746