
МАРК РЕГНЕРУС ДОСЛІДЖЕННЯ: Наскільки відрізняються діти, які виросли в одностатевих союзах
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
Контакти
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Невід’ємні раціональні числа та їх властивості.
3. Розширюючи множину цілих чисел, ми зазначали, що у новій числовій множині цілі числа повинні зберегтися. Для цього кожне ціле число буде позначати дробовим числом із знаменником 1. Наприклад, 0=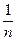 , 1=
, 1=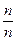 , 2=
, 2= тощо, де n – довільне ціле число. Тепер всі дроби можна розбити на класи, до кожного з яких входитимуть рівносильні дроби. Так, до першого класу віднесемо всі дроби рівносильні числу 0, до другого – рівносильні числу 1, тобто 1,
тощо, де n – довільне ціле число. Тепер всі дроби можна розбити на класи, до кожного з яких входитимуть рівносильні дроби. Так, до першого класу віднесемо всі дроби рівносильні числу 0, до другого – рівносильні числу 1, тобто 1,  , до наступного дроби, які дорівнюють
, до наступного дроби, які дорівнюють 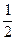 , тобто
, тобто 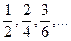 , тощо. Всі дроби кожного класу визначають одне й те ж саме дробове число. Серед множини цих чисел є одне особливе. Це нескоротний дріб.
, тощо. Всі дроби кожного класу визначають одне й те ж саме дробове число. Серед множини цих чисел є одне особливе. Це нескоротний дріб.
Означення: додатнім раціональним числом 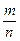 називається множина рівносильних йому дробів {
називається множина рівносильних йому дробів {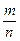 ,
,  ,
, 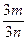 , …,
, …, 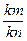 , …}.
, …}.
Так, наприклад дробовим числом  є множина рівносильних дробів
є множина рівносильних дробів 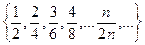 , дробовим числом
, дробовим числом  є множина рівносильних дробів
є множина рівносильних дробів 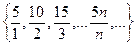 . У математиці доведено теорему, яку ми приймемо без доведення і яка вказує на існування та єдиність такого дробу.
. У математиці доведено теорему, яку ми приймемо без доведення і яка вказує на існування та єдиність такого дробу.
Теорема: для будь-якого додатного раціонального числа існує один і тільки один дріб, що його представляє, й такий, що чисельник і знаменник його взаємно-прості числа.
Означення: об’єднання множини невід’ємних цілих чисел та додатних дробів називають множиною невід’ємних раціональних чисел.
Символічно ця множина позначається так Q0. Перейдемо до розгляду властивостей цієї множини. Цілком зрозуміло, що в множині додатних раціональних чисел повинні зберегтися деякі властивості, що були в множині цілих чисел. Крім того, ця нова числова множина повинна мати і нові властивості, яких не було в попередній числовій множині.
Означення: числова множина називається щільною в собі, якщо між будь-якими її двома елементами міститься безліч елементів цієї множини.
Теорема:множина невід'ємних раціональних чисел щільна в собі.
Читайте також:
- Абсолютна величина числа позначається символом .
- Алгоритми арифметичних операцій над цілими невід’ємними числами у десятковій системі числення.
- Аналізатори людини та їхні властивості.
- Аналізатори людини та їхні властивості.
- Арифметичні операції над цілими числами
- Будова атомів та хімічний зв’язок між атомами визначають будову сполук, а отже і їх фізичні та хімічні властивості.
- Векторний добуток і його властивості.
- Визначення числа одиниць переносу
- Визначення числа прокладок
- Визначення. Числа й називаються комплексно спряженими.
- Відношення еквівалентності та порядку, їх властивості. Впорядковані множини. Зв'язок відношення еквівалентності з розбиттям множини на класи, що попарно не перетинаються.
- Власні і загальні іменники як лексико-граматичні розряди за специфікою виявлення категорії числа
| <== попередня сторінка | | | наступна сторінка ==> |
| Доведення. | | | Доведення. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |