• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Надійність системи

Однією із основних характеристик системи є її надійність. Надійність системи – це її здатність до безвідмовної роботи протягом заданого проміжку часу у визначених умовах.

Надійність системи відповідно до діючих стандартів - це комплексне поняття, що включає п’ять основних складових.

Працездатність – стан системи, при якому вона здатна виконувати задані функції з параметрами, що встановлені вимогами технічної документації.

Довговічність – це властивість системи зберігати працездатність при необхідних перервах на технічне обслуговування та поточний ремонт (ТО та ПР) до граничного стану, зазначеного в технічній документації.

Схоронність – властивість системи зберігати експлуатаційні показники в необхідних межах у період зберігання та транспортування.

Відновлюваність системи – це її властивість відновлювати працездатність у випадку виникнення відмови за допомогою ремонтів.

Ремонтопридатність – властивість системи, що полягає у пристосованості до попереджень, виявленню і ліквідації відмов та несправностей у процесі ТО та ПР.

Важливими поняттями в теорії надійності є ресурс, строк служби і ін.

Ресурсом називають тривалість функціонування або обсяг робіт, виконаний системою до граничного стану, який зазначено в технічній документації.

Строк служби – календарна тривалість експлуатації системи до граничного стану, який зазначено в технічній документації.

Різниця між ресурсом і строком служби обумовлена тим, що ресурс враховує фактичний наробіток системи, а строк служби – сумарну тривалість як роботи, так і простоїв.

У теорії надійності розрізняють два типи відмов – раптові та поступові. Раптова відмова – це миттєвий вихід з ладу у випадковий момент часу. Поступова відмова пов'язана з поступовим погіршенням характеристик системи, і як тільки параметри системи виходять за визначені межі, система вважається такою, що відмовила.

Розглянемо раптові відмови. Надійність системи при раптових відмовах залежить від складу і кількості елементів, що утворюють систему, від способу (структури) їхнього об'єднання у систему та від характеристик надійності кожного окремого елемента. Для оцінки надійності системи та її елементів існують кількісні характеристики.

Надійність елемента – це імовірність того, що даний елемент у даних умовах буде працювати безвідмовно протягом часу t, позначається 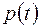. Функція 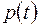– називається законом надійності. Природно, що при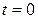 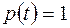, а при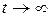 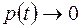тобто убуває.

Ненадійність елемента характеризується імовірністю 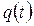того, що елемент відмовить протягом часу 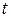, тобто 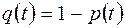(рис. 7.1).

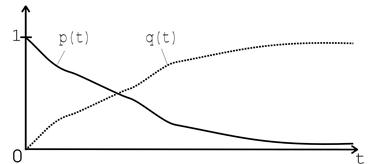
Рис. 7.1. Закон надійності 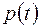і ненадійності .

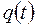Час 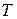безвідмовної роботи елемента є випадковою величиною, найважливішою характеристикою якої, є функція розподілу 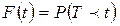, тобто 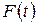- імовірність того, що за час 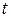елемент відмовить, тобто 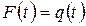, а 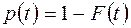, 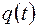– має властивості функції розподілу, 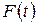–функція розподілу часу безвідмовної роботи.

На практиці зручніше використовувати щільність розподілу 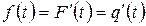. Щільність 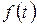визначається експериментально: спостерігається робота N однорідних елементів до моменту відмови 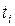. Формується масив 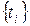і обробляється методами математичної статистики, тобто будується гістограма та вирівнюється аналітичною залежністю (рис. 7.2).

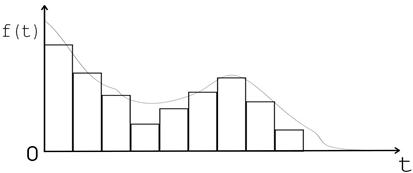
Рис. 7.2. Щільність розподілу .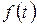

Характеристикою надійності елемента є середній час безвідмовної роботи .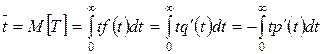

Інтегруючи вроздріб маємо: .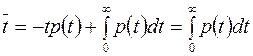

Для раптових відмов доцільно використовувати експоненційний закон 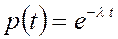, де й .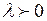

Функція розподілу часу безвідмовної роботи 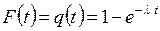, а 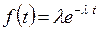, тобто потік відмов елементів представляє найпростіший потік з інтенсивністю .

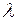Інтенсивність відмов 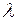– це середнє число відмов в одиницю часу, що приходиться на один працюючий елемент: .

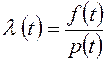Таким чином, основними кількісними характеристиками надійності 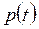є: імовірність безвідмовної роботи, інтенсивність відмов, середній час безвідмовної роботи, щільність розподілу часу безвідмовної роботи.

Розглянемо вплив структури системи S на її надійність. Надійність системи S, яка складається з n елементів, показники надійності яких відомі, залежить від того, як елементи об'єднані в систему, тобто від способу їх об‘єднання. Існує три основних способи об‘єднання елементів у систему: послідовний, паралельний і комбінований.

Якщо відмова елемента призводить до відмови всієї системи, то з точки зору надійності, такі елементи можна вважати об‘єднаними послідовно. Розглянемо надійність системи при такому способі об‘єднання елементів. Нехай P – надійність системи S, а P_i – надійності елементів Е_i (рис. 7.3)

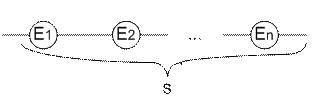
Рис. 7.3. Послідовне з’єднання елементів.

Нехай елементи відмовляють незалежно один від одного, тоді за правилом множення імовірностей незалежних подій маємо:

,

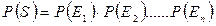або 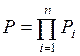. (9)

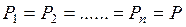Якщо , то .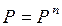

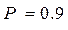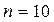Приклад: якщо , а , то .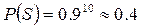

Таким чином, при послідовному способі об‘єднання елементів у системі надійність всієї системи S знижується.

Розглянемо cпосіб, при якому елементи включено в систему паралельно тим, надійність яких недостатня. Нехай елементи Е₁ і Е₂ незалежні по відмовах, а відповідні надійності (імовірності безвідмовної роботи) дорівнюють Р₁ і Р₂, знайдемо 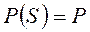(рис. 7.4).

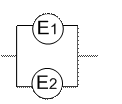
Рис. 7.4. Паралельне з’єднання елементів.

Розглянемо імовірність відмови системи 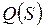. Щоб подія 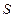(відмова всієї системи) відбулася, необхідно, щоб відмовили обидва елементи 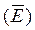, тобто за правилом множення імовірностей незалежних подій маємо:

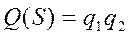, (10)

де 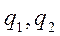– відповідні імовірності того, що елементи відмовлять, які визначаються як .

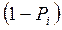Тоді маємо:

;

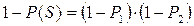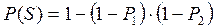. (11)

Якщо число дублюючих один одного незалежних елементів дорівнює n, то надійність системи 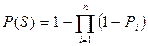, якщ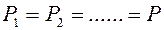о , то .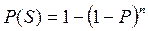

Для оцінки надійності складної структури, що включає в себе послідовні та паралельні об’єднання елементів (комбінований спосіб), доцільно поділити систему на ряд підсистем, що не мають загальних елементів. На рисунку 7.5 наведений приклад розбиття складної системи із семи елементів на підсистеми. Тут підсистема І містить два елементи, що пов’язані послідовно, підсистема ІІ – два паралельно зв’язаних елементи, підсистема ІІІ об’єднує послідовно І та ІІ підсистеми, IV підсистема – два паралельно зв’язаних елементи, V підсистема послідовно поєднує IV підсистему з п’ятим елементом.

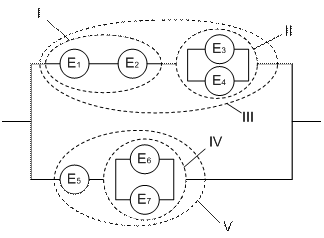
Рис. 7.5. Складна система з паралельними та послідовними зв’язками між елементами.

Відповідно отримуємо:

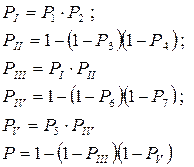(12)

Таким чином можна оцінити надійність складної системи при раптових відмовах.

Для характеристики надійності системи при поступових відмовах використовується так звана 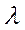характеристика (рис. 7.6). Відповідно до неї:

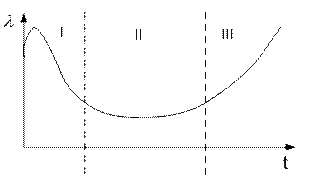
І – період приробітку;

ІІ - нормальної експлуатації;

ІІІ- зношування.

Рис. 7.6. Характеристика надійності системи при поступових відмовах.

У першому періоді (приробітку) щільність функції розподілу часу безвідмовної роботи підпорядкована розподілу Вейбулла. У цьому випадку щільність імовірності відмов визначається за формулою

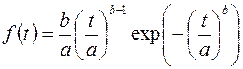, (13)

де 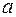та 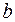– параметри розподілу. При 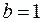розподіл трансформується у експоненційний закон, а при 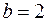– у закон розподілу Релея. Для періоду приробітку системи параметр 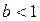. Імовірність безвідмовної роботи 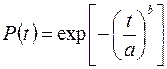, а інтенсивність відмов .

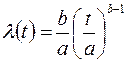У другому періоді 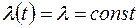, а імовірність відмов підкоряється експоненційному закону 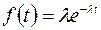, імовірність безвідмовної роботи .

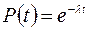У третьому періоді для характеристики надійності може бути використаний нормальний закон .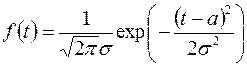

Ці характеристики надійності справедливі для неремонтуємих систем.

Ремонтуємі системи після відмов відновлюються шляхом проведення ремонтів.

Читайте також:

1. I. Органи і системи, що забезпечують функцію виділення
2. I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
3. II. Анатомічний склад лімфатичної системи
4. IV. Розподіл нервової системи
5. IV. Система зв’язків всередині центральної нервової системи
6. IV. Філогенез кровоносної системи
7. POS-системи
8. VI. Філогенез нервової системи
9. Автокореляційна характеристика системи
10. АВТОМАТИЗОВАНІ СИСТЕМИ ДИСПЕТЧЕРСЬКОГО УПРАВЛІННЯ
11. АВТОМАТИЗОВАНІ СИСТЕМИ УПРАВЛІННЯ ДОРОЖНІМ РУХОМ
12. Автоматизовані форми та системи обліку.

Переглядів: 5764