• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Втрати напору у трубах при турбулентному режимі руху рідини.

Механізм втрат напору (енергії) у ламінарному і турбулентному русі рідини істотно відрізняються. У ламінарному потоку втрати напору обумовлені виключно подоланням в’язкого тертя, які виникають між шарами рідини і пропорційні першій степені швидкості. Таким чином, джерелом втрат напору є сили внутрішнього тертя.

Інше положення спостерігається при турбулентному русі. Тут немає одноманітності з точки зору діючих сил у різних точках перерізу потоку. Тут діють сили внутрішнього тертя (ламінарний підшарок), сили в’язкості і сили інерції (перехідна зона), інерційні сили (турбулентне ядро).

У турбулентному режимі втрати напору обумовлені перемішуванням кінцевих мас рідини і появленням у зв’язку з цим додаткового напруження тертя, а тому втрати напору пропорційні квадрату швидкості.

З огляду складності турбулентної течії і важкості її аналітичного дослідження до теперішнього часу для неї не існує достатньо суворої та точної теорії. У більшості випадків для практичних розрахунків, пов’язаних з турбулентною течією рідини у трубах, використовуються експериментальні дані, які систематизовані на підґрунті теорії гідродинамічної подібності.

Основною формулою для розрахунку втрат напору при турбулентній течії у круглих трубах є емпірична формула, яка називається формулою Дарсі – Вейсбаха:

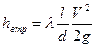
Теорія гідродинамічної подібності говорить про те, що l повинен бути функцією числа Re , а також може залежати від безрозмірного геометричного фактору 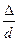, де D - шорсткість стінок.

Абсолютною шорсткістю D називають висоту нерівностей – виступів на внутрішніх поверхнях трубопроводу. Як правило, висота виступів шорсткості вздовж стінки не залишається постійною, а самі виступи мають різну форму, що істотно ускладнює облік впливу шорсткості на втрати напору. Тому з метою спрощення розрахунків вводять поняття еквівалентної шорсткості D_е, при якій втрати напору у трубі виходять такими ж, як і при фактично неоднорідній шорсткості.

Значення D_е для деяких труб складає: для нових тягнутих труб із скла і кольорових металів – 0,01…0,02 мм; для нових і чистих сталевих цільнотягнутих труб – 0,05 … 0,15 мм. Дані про шорсткість різноманітних труб зводяться в довідникові таблиці. При турбулентному режимі руху рідини шорсткість стінок істотно впливає на опір руху рідини, тому що сприяє турбулізації потоку.

Таким чином, коефіцієнт опору тертя l по довжині потоку залежить не тільки від в’язкості рідини, але і від шорсткості стінок, тобто .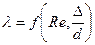

Тому правдивість розрахунку втрат енергії при турбулентному русі в багато чому залежить від правильного визначення коефіцієнту опору тертя по довжині потоку l. Дослідженням опору труб присвячено багато робіт. Однак до сих пір із-за складності турбулентної течії немає загального теоретичного методу визначення l для труб із різною шорсткістю при різній ступені турбулентизації потоку. Саме тому існує багато емпіричних формул для визначення l. Кожна з цих формул дійсна тільки для тих умов, при яких вона була одержана. Це дуже ускладнює вибір оптимального значення l для кожного конкретного випадку.

Перш ніж перейти до конкретного визначення залежностей для розрахунку коефіцієнта опору тертя l, розглянемо деякі дані, які були одержані відомим радянським вченим І. Нікурадзе. Він досліджував опір трубопроводів з рівномірною штучною зернистою шорсткістю, яка одержана шляхом наклеювання піщинок на внутрішню поверхню труб, а також обробив велику кількість даних про опір різноманітних трубопроводів при різних режимах і графічно надав відповідні залежності.

З даних, одержаних І. Нікурадзе (рис. 4), витікає, що залежність коефіцієнта опору тертя l по довжині від Re може бути розділена на чотири зони.

Перша зона, де значення l розташовані вздовж ділянки прямої 1 – 2, відноситься до ламінарного режиму. Тут l є функцією тільки числа Re і визначається залежністю 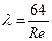. У другій зоні закономірності, яким підкоряється l, неодноманітні. Так, при Re > 2320 до Re » 4000, рух рідини характеризується складним законом гідравлічного опору. Втрати напору майже не залежать від шорсткості труб. Для цієї області течії величина коефіцієнта опору тертя може бути визначена залежністю, одержаною Н.З. Френкелем:

.

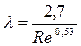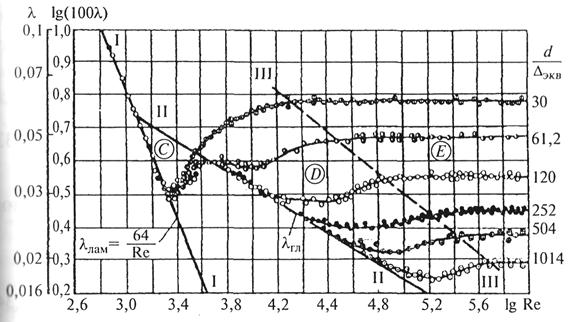
Рис. 4 Графік І. Нікурадзе – залежність 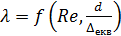для труб з однорідною рівнозерністою шорсткістю:

І – зона ламінарного режиму; ІІ – перехідна зона; ІІІ – зона турбулентного режиму; С – область гідравлічно гладких труб; D – зона до квадратичної області опору; Е – квадратична область опору.

При турбулентному режимі руху, коли Re > 4000, розрізняють зону гідравлічно гладких труб С, яка входить до другої. Для визначення l в межах цієї ділянки кривої можна користуватися формулами:

Блазіуса: при 4000 < Re < 10⁵

Колбрука – Конакова: 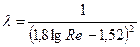при 4000 < Re < 10⁶.

Ці формули використовуються для розрахунку технічно гладких труб, до яких відносять скляні, цільнотянуті труби з кольорових металів (а також з алюмінієвих сплавів) та високоякісні безшовні сталеві труби. До технічно гладких труб відносять також паливопроводи та труби, які використовують у гідросистемах.

Зона D – доквадратичного опору. У цій області турбулентного руху для не цілком шорстких труб втрати напору визначаються числом Re і шорсткістю стінок труби.

Орієнтовано межі зони визначаються нерівністю:

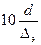< Re <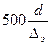

Численне значення D_е для труб із різноманітних матеріалів наводяться у довідковій літературі.

Для цієї області течії можна використовувати ряд залежностей:

формула Кольбрука:

формула А.Д. Альтшуля:

.

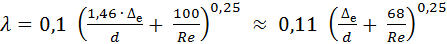Розглянемо зону Е, де опір пропорційний квадрату швидкості, тобто зону квадратичного опору, “цілком шорстких” труб. Нижньою межею зони є нерівність Re > 500 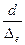(праворуч умовної лінії). Тут втрати напору і коефіцієнт опору тертя по довжині l залежать від гладкості 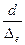, а від Re не залежать. Тому графіки, які визначають величину l для квадратного опору, являють собою прямі лінії, які паралельні осі абсцис.

Для визначення l у цій зоні запропоновані ряд формул. До найбільш відомих відносяться:

Прандтля – Нікурадзе:

,

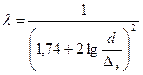Шифрінсона:

,

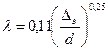Павловського та інші.

Дослідження показали, що квадратичний закон опору підтверджується далеко не в усіх випадках руху рідини. Однак формула Дарсі-Вейсбаха виявилась дуже зручною для практичних цілей і доцільною з точки зору одноманітності розрахунку і звичайно використовується як для ламінарного, так і для турбулентного режиму. Відхилення від квадратичного закону враховується тим, що значення коефіцієнту l ставиться у посередню залежність від швидкості.

Надалі внаслідок богаточисельних дослідів з технічними трубопроводами, тобто з трубами, шорсткість стінок яких обумовлювалась природними умовами, було виявлено наступне. По-перше, робочою для технічних трубопроводів є головним чином перехідна область опору. По-друге, закономірність зміни опору у перехідній області порівняно з трубами, які мають штучну шорсткість, носить зовсім інший характер: для технічних трубопроводів l зростає разом із зменшенням Re , при чому l має більш абсолютне значення.

Дослідження показали, що квадратичний закон опору підтверджується далеко не в усіх випадках руху рідини. Однак формула Дарсі-Вейсбаха виявилась дуже зручною для практичних цілей і доцільною з точки зору одноманітності розрахунку і звичайно використовується як для ламінарного, так і для турбулентного режиму. Відхилення від квадратичного закону враховуються тим, що значення коефіцієнту l ставиться у посередню залежність від швидкості.

Дослідження І. Нікурадзе з трубами, які мають стінки з штучною шорсткістю, показали наявність двох областей опору при турбулентному режимі: шорсткої та гладкої. Перехідна зона між шорстким та гладким тертям, де одночасно впливає як в’язкість рідини, так і шорсткість стінок, Л. Прандтлем і І. Нікурадзе не досліджувалась.

У ВТІ Г.А. Муріним були проведені і оброблені досліди по дослідженню труб різних сортаментів діаметром від 40 до 160 мм.

Результати дослідів надані графіком в межах Re = 4×10^-3 ¸ 4×10⁷. Тут чітко розрізняються три області опору при турбулентному режимі.

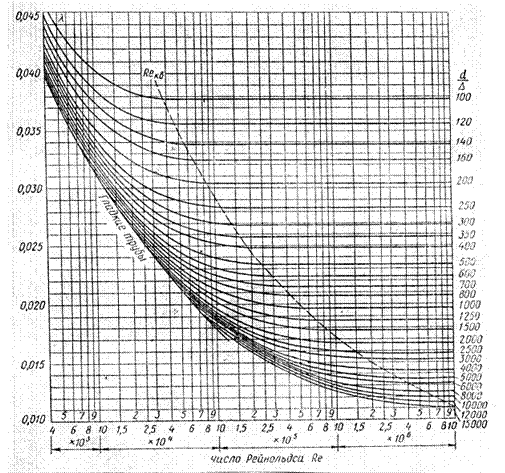Рис. 5 Графік Г.А. Муріна – залежність λ = f (Re, d/∆)

Область шорстких труб обмежена ліворуч штриховою лінією. Лінії l=f(Re) паралельні осі абсцис і коефіцієнт гідравлічного опору визначається тільки шорсткістю стінок труби. Перехідна область опору обмежується праворуч штриховою лінією, а ліворуч – огинаючою кривою. Значення l залежить не тільки від шорсткості, але і істотно зростає із зменшенням Re.

Порівніючи два графіка (Нікурадзе і Муріна) можно бачити, що вид кривих у зоні шерстких труб розрізняється, що пояснюється нерівномірністю шорсткості природних труб. При збільшенні числа Re у стиканні з турбулентним ядром вступають спочатку найбільш високі виступи, а потім поступово останні. Цим, як вважають, обумовлене плавне зниження ординат кривих у перехідних зонах. У області гідравлічно гладких труб l однозначно визначається числом Re.

Лекція № 8 «Гідравлічний удар в трубах»

1. Фізичні процеси виникнення гідравлічного удару.

2. Визначення ударного тиску.

3. Запобігання гідравлічного удару.

Читайте також:

1. Q6 розраховують тільки при нестаціонарному режимі
2. Бізнес-логістика в режимі INTERNET
3. Вибір режимів обробки заготовки різанням
4. Вибір схеми підключення абонентів залежно від режимів тиску.
5. Види втрат у підприємницькій діяльності.Безпосередньо з категорією ризику пов’язані такі поняття як витрати, втрати й збитки.
6. Визначення напору насоса при проектуванні
7. Вимоги до режимів праці і відпочинку та профілактичних медичних оглядів
8. Висота напору.
9. Вихрові струми. Втрати в сталі
10. Втрати в магнітопроводах
11. Втрати в трансформаторах
12. Втрати економіки від надмірного безробіття

Переглядів: 7430